11.14 : Structures des solides
Les solides dans lesquels les atomes, les ions ou les molécules sont disposés selon un motif répétitif défini sont appelés des solides cristallins. Les métaux et les composés ioniques forment généralement des solides cristallins ordonnés. Un solide cristallin a une température de fusion précise parce que chaque atome ou molécule du même type est maintenu en place avec les mêmes forces ou la même énergie. Les solides amorphes, ou solides non cristallins (ou parfois verres), qui n'ont pas de structure interne ordonnée et sont disposés de façon aléatoire. Les substances qui se composent de grandes molécules, ou d'un mélange de molécules dont les mouvements sont plus limités, forment souvent des solides amorphes. Le matériau amorphe devient mou progressivement, sur une plage de températures, en raison de la non-équivalence structurelle des molécules. Lorsqu'un matériau amorphe est chauffé, les attractions intermoléculaires les plus faibles sont rompues en premier. À mesure que la température augmente, des attractions plus fortes sont rompues.
Maille
La structure d'un solide cristallin est mieux décrite par son unité de répétition la plus simple, appelée maille. La maille est constituée des nœuds du réseau qui représentent les emplacements des atomes ou des ions. L'ensemble de la structure est alors constitué de cette maille qui se répète en trois dimensions, comme illustré dans la figure 1.
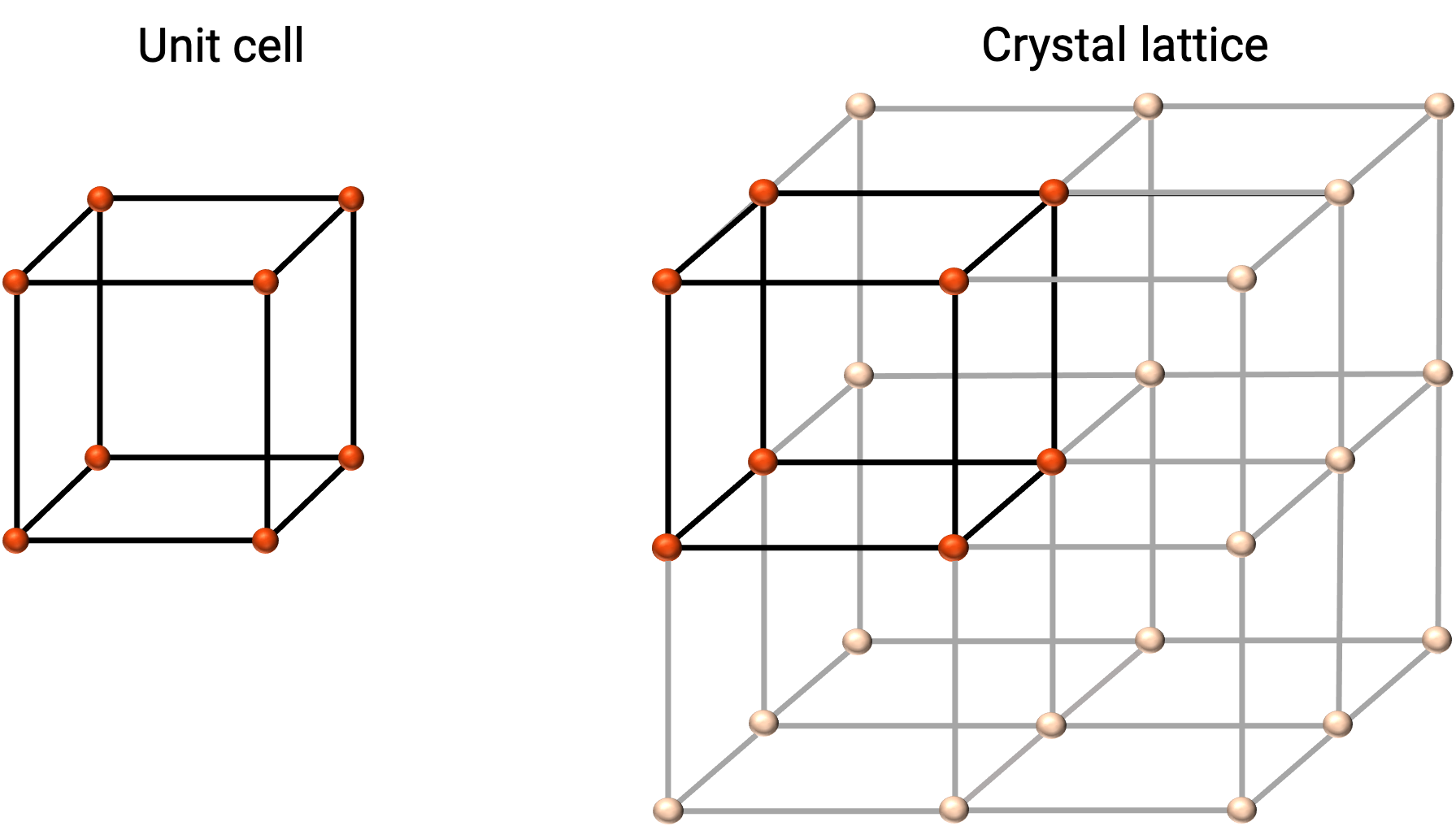
Figure 1. Maille et réseau cristallin avec les points du réseau indiqués en rouge.
En général, une maille est définie par les longueurs de trois axes (a, b et c) et les angles (α, β et γ) entre eux, comme illustré dans la figure 2. Les axes sont définis comme étant les longueurs entre les nœuds du réseau dans l'espace.
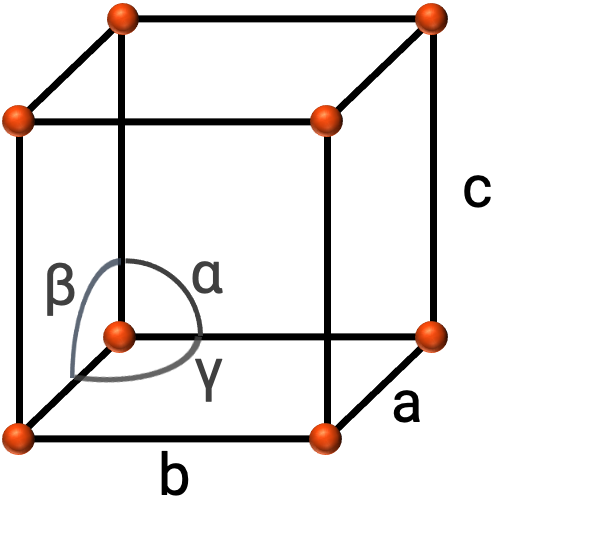
Figure 2. La maille est définie par ses axes (a, b et c) et ses angles (α, β, et γ)
Il existe sept systèmes de réseaux différents, dont certains ont plus d'un type de réseau, pour un total de quatorze mailles différentes.
| Systèmes | Angles | Axes |
| Cubique | α = β = γ = 90° | a = b = c |
| Tétragonal | α = β = γ = 90° | a = b ≠ c |
| Orthorhombique | α = β = γ = 90° | a ≠ b ≠ c |
| Monoclinique | α = γ = 90° ; β ≠ 90° | a ≠ b ≠ c |
| Triclinique | α ≠ β ≠ γ ≠ 90° | a ≠ b ≠ c |
Ce texte est adapté deOpenstax, Chimie 2e, Section 10.6 : Structures du réseau dans les solides cristallins.
Du chapitre 11:

Now Playing
11.14 : Structures des solides
Liquides, solides et forces intermoléculaires
14.0K Vues

11.1 : Comparaison moléculaire des gaz, liquides et solides
Liquides, solides et forces intermoléculaires
40.5K Vues

11.2 : Forces intermoléculaires vs intramoléculaires
Liquides, solides et forces intermoléculaires
86.5K Vues

11.3 : Forces intermoléculaires
Liquides, solides et forces intermoléculaires
57.7K Vues

11.4 : Comparaison des forces intermoléculaires : point de fusion, point d'ébullition et miscibilité
Liquides, solides et forces intermoléculaires
43.8K Vues

11.5 : Tension superficielle, capillarité et viscosité
Liquides, solides et forces intermoléculaires
27.5K Vues

11.6 : Changement d'état
Liquides, solides et forces intermoléculaires
18.8K Vues

11.7 : Changement d'état : vaporisation et condensation
Liquides, solides et forces intermoléculaires
17.2K Vues

11.8 : Pression de vapeur saturante
Liquides, solides et forces intermoléculaires
34.3K Vues

11.9 : Équation de Clausius-Clapeyron
Liquides, solides et forces intermoléculaires
55.9K Vues

11.10 : Changement d'état : fusion et congélation
Liquides, solides et forces intermoléculaires
12.3K Vues

11.11 : Changement d'état : sublimation et condensation solide
Liquides, solides et forces intermoléculaires
16.7K Vues

11.12 : Courbes de température de changement d'état
Liquides, solides et forces intermoléculaires
22.5K Vues

11.13 : Diagrammes de phases
Liquides, solides et forces intermoléculaires
39.7K Vues

11.15 : Solides moléculaires et ioniques
Liquides, solides et forces intermoléculaires
16.9K Vues
See More