Poco dopo che de Broglie pubblicò le sue idee secondo cui l'elettrone in un atomo di idrogeno poteva essere meglio considerato come un'onda circolare in piedi invece di una particella che si muoveva in orbite circolari quantizzate, Erwin Schrödinger estese il lavoro di de Broglie derivando quella che oggi è nota come equazione di Schrödinger. Quando Schrödinger applicava la sua equazione agli atomi simili all'idrogeno, fu in grado di riprodurre l'espressione di Bohr per l'energia e, quindi, la formula di Rydberg che governava gli spettri di idrogeno. Schrödinger descrisse gli elettroni come onde stazionarie tridimensionali, o funzioni d'onda, rappresentate dalla lettera greca psi, ψ.
Qualche anno dopo, Max Born propose un'interpretazione della funzione d'onda ψ che è ancora accettata oggi: gli elettroni sono ancora particelle, e quindi le onde rappresentate da ψ non sono onde fisiche ma, invece, sono complesse ampiezze di probabilità. Il quadrato della grandezza di una funzione d'onda â£ψâ£2 descrive la probabilità che la particella quantistica sia presente vicino a una certa posizione nello spazio. Ciò significa che le funzioni d'onda possono essere utilizzate per determinare la distribuzione della densità dell'elettrone rispetto al nucleo in un atomo. Nella forma più generale, l'equazione di Schrödinger può essere scritta come:
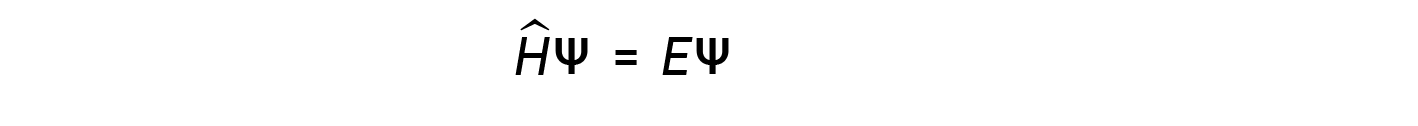
dove, Ĥ è l'operatore hamiltoniano, un insieme di operazioni matematiche che rappresentano l'energia totale (potenziale più cinetica) della particella quantistica (come un elettrone in un atomo), ψ è la funzione d'onda di questa particella che può essere utilizzata per trovare la distribuzione speciale della probabilità di trovare la particella, ed E è il valore effettivo dell'energia totale della particella.
Il lavoro di Schrödinger, così come quello di Heisenberg e di molti altri scienziati che seguono le loro orme, è generalmente indicato come meccanica quantistica.
Il modello meccanico quantistico descrive un orbitale come uno spazio tridimensionale attorno al nucleo all'interno di un atomo, dove la probabilità di trovare un elettrone è la più alta.
Questo testo è adattato da Openstax, Chemistry 2e, Section 6.3: Development of Quantum Theory.
Dal capitolo 7:

Now Playing
7.9 : Il modello quantistico-meccanico di un atomo
Struttura elettronica degli atomi
41.6K Visualizzazioni

7.1 : La natura ondulatoria della luce
Struttura elettronica degli atomi
48.0K Visualizzazioni

7.2 : Lo spettro elettromagnetico
Struttura elettronica degli atomi
52.3K Visualizzazioni

7.3 : Interferenza e diffrazione
Struttura elettronica degli atomi
30.2K Visualizzazioni

7.4 : Effetto fotoelettrico
Struttura elettronica degli atomi
29.1K Visualizzazioni

7.5 : Il modello di Bohr
Struttura elettronica degli atomi
49.6K Visualizzazioni

7.6 : Spettri di emissione
Struttura elettronica degli atomi
49.1K Visualizzazioni

7.7 : La lunghezza d'onda di de Broglie
Struttura elettronica degli atomi
25.2K Visualizzazioni

7.8 : Il principio dell'incertezza
Struttura elettronica degli atomi
22.8K Visualizzazioni

7.10 : Numeri quantistici
Struttura elettronica degli atomi
34.0K Visualizzazioni

7.11 : Orbitali atomici
Struttura elettronica degli atomi
32.8K Visualizzazioni

7.12 : Il principio di esclusione di Pauli
Struttura elettronica degli atomi
33.5K Visualizzazioni

7.13 : Le energie degli orbitali atomici
Struttura elettronica degli atomi
23.6K Visualizzazioni

7.14 : Il principio di Aufbau e la regola di Hund
Struttura elettronica degli atomi
42.9K Visualizzazioni

7.15 : Configurazione elettronica di atomi multielettronici
Struttura elettronica degli atomi
37.5K Visualizzazioni