È necessario avere un abbonamento a JoVE per visualizzare questo. Accedi o inizia la tua prova gratuita.
Method Article
Modellare l'ampiezza e la fase dei fasci Laser utilizzando un modulatore di luce spaziale sola fase
In questo articolo
Riepilogo
Vi mostriamo come codificare il campo complesso di raggi laser utilizzando un elemento monofase. Un interferometro di comune-percorso viene impiegato per mescolare le informazioni di fase visualizzate in un sola fase spaziale modulatore di luce finalmente recuperare il modello di campo complesso desiderato l'output di un sistema di imaging ottico.
Abstract
Lo scopo di questo articolo è dimostrare visivamente con l'utilizzo di un metodo interferometrico per codifica complessi campi associati alle radiazioni laser coerente. Il metodo si basa sulla somma coerente di due onde uniforme, precedentemente codificati in un sola fase modulatore luce spaziale (SLM) di multiplexing spaziale delle loro fasi. Qui, il processo di interferenza avviene applicando un filtro spaziale di frequenze di luce sul piano di Fourier di certo sistema di imaging. La corretta attuazione di questo metodo consente di arbitrario fase e ampiezza informazioni da recuperare l'output del sistema ottico.
È una tecnica di codifica in asse, piuttosto che fuori asse, con un algoritmo di elaborazione diretta (non un ciclo iterativo) e senza rumore coerente (macchiolina). Il campo complesso può essere Estratto esattamente l'output del sistema ottico, ad eccezione di qualche perdita di risoluzione a causa del processo di filtraggio di frequenza. La principale limitazione del metodo potrebbe venire dall'incapacità di operare a tassi di frequenza superiore alla frequenza di aggiornamento di SLM. Le applicazioni includono, ma non sono limitate a, microscopia lineare e non lineari, formazione del fascio o micro-lavorazione laser di superfici di materiale.
Introduzione
Quasi tutte le applicazioni laser sono in stretta relazione con la gestione del fronte d'onda ottico della luce. Nell'approssimazione parassiale, campo complesso connesso con la radiazione laser può essere descritto da due termini, l'ampiezza e la fase. Avere il controllo su questi due termini è necessaria per modificare il temporale e la struttura spaziale dei fasci laser a volontà. In generale, l'ampiezza e la fase di un fascio laser può essere correttamente modificati con vari metodi, compreso l'uso di componenti ottici che vanno da lenti di massa singola, beam splitter e specchi a dispositivi più complessi come specchi deformabili o luce spaziale modulatori. Qui, vi mostriamo un metodo per la codifica e ricostruendo il campo complesso di fasci laser coerente, che si basa sulla teoria di ologramma di doppio-fase1e l'utilizzo di un interferometro di comune-percorso.
Al giorno d'oggi, esiste una vasta gamma di metodi per codificare i campi complessi di laser travi2,3,4,5. In questo contesto, alcuni metodi consolidati per produrre modulazione di ampiezza e fase si basano sull'uso di ologrammi digitale6. Un punto comune a tutti questi metodi è la necessità di generare un offset spaziale per separare il fascio di output desiderato dall'ordine dello zeroth provenienti dalla riflessione della luce sul display SLM. Questi metodi sono fondamentalmente fuori asse (solitamente l'applicazione per il primo ordine di diffrazione della grata), che impiegano grata di fase non solo per codificare la fase, ma anche di introdurre la necessaria modulazione di ampiezza. In particolare, la modulazione di ampiezza viene eseguita da spazialmente abbassando l'altezza della grata, che chiaramente si riduce l'efficienza di diffrazione. Il processo di ricostruzione di ologramma ottiene principalmente una ricostruzione approssimativa, ma non esatta, dell'ampiezza e fase del complesso campo desiderato. Discrepanze tra teoria ed esperimento sembrano apparire da un'imprecisa codifica le informazioni di ampiezza, nonché altri problemi sperimentali accadendo durante il filtraggio spaziale del primo ordine di diffrazione o a causa di effetti pixilation SLM. Inoltre, il profilo di intensità del fascio luminoso ingresso può introdurre restrizioni la potenza in uscita.
Al contrario, con il metodo introdotto7, tutti i gestione della luce avviene lungo l'asse, che è molto conveniente da un punto di vista sperimentale. Inoltre, essa si avvale di considerare, nell'approssimazione parassiale, campo complesso associato con raggi laser come una somma di due onde uniforme. Le informazioni di ampiezza sono sintetizzato tramite l'interferenza di queste onde uniforme. In pratica, tale interferenza avviene tramite filtro spaziale di frequenze di luce sul piano di Fourier di un determinato sistema di imaging. In precedenza, i modelli di fase connessi con le onde uniforme nello spazio sono multiplexati e codificati in una sola fase SLM (posizionato sul piano di ingresso di questo sistema di imaging). Quindi, l'installazione tutto ottico può essere considerato come un interferometro di comune-percorso (molto robusto contro le vibrazioni meccaniche, cambiamenti di temperatura o disallineamenti ottici). Si prega di notare che il processo di interferenza di cui sopra può essere realizzato in alternativa utilizzando altri layout ottico: con un paio di sola fase slm posizionato correttamente all'interno di un tipico interferometro di due-braccio, o di tempo in sequenza codifica il bifase modelli in SLM (precedente introduzione di uno specchio di riferimento nell'impostazione di ottica). In entrambi i casi, non c'è nessuna necessità di filtro spaziale e di conseguenza senza perdita di risoluzione spaziale, a scapito di aumentare la complessità del sistema ottico, come pure il processo di allineamento. Qui, va anche sottolineato che utilizzando questo metodo di codifica, l'intero spettro del campo complesso desiderato può essere Estratto esattamente sul piano della trasformata di Fourier, dopo il filtraggio di tutti gli ordini di diffrazione, ma il numero zero uno.
D'altra parte, l'efficienza del metodo dipende da diversi fattori: le specifiche del produttore di SLM (ad es., fill factor, riflettività o diffrazione efficienza), la dimensione del pattern codificato e il modo in cui la luce incide sulla SLM (riflessione con un piccolo angolo di colpire, o incidenza normale utilizzando un divisore di fascio). A questo punto, in condizioni sperimentali adeguate, l'efficienza luminosa totale misurata può essere superiore al 30%. Tuttavia, si noti che che l'efficienza luminosa totale solo grazie all'uso di SLM può essere inferiore al 50%. La mancanza di casuale o elementi di diffusore interno ottica installazione permette il recupero dei modelli di ampiezza e fase senza rumore coerente (macchiolina). Altri aspetti significativi da sottolineare sono l'utilizzo di un algoritmo di codificazione diretto piuttosto che procedure iterative e la sua capacità di eseguire arbitraria ed indipendente di ampiezza e modulazione di fase alla frequenza di aggiornamento tempo di SLM (fino a centinaia di hertz secondo la tecnologia attuale).
In linea di principio, il metodo7 è destinato a essere utilizzato con onde piane input, ma non è limitato a quello. Per esempio, se un fascio gaussiano sta colpendo la SLM, è possibile modificare la forma di irraggiamento l'output del sistema dalla codifica di un modello adatto di ampiezza in SLM. Tuttavia, come l'intensità del fascio di uscita non può superare quello del fascio luminoso ingresso in qualsiasi posizione trasversale (x, y), la modellatura dell'ampiezza viene eseguita dalle perdite di intensità originate da un processo di interferenza distruttiva parzialmente.
La teoria sottolineando la codifica di metodo7 è come segue. Qualsiasi campo complesso rappresentato in forma U(x,y)= A(x,y)eφ(x,y) può anche essere riscritta come:
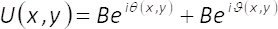 (1)
(1)
dove
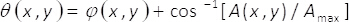 (2)
(2)
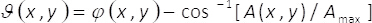 (3)
(3)
Nelle equazioni 1-3, l'ampiezza e la fase del complesso bidimensionale campo U(x,y)è dato da A(x,y) e φ(x,y), rispettivamente. Si noti che, in termini di unmax (massimo di A(x,y)) e B = unmax/2 non dipendono le coordinate trasversale (x,y). Dalla teoria, se abbiamo impostato unmax= 2, allora B =1. Quindi, il campo complesso U(x,y) può essere ottenuta, in modo semplice, dalla somma coerente di uniforme onde essereioϑ(x,y) e essere iΘ (x,y). In pratica, questa operazione viene eseguita con un interferometro di comune-percorso costituito da una singola fase elemento α(x,y), posizionato sul piano di ingresso di un sistema di imaging. L'elemento di monofase è costruito di multiplexing spaziale dei termini di fase ϑ(x,y)
e θ (x,y) con l'aiuto di grigliati binari bidimensionale (scacchiera) M1(x,y) e M.2(x,y) come segue
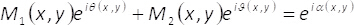 (4)
(4)
da qui,
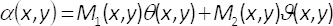 (5)
(5)
Questi modelli binari soddisfano la condizione M1(x,y) + M2(x,y) = 1. Si noti che, l'interferenza delle onde uniforme non può avvenire se non mescoliamo le informazioni contenute nel elemento di faseα(x,y). Il presente metodo, questo avviene utilizzando un filtro spaziale in grado di bloccare tutti gli ordini di diffrazione, ma il numero zero uno. In questo modo, dopo il processo di filtraggio sul piano della trasformata di Fourier, lo spettro H(u,v)= F{eiα(x,y)} della fase codificata funzione è legata allo spettro del campo complesso F{U(x,y)} dall'espressione
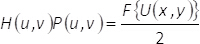 (6)
(6)
Nella sezione EQ. (6), (u,v) denotare coordinate nel dominio della frequenza, P(u,v) vale per il filtro spaziale, mentre la trasformata di Fourier di una funzione specificata Θ(x,y) è rappresentato in forma F {Θ(x,y)}. Da EQ. (6), ne consegue che, sul piano di uscita del sistema di imaging, il campo complesso Estratto URET(x,y), (senza considerare fattori costanti), è dato dalla convoluzione dell'ingrandita e spazialmente invertito campo complesso U(x,y) con la trasformata di Fourier della maschera di filtro. Cioè:
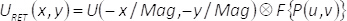 (7)
(7)
In EQ. (7), l'operazione di convoluzione è denotato dal simbolo  e il termine Mag rappresenta l'ingrandimento del sistema di imaging. Quindi, l'ampiezza e la fase di U(x,y) è completamente Estratto piano di uscita, ad eccezione di qualche perdita di risoluzione spaziale a causa dell'operazione di convoluzione.
e il termine Mag rappresenta l'ingrandimento del sistema di imaging. Quindi, l'ampiezza e la fase di U(x,y) è completamente Estratto piano di uscita, ad eccezione di qualche perdita di risoluzione spaziale a causa dell'operazione di convoluzione.
Access restricted. Please log in or start a trial to view this content.
Protocollo
1. codifica il campo complesso in un elemento di monofase
- Le specifiche tecniche di SLM, trovare la risoluzione spaziale (per esempio 1920 pixel x 1800 pixel).
- Definire e generare l'ampiezza desiderata A(x,y) e la fase φ(x,y) modelli come immagini digitali.
- Impostare la risoluzione spaziale delle suddette immagini digitali pari a quella del display SLM.
- Set di immagini digitali di cui sopra in formato livello grigio.
- Impostare i valori minimi e massimi delle immagini di fase e di ampiezza da 0 a 255 e da - π/2 e π/2, rispettivamente.
- Impostare unmax = 2 nelle equazioni 2 e 3 e computer-generare la fase modelli ϑ(x,y) e θ(x,y) da loro.
- Computer generare la scacchiera M1(x,y) e M.2(x,y).
- Impostare la risoluzione spaziale di questi modelli della scacchiera pari a quella del display SLM.
- Per ridurre l'effetto di diafonia pixel, generare altre coppie di scacchiera M1(x,y) e M.2(x,y) costruiti con celle di pixel differenti con un aumentato il numero di pixel (per esempio: cellule di pixel 2x2, 3x3 e 4x4, ecc.).
Attenzione: Quando si aumenta la cella di pixel, il numero totale di pixel scacchiera deve rimanere invariato e pari alla risoluzione spaziale di SLM. Garantire che il numero finale dei pixel scacchiera tutti i rimane lo stesso dopo aver modificato le loro cellule di pixel.
- Computer di generare l' elemento di singola fase α(x,y) dall'equazione 5.
Nota: Vedere materiale supplementare denominato "MATLAB_code_1.m" per le attività correlate al passo 1 del presente protocollo.
2. ricostruzione del campo complesso
- Utilizzare un fascio laser collimato, lineare polarizzata e spazialmente coerente come una fonte di luce.
- Utilizzare una sola fase SLM con almeno 2 π gamma monofase.
- Quando necessario, è possibile utilizzare un espansore del fascio corretto per regolare le dimensioni del fascio per la dimensione del display SLM.
- Quando necessario, è possibile utilizzare un polarizzatore ottico per impostare polarizzazione fascio laser nella direzione orizzontale. Questo è solitamente importante per il corretto funzionamento di SLM sola fase, che sono in genere progettati per modulare la fase spaziale del campo elettromagnetico che oscillano nella direzione orizzontale, mantenendo inalterate le componenti verticali.
- Per poter inviare uno schema di fase per la SLM, seguire i protocolli di comunicazione standard indicati dal costruttore di SLM per collegare e controllare la SLM con il computer.
Nota: Protocollo comune per questo scopo include l'uso di una curva di calibrazione per trasformare i valori in radianti (a causa di operazioni matematiche con angoli) in livello di grigio quelle, che l'unità di controllo elettronico di SLM finalmente convertirà in livelli di tensione. Inoltre, come la SLM è collegato al computer come un dispositivo esterno con il proprio schermo, un'estensione dello schermo del computer è solitamente necessaria, come pure un programma adeguato per trasmettere le immagini di livello grigie corrispondente a questa schermata supplementare. Un esempio di questi codici è anche incluso come materiale supplementare (si veda MATLAB_code_2.m). - Implementare un sistema ottico di immagine e mettere il display di SLM nel piano ingresso di questo sistema.
- Utilizzare una lente di rifrazione di una lunghezza focale f per costruire un sistema di immagine otticaf 2f x 2 (un sistema ottico 4f è anche valido per questa attività). In conformità con il formato di output previsto del campo complesso, larghezza, lunghezza d'onda della luce e dello spazio fisico disponibile, impiegare lente/lenti con specifiche tecniche adatte (ad es., rivestimento, dimensioni, lunghezza focale, ecc.).
- Per trovare la posizione del piano di uscita del sistema di imaging, inviare il modello di fase α(x,y) per la SLM e cercare visivamente l'immagine registrata (a seconda della posizione della telecamera) con la migliore risoluzione spaziale.
Attenzione: In caso di basso-dimensioni pixel cellule (per esempio, 1x1 pixel) ed esposizioni SLM con larghezze di pixel di pochi micron (per esempio, 8 µm), solo il fascio propagazione può produrre interferenza tra onde uniforme codificate, ottenendo un immagini ricostruite senza includere l'iride circolare nel sistema di imaging. Utilizzare celle basso-dimensioni pixel per individuare la posizione del piano di uscita. - Posizionare un iride circolare di diametro variabile con l'aereo di Fourier del sistema ottico e allineare relativo centro con quello del fuoco del fascio laser.
- Per regolare le dimensioni dell'iride circolare sul piano della trasformata di Fourier, inviare il modello di fase α(x,y) e cercare visivamente l'immagine registrata (a seconda del diametro del diaframma circolare) con migliore risoluzione spaziale.
Attenzione: In caso di lungo-dimensione pixel cellule (per esempio, 4 x 4 pixel), l'interferenza tra onde uniforme codificate viene effettuata fondamentalmente con il filtro spaziale. Utilizzare cella lunga-dimensione pixel per regolare le dimensioni dell'iride circolare. In questo protocollo, i termini bassa e lunga-dimensioni si riferisce il numero di pixel contenuti in una cella di pixel. Tuttavia, l'interferenza di cui sopra dipende anche la larghezza in pixel. Impiegano slm con larghezze di pixel pari o inferiore a 8 µm.
- Invia l'immagine livello grigio corrispondente elemento fase α(x,y) per la SLM.
- Per ridurre al minimo l'effetto di diafonia, cercare le migliori dimensioni della cella pixel che permettono di ottenere l'immagine registrata con la maggiore risoluzione spaziale.
3. misurare il campo complesso ricostruito
- Implementare la base di polarizzazione di spostamento di fase tecnica8.
- Posizionare e allineare l'angolo di rotazione del primo polarizzatore ottico, situato appena prima il SLM (Vedi Figura 2). Per impostare l'angolo di rotazione del primo polarizzatore, cercare visivamente la trasmissione della luce massima e minima nella fotocamera CCD (posizionata sul piano di uscita del sistema di imaging), a seconda della rotazione del polarizzatore. Annotare i due angoli corrispondenti del polarizzatore. Fissare l'angolo finale del polarizzatore a quello tra i due angoli precedente registrato.
- Posizionare e allineare l'angolo di rotazione del secondo polarizzatore ottico, situato dopo il piano di Fourier del sistema di imaging (vedere la Figura 2). Per impostare l'angolo di rotazione del secondo polarizzatore, cercare visivamente le immagini più nitide e più sfocate nella fotocamera CCD (posizionato sul piano di uscita del sistema di imaging) dopo l'invio il reticolo di fase α(x,y) per la SLM. Annotare i due angoli corrispondenti del polarizzatore. Fissare l'angolo finale del secondo polarizzatore a quella tra gli angoli precedente registrato.
- Registrare l'interferogrammi.
- Tenere la telecamera CCD al piano di uscita del sistema di imaging.
- Per registrare il primo interferogramma, aggiungere una matrice di 0 radianti per l' elemento di fase α(x,y) e inviarlo a SLM. Registrare immagini corrispondenti ho1(x,y) con il CCD.
- Per registrare il secondo interferogramma, aggiungere una matrice di π/2 radianti per l' elemento di fase α(x,y) e inviarlo a SLM. Registrare immagini corrispondenti ho2(x,y) con la telecamera CCD.
- Per registrare il terzo interferogramma, aggiungere una matrice di π radianti per l' elemento di fase α(x,y) e inviarlo a SLM. Registrare immagini corrispondenti ho3(x,y) con la telecamera CCD.
- Per registrare il quarto e ultimo interferogramma, aggiungere una matrice di 3 π/2 radianti per l' elemento di fase α(x,y) e inviarlo a SLM. Registrare immagini corrispondenti ho4(x,y) con la telecamera CCD.
- Ricostruire il campo complesso.
Nota: Vedere materiale supplementare denominato "MATLAB_code_3.m" per le attività correlate su questo punto del protocollo.- Recuperare l'ampiezza del campo complesso unEstratto(x,y) utilizzando l'espressione
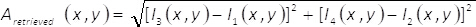 (8)
(8) - Recuperare la fase del campo complesso φEstratto(x,y) utilizzando l'espressione
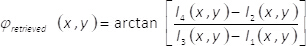 (9)
(9)
- Recuperare l'ampiezza del campo complesso unEstratto(x,y) utilizzando l'espressione
Access restricted. Please log in or start a trial to view this content.
Risultati
La risoluzione spaziale di SLM sola fase autonomo è 1920 pixel x 1080 pixel, con un pixel pitch di 8 µm. L'ampiezza selezionati A(x,y) e la fase φ(x,y) del campo complesso sono definiti da due diverse immagini di livello grigi corrispondente alla foto di Lenna ben noto (modello di ampiezza) e una giovane ragazza conficca fuori la lingua (modello di fase), rispettivamente. In generale, per entrambi, la generazione di modelli necessar...
Access restricted. Please log in or start a trial to view this content.
Discussione
In questo protocollo, parametri pratici come la larghezza in pixel di sola fase SLM o il numero di pixel contenuti all'interno delle cellule di pixel di un modello generato da calcolatore sono punti chiave per implementare con successo il metodo di codifica. In pochi passi 1.2, 1.3 e 1.4 del protocollo, più è breve la larghezza in pixel, migliore è la risoluzione spaziale dei modelli Estratto di ampiezza e fase. Inoltre, come la codificazione in SLM di brusche modulazioni di fase di pixel per pixel può originare risp...
Access restricted. Please log in or start a trial to view this content.
Divulgazioni
Gli autori non hanno nulla a rivelare.
Riconoscimenti
Questa ricerca è stata sostenuta dalla Generalitat Valenciana (PROMETEO 2016-079), Universitat Jaume I (UJI) (UJIB2016-19); e Ministerio de Economía y Competitividad (MINECO) (FIS2016-75618-R). Gli autori sono molto grati per la SCIC di Universitat Jaume I per l'utilizzo del laser a femtosecondi.
Access restricted. Please log in or start a trial to view this content.
Materiali
| Name | Company | Catalog Number | Comments |
| Achromatic Doublet | THORLABS | AC254-100-B-ML | Lens Diameter 25.4 mm, focal length 100 mm |
| Achromatic Galilean Beam Expander | THORLABS | GBE05-A | AR Coated: 400 - 650 nm |
| Basler camera | BASLER | avA1600-50gm GigE camera | sensor size 8.8 mm x 6.6 mm, pizel size 5.5 microns |
| Mounted Zero-Aperture Iris | THORLABS | ID12Z/M | Max Aperture 12 mm |
| Pellicle Beamsplitter | THORLABS | CM1-BP145B2 | 45:55 (R:T), Coating: 700 - 900 nm |
| PLUTO Spatial Light Modulator | HOLOEYE Photonics AG | NIR-II | Phase Only Spatial Light Modulator (Optimized for 700 -1000 nm) |
| Two thin film laser polarizers | EKSMA OPTICS | 420-0526M | material BK7, diameter 50 mm, wavelength 780-820 nm |
Riferimenti
- Hsueh, C. K., Sawchuk, A. A. Computer-generated double-phase holograms. Applied Optics. 17 (24), 3874-3883 (1978).
- Arrizón, V. Complex modulation with a twisted-nematic liquid-crystal spatial light modulator: double-pixel approach. Optics Letters. 28 (15), 1359-1361 (2003).
- Arrizón, V., Ruiz, U., Carrada, R., González, L. A. Pixelated phase computer holograms for the accurate encoding of scalar complex fields. Journal of the Optical Society of America A. 24 (11), (2007).
- Shibukawa, A., Okamoto, A., Takabayashi, M., Tomita, A. Spatial cross modulation method using a random diffuser and phase-only spatial light modulator for constructing arbitrary complex fields. Optics Express. 22 (4), 3968-3982 (2014).
- Martínez-Fuentes, J. L., Moreno, I. Random technique to encode complex valued holograms with on axis reconstruction onto phase-only displays. Optics Express. 26 (5), 5875-5893 (2018).
- Clark, T. W., Offer, R. F., Franke-Arnold, S., Arnold, A. S., Radwell, N. Comparison of beam generation techniques using a phase only spatial light modulator. Optics Express. 24 (6), 6249-6264 (2016).
- Mendoza-Yero, O., Mínguez-Vega, G., Lancis, J. Encoding complex fields by using a phase-only optical element. Optics Letters. 39 (7), 1740-1743 (2014).
- Yamaguchi, I., Zhang, T. Phase-shifting digital holography. Optics Letters. 22 (16), 1268-1270 (1997).
- Shao, Y., et al. Addressable multiregional and multifocal multiphoton microscopy based on a spatial light modulator. Journal of Biomedical Optics. 17 (3), 030505(2012).
- Mendoza-Yero, O., Carbonell-Leal, M., Mínguez-Vega, G., Lancis, J. Generation of multifocal irradiance patterns by using complex Fresnel holograms. Optics Letters. 43 (5), 1167-1170 (2018).
- Kuang, Z., et al. Diffractive Multi-beam Ultra-fast Laser Micro-processing Using a Spatial Light Modulator (Invited Paper). Chinese Journal of Lasers. 36 (12), 3093-3115 (2009).
- Kuang, Z., et al. High throughput diffractive multi-beam femtosecond laser processing using a spatial light modulator. Applied Surface Science. 255, 2284-2289 (2008).
Access restricted. Please log in or start a trial to view this content.
Ristampe e Autorizzazioni
Richiedi autorizzazione per utilizzare il testo o le figure di questo articolo JoVE
Richiedi AutorizzazioneThis article has been published
Video Coming Soon