Induzione del microstreaming mediante oscillazioni di bolle non sferiche in un sistema di levitazione acustica

Riepilogo

Viene proposta una tecnica veloce e affidabile per controllare le oscillazioni di forma di una singola bolla acustica intrappolata che si basa sulla tecnica della coalescenza tra due bolle. Le oscillazioni della forma della bolla controllate da simmetria e allo stato stazionario consentono l'analisi del flusso di fluido generato in prossimità dell'interfaccia della bolla.

Abstract

Quando si trovano vicino a barriere biologiche, le microbolle oscillanti possono aumentare la permeabilità della membrana cellulare, consentendo l'internalizzazione di farmaci e geni. Osservazioni sperimentali suggeriscono che la permeabilizzazione temporanea di queste barriere può essere dovuta allo stress di taglio che viene esercitato sui tessuti cellulari dal microstreaming di cavitazione. Il microstreaming a cavitazione è la generazione di flussi di vortice che sorgono attorno a microbolle ad ultrasuoni oscillanti. Per produrre tali flussi di liquido, le oscillazioni delle bolle devono deviare dalle oscillazioni puramente sferiche e includere un'instabilità traslazionale o modi di forma. Gli studi sperimentali sui flussi indotti dalle bolle e sullo sforzo di taglio sulle superfici vicine sono spesso limitati nella loro portata a causa della difficoltà di catturare le deformazioni di forma delle microbolle in modo stabile e controllabile. Descriviamo il progetto di una camera a levitazione acustica per lo studio delle oscillazioni non sferiche controllate dalla simmetria. Tale controllo viene eseguito utilizzando una tecnica di coalescenza tra due bolle in avvicinamento in un campo ultrasonico sufficientemente intenso. Il controllo delle oscillazioni non sferiche apre la strada a un microstreaming a cavitazione controllata di una microbolla oscillante a superficie libera. Le telecamere ad alto frame rate consentono di indagare quasi simultaneamente la dinamica delle bolle non sferiche alla scala temporale acustica e il flusso del liquido su una scala temporale inferiore. È dimostrato che è possibile ottenere una grande varietà di modelli fluidi e che sono correlati al contenuto modale dell'interfaccia a bolle. Dimostriamo che anche le modalità di forma di ordine elevato possono creare modelli fluidi a grande distanza se la dinamica dell'interfaccia contiene diverse modalità, evidenziando il potenziale delle oscillazioni non sferiche per la somministrazione mirata e localizzata del farmaco.

Introduzione

In medicina, un farmaco somministrato deve penetrare molti ostacoli nel sistema vivente prima di raggiungere gli obiettivi desiderati. Tuttavia, la maggior parte dei farmaci vengono rapidamente puliti dal flusso sanguigno. L'efficienza del targeting è bassa e non possono facilmente attraversare le membrane cellulari, portando a una somministrazione inefficace del farmaco. Attualmente, l'uso di microbolle in combinazione con gli ultrasuoni è stato proposto come metodo innovativo per la somministrazione non invasiva, precisa e mirata di farmaci e geni a tessuti e cellule patologici¹. In questo approccio, le microbolle possono svolgere un ruolo come vettori in cui i farmaci liberi vengono co-iniettati con una sospensione di bolle di gas o caricati sulla sua superficie. Le microbolle possono anche fungere da vettore locale per rifocalizzare l'energia degli ultrasuoni al fine di interagire con le cellule. Fondamentalmente, sotto l'esposizione agli ultrasuoni, le bolle si comprimono e si espandono in modo stabile, un regime chiamato cavitazione stabile che genera flussi di liquido e quindi stress da taglio sugli oggetti vicini. Le microbolle possono anche oscillare in modo non lineare ed espandersi fino al collasso, nel regime di cavitazione inerziale, producendo onde d'urto che si propagano radialmente dal sito di collasso². È stato dimostrato che la cavitazione, stabile o inerziale, aumenta la permeabilizzazione delle membrane cellulari e quindi migliora l'internalizzazione dei farmaci nella cellula³.

Nelle applicazioni terapeutiche, comprendere il meccanismo dell'interazione bolla-cellula è molto importante, ma ci sono diverse barriere, sia dal lato scientifico che tecnico, che impediscono alla nostra conoscenza di avanzare. In primo luogo, catturare la dinamica delle cellule in risposta a stimoli meccanici indotti da bolle è molto difficile⁴. Alla scala temporale acustica, le oscillazioni delle microbolle del primo ordine possono portare all'attivazione dei canali di membrana, facilitando il passaggio molecolare attraverso le interfacce biologiche. Ciò avviene attraverso l'oscillazione diretta della membrana cellulare, chiamata anche "massaggio cellulare"⁵. L'attivazione del canale a seguito di stress meccanico diretto è stata evidenziata utilizzando tecniche patch-clamp che hanno misurato le proprietà elettrofisiologiche delle membrane cellulari durante e dopo l'esposizione agli ultrasuoni⁶. Misurare la dinamica cellulare indotta da bolle (cioè il campo completo di deformazione della membrana cellulare) alla scala temporale acustica, fornirebbe anche informazioni sulla soglia di espansione dell'area della membrana Δ A/ A necessaria per indurre i pori nella membrana cellulare⁷. La seconda barriera è il controllo del regime di collasso delle bolle per evitare la lisi cellulare indotta da microbolle. I collassi delle bolle e i microgetti indotti sono stati identificati come un meccanismo attraverso il quale avviene la perforazione della membrana ^8,9. Una volta permeabilizzata, la membrana cellulare si ripara attraverso l'autosigillatura del calcio dei doppi strati lipidici e la fusione delle vescicole intracellulari⁹. Il verificarsi di collassi di bolle può anche causare danni letali alla cellula e indurre effetti collaterali non necessari in quelli circostanti. In applicazioni sensibili come l'apertura della barriera emato-encefalica mediata da ultrasuoni, è generalmente accettato che i collassi delle bolle inerziali dovrebbero essere evitati¹⁰.

Pertanto, enormi sforzi sono attualmente dedicati alla progettazione di sequenze di emissione di ultrasuoni, accoppiati con il monitoraggio e il controllo della cavitazione passiva, al fine di garantire oscillazioni stabili delle microbolle¹¹. In questo regime stabile, è stato ipotizzato che le bolle stabilmente oscillanti svolgano un ruolo importante nell'innesco della permeabilizzazione della membrana promuovendo lo stress di taglio spazialmente mirato sulla membrana cellulare⁷. Lo sforzo di taglio deriva dai flussi di liquido creati in prossimità delle bolle oscillanti. Questi flussi liquidi sono chiamati microstreaming di cavitazione e, come accennato in precedenza, sono uno dei diversi possibili meccanismi responsabili di un maggiore assorbimento di molecole extracellulari. Quando si tratta di sospensione di bolle o cellule come i saggi di trasfezione biologica in vitro¹², la permeabilizzazione mediante microstreaming potrebbe essere molto più efficiente della permeabilizzazione mediante collasso di bolle. Questo può essere dimostrato da una semplice considerazione geometrica. Nelle sospensioni cellulari, la sonoporazione sarà efficiente se la maggior parte delle cellule sospese è sottoposta ad effetti meccanici sufficientemente grandi (che portano alla permeabilizzazione della membrana). È noto che i collassi delle bolle sono diretti lungo la direzione di rottura della simmetria isotropa, come l'asse bolla-parete¹³ o la bolla-bolla e la linea bolla-cella che uniscono il loro centro di massa¹⁴. Il microgetto prodotto è quindi un fenomeno spazialmente localizzato lungo un numero finito di linee che uniscono i centri della cellula e della bolla. A seconda della concentrazione di cellule e bolle, nonché della distanza tra cellule a bolla, questo effetto potrebbe non essere il più efficiente per permeabilizzare l'intero numero di cellule sospese. Al contrario, il microstreaming di cavitazione è un fenomeno che si verifica su una scala temporale lenta, con una grande espansione spaziale rispetto al raggio della bolla. Inoltre, il flusso di liquido è distribuito intorno alla bolla e può quindi avere un impatto su un numero maggiore di cellule, a un raggio molto lungo. Pertanto, comprendere il microstreaming di cavitazione generato attorno a una bolla oscillante è un prerequisito per controllare e quantificare lo stress di taglio indotto dalla bolla che viene applicato alle cellule.

Per fare ciò, un passo preliminare consiste nel controllare le oscillazioni sferiche e non sferiche di una bolla guidata da ultrasuoni, poiché i flussi di liquido generati sono indotti dal moto dell'interfaccia della bolla^15,16. In particolare, le oscillazioni di forma delle microbolle devono essere innescate e mantenute stabili. Inoltre, l'orientamento delle oscillazioni della forma della bolla deve essere controllato per analizzare correttamente la correlazione tra la dinamica dell'interfaccia della bolla e il modello di microstreaming indotto. Quando si riassume la letteratura esistente, è ovvio che i risultati sperimentali dettagliati del microstreaming indotto dalla cavitazione sono disponibili solo per le bolle attaccate a una superficie. Le microbolle attaccate a parete sono comunemente utilizzate per valutare accurate dinamiche di interfaccia e interazioni cellulari su scala micrometrica sotto un sistema di microscopia ultraveloce. Questa configurazione è terapeuticamente rilevante quando si considerano microbolle vibranti situate sulla membrana cellulare^17,18,19. Lo studio della bolla attaccata al substrato può tuttavia rendere più complicata l'analisi della dinamica delle bolle, in parte a causa della natura complessa della dinamica della linea di contatto²⁰ e dell'attivazione dei modi di forma asimmetrica²¹. Nelle applicazioni mediche e biologiche, le bolle che non sono attaccate a una parete si trovano comunemente in geometrie confinate come piccoli vasi. Ciò influisce in modo significativo sulla dinamica delle bolle e sulle instabilità della forma. In particolare, la presenza di una parete vicina sposta la soglia di pressione per la modalità forma innescando valori di pressione più bassi a seconda del numero della modalità forma e della dimensione della bolla²². La parete influisce anche sul microstreaming indotto dalla bolla con intensità possibilmente maggiore per il flusso prodotto²³.

Tra tutti i possibili scenari che le microbolle possono sperimentare (libere o attaccate, vicine a una parete, collassate o stabilmente oscillanti), ci proponiamo di indagare la dinamica non sferica di una singola bolla lontana da ogni confine. La configurazione sperimentale si basa su un sistema di levitazione acustica²⁴ in cui viene utilizzata un'onda ultrasonica stazionaria per intrappolare la bolla. Questo scenario è coerente con le applicazioni mediche in cui una raccolta di bolle e cellule sospese coesistono in una camera di sonotransfezione, per esempio. Nella misura in cui le bolle e le celle non sono troppo vicine, si presume che la presenza di una cella non influisca sulla dinamica dell'interfaccia delle bolle. Quando le cellule seguono le traiettorie ad anello del microstreaming indotto dalla cavitazione, si avvicinano ciclicamente e respingono dalla posizione della bolla e possiamo supporre che la presenza cellulare non influisca né sul modello di flusso né sulla sua velocità media. Inoltre, la dinamica non sferica e il microstreaming indotto da singole bolle lontane dal confine sono ben noti da un punto di vista teorico. Per collegare il flusso di liquido indotto dalla bolla alla dinamica del contorno della bolla, è necessario caratterizzare accuratamente la dinamica dell'interfaccia della bolla. Per fare ciò, è preferibile adattare la scala spazio-temporale negli studi sperimentali rispetto a quelli utilizzati nelle terapie in modo che l'acquisizione con le comuni telecamere ad alta velocità (inferiori a 1 milione di fotogrammi / secondo) sia possibile utilizzando grandi bolle eccitate a frequenze più basse. Quando si considerano bolle non rivestite, l'autofrequenza ω n di un dato modo _n è correlata alla dimensione della bolla come 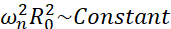²⁵. Questa relazione raggio-autofrequenza è leggermente modificata quando si considerano le bolle sgusciate²⁶, ma l'ordine di grandezza dell'autofrequenza ω_n rimane lo stesso. Pertanto, studiare bolle con raggi di equilibrio ~ 50 μm in un campo di ultrasuoni a 30 kHz è simile allo studio di bolle rivestite di raggi ~ 3 μm in un campo di 1,7 MHz, come proposto da Dollet et ^al.27. Sono quindi previsti numeri di modalità di forma simili e quindi modelli di microstreaming.

Per innescare oscillazioni non sferiche dell'interfaccia a bolla, è necessario superare una certa soglia di pressione dipendente dal raggio, come mostrato in Figura 1. Le tecniche sperimentali esistenti si basano sull'aumento della pressione acustica per innescare i modi superficiali (illustrati dal percorso (1) nella figura 1), sia mediante aumento graduale della pressione²⁸ o mediante eccitazione ad ampiezza modulata responsabile dell'insorgenza periodica e dell'estinzione dei modi superficiali²⁹. I principali svantaggi di queste tecniche sono (i) un orientamento casuale dell'asse di simmetria delle oscillazioni superficiali che non possono essere controllate per essere nel piano di imaging, (ii) una breve durata delle oscillazioni della forma della bolla che rende difficile l'analisi dei flussi di liquido indotti su scale temporali più ampie e (iii) il frequente innesco di modalità di forma instabili. Proponiamo una tecnica alternativa per attraversare la soglia di pressione ad una pressione acustica costante nella mappa raggio/pressione, come illustrato dal percorso (2) nella Figura 1. Per fare ciò, è necessario aumentare la dimensione della bolla in modo tale che si trovi nella zona di instabilità. Tale aumento viene eseguito con una tecnica di coalescenza a bolle. La coalescenza di due microbolle, inizialmente sfericamente oscillanti, viene sfruttata per creare una singola bolla deformata. Se la pressione acustica e la dimensione della bolla della bolla a coalescenza si trovano nella zona di instabilità, vengono attivate le modalità di superficie. Abbiamo anche evidenziato che la tecnica della coalescenza induce oscillazioni di forma stabili in un regime di stato stazionario, nonché un asse di simmetria controllato definito dal movimento rettilineo delle due bolle in avvicinamento. Poiché un'oscillazione della forma stabile è garantita per pochi minuti, l'analisi del flusso di fluido indotto dalla bolla è possibile seminando il mezzo liquido con microparticelle fluorescenti, illuminate da un sottile foglio laser. La registrazione del movimento delle microparticelle solide in prossimità dell'interfaccia della bolla consente di identificare il modello del flusso di fluido indotto³⁰. Il principio generale dell'innesco delle oscillazioni a forma di bolla, che portano a un flusso di fluido stabile nel tempo, è illustrato nella Figura 2.

Nel seguente protocollo, delineiamo i passaggi necessari per creare oscillazioni stabili della forma della bolla attraverso la tecnica della coalescenza e descriviamo le misurazioni del flusso del fluido. Ciò include la progettazione del sistema di levitazione acustica, la calibrazione acustica, la nucleazione delle bolle e la tecnica di coalescenza, la misurazione della dinamica dell'interfaccia delle bolle e del flusso del fluido circostante e l'elaborazione delle immagini.

Protocollo

1. Progettazione della camera a levitazione acustica

1. Progettare un serbatoio cubico otticamente trasparente (simile al PMMA) (bordo di 8 cm e spessore di 2,8 mm per faccia) con il modulo di geometria di un software di simulazione multifisica (Table of Materials).
2. Inserire una superficie cilindrica (Ø = 35 mm) centrata sul fondo del serbatoio, per modellare il trasduttore ad ultrasuoni.
3. Impostare le condizioni al contorno su zero pressione su ciascuna parete con uno spostamento normale di ampiezza 1 μm sulla superficie del trasduttore.
4. Utilizzando un modulo di dominio della frequenza, simulare la funzione di risposta in frequenza (FRF) del serbatoio nella gamma di frequenza [10 - 40] kHz, nelle tre posizioni arbitrarie loc1 = (0,01375, 0,01375, 0,04125), loc2 = (0, 0, 0,0088) e loc3 = (0,021725, 0,023375, 0,00935).
5. Adattare le dimensioni del serbatoio in modo tale che una delle modalità acustiche della cavità corrisponda alla frequenza nominale del trasduttore (qui 31,2 kHz). L'FRF contiene quindi un picco di risonanza vicino a questa frequenza, come illustrato nella Figura 3.
6. Tracciare il campo di pressione all'interno del serbatoio, come mostrato nella Figura 4. La modalità di risonanza scelta deve contenere almeno un antinodo di pressione all'interno del contenitore, sul quale verrà intrappolata la bolla acustica.
7. Quando si progetta il serbatoio, progettare una faccia superiore mobile con una scanalatura guida su ciascun bordo per chiudere saldamente le facce del serbatoio. Praticare un piccolo foro sulla faccia superiore per riempire il serbatoio con il mezzo liquido.
8. Posizionare il serbatoio dell'acqua sopra un telaio fatto in casa che contiene il trasduttore a ultrasuoni (tipo Langevin, frequenza nominale 31,2 kHz). Utilizzare il gel ecografico per accoppiare il trasduttore alla parete inferiore del serbatoio.
9. Posizionare il serbatoio e il sistema di telaio su una tavola di spostamento a tre direzioni con viti micrometriche.
10. Riempire il serbatoio con acqua microfiltrata, demineralizzata e (non degassata, volume ~500mL, saturazione di ossigeno di circa 8 mg· ^L-1).
    NOTA: L'uso di acqua non degassata invece di quella degassata consente di mantenere bolle stabili per tutta la durata degli esperimenti. L'uso di acqua degassata accelererà il restringimento delle bolle a causa della diffusione del gas, anche se leggermente controbilanciato dalla diffusione rettificata (mediata dagli ultrasuoni).

2. Generazione di bolle e calibrazione acustica

1. Preparare la configurazione sperimentale utilizzata per la nucleazione di bolle indotta dal laser, l'eccitazione acustica e la registrazione ad alta velocità (Figura 5a, b, c). La configurazione sperimentale consiste in (A) il sistema di levitazione acustica, (B) l'alimentazione laser e (C) la testa laser, (D) una lente concava sferica, (E) una lente plano-concava e una lente asferica, (F) la telecamera ad alta velocità, (G) il diodo continuo a emissione di luce. Successivamente, per le misure dei flussi di liquidi (Figura 5d) (H) verrà aggiunta una sorgente laser ad onda continua, (I) una lente cilindrica plano-concava seguita da una lente cilindrica plano-concava inserita dietro la prima lente e orientata sull'asse ortogonale.
2. Collegare il trasduttore a ultrasuoni a un generatore di funzioni. Impostare il segnale di eccitazione come: forma d'onda sinusoidale, onda continua, frequenza 31,2 kHz. L'ampiezza è l'unico parametro variabile.
3. Posizionare la lente (D) a una distanza di circa 6 cm davanti alla testa laser (C).
4. Posizionare la lente (E) a una distanza di circa 12 cm davanti alla lente (D).
5. Posizionare il serbatoio dell'acqua (A) in modo tale che un punto di messa a fuoco del laser si trovi all'interno del serbatoio dell'acqua, portando alla generazione di scintille per ogni impulso laser (5 -10 mJ). La scintilla laser deve essere posizionata a circa 3 cm sotto l'antinodo di pressione mirato.
   NOTA: Senza ultrasuoni (US), la bolla nucleata con laser salirà verso la faccia superiore a causa della galleggiabilità.
6. Accendere il trasduttore ad ultrasuoni. Aumentare la tensione applicata fino a quando la bolla non si alza più verticalmente ma viene deviata verso l'antinodo di pressione e, per una pressione sufficientemente elevata, intrappolata.
7. Impostare l'illuminazione retroilluminata (diodo a emissione continua di luce) e la telecamera ad alta velocità per osservare la bolla intrappolata.
   NOTA: Quando si nuclanizza una nuova bolla con una scintilla laser, è facile catturare la traiettoria della bolla che si avvicina alla sua posizione di intrappolamento.
8. Spostare la posizione della scintilla laser all'interno del serbatoio dell'acqua in modo che la traiettoria della bolla rimanga all'interno del piano focale della fotocamera.
9. Intrappola una bolla e cattura le sue oscillazioni radiali con i seguenti parametri: dimensioni del fotogramma 128 x 128 pixel, velocità di acquisizione 180 kHz. Un esempio di oscillazioni radiali di grande ampiezza su due periodi acustici è fornito nella Figura 6. La dimensione tipica delle bolle di gas varia da 30 a 80 μm.
10. Registra le oscillazioni radiali delle bolle durante 3-30 millisecondi per catturare centinaia di migliaia di oscillazioni di bolle. Ripetere questa registrazione per aumentare le tensioni applicate del trasduttore. Le tensioni applicate tipiche sono comprese tra 0 e 8 V.
    NOTA: quando si modifica la tensione applicata, la posizione di equilibrio della bolla intrappolata si sposta leggermente verticalmente. Per seguire le oscillazioni senza spostare l'illuminazione retroilluminata e la telecamera, posizionare il sistema (trasduttore e serbatoio dell'acqua) su un tavolo mobile a tre direzioni con precisione micrometrica.
11. Accendere il trasduttore a ultrasuoni e acquisire un'immagine dello sfondo per la post-analisi.
12. Post-elaborare la serie di video seguendo questa procedura:
    1. Eseguire il file eseguibile VoltagePressure.exe. L'interfaccia mostrata nella Figura 7 dovrebbe aprirsi.
       Nota : lo script è disponibile come documento supplementare.
    2. Specificare i parametri fisici e sperimentali nella colonna di sinistra (Figura 7A).
    3. Specificare i valori della tensione applicata per la serie di registrazioni nella tabella in basso a destra (Figura 7B).
    4. Nel pannello Analisi raggio bolla , fare clic su Parametri di caricamento (Figura 7C) e selezionare la cartella contenente tutti i file della serie di video, quindi l'immagine di sfondo (obbligatorio).
    5. La scelta è consentita tra l'analisi di tutti i video contemporaneamente, facendo clic su Auto, o uno per uno facendo clic su Passo dopo passo.
    6. Per ogni file video, l'evoluzione del raggio della bolla viene tracciata su un periodo acustico e viene sovrapposto un adattamento numerico. La curva rossa corrisponde a una modellazione linearizzata di Rayleigh-Plesset. Viene visualizzato il raggio della bolla di equilibrio (Figura 7D).
    7. In base al raccordo numerico, la pressione applicata per questa tensione viene visualizzata nel pannello grafico Pressione (tensione) (Figura 7E). Il valore della pressione applicata è visualizzato anche nella tabella in basso a destra (Figura 7B). Le pressioni tipiche applicate corrispondenti alla dinamica della tensione 0 - 8 V sono 0 - 25 kPa.
    8. Una volta elaborati tutti i video, fai clic sul pulsante Regressione lineare per eseguire un adattamento lineare della curva pressione/tensione. I dati (valori di tensione e pressione) vengono salvati in un file .txt che si trova nella directory corrente. Viene fornita la pendenza dell'adattamento.

3. Tecnica della coalescenza

1. Accendere il trasduttore ad ultrasuoni. Impostare la tensione applicata sufficientemente alta in modo tale che la pressione acustica corrispondente possa portare all'innesco dell'instabilità superficiale, secondo il diagramma numerico pressione/raggio delle zone di instabilità, come mostrato in Figura 8.
2. Nucleare una bolla, che migrerà poi nella sua posizione di intrappolamento. Se la bolla intrappolata mostra solo oscillazioni sferiche, passare al passaggio successivo. Se compaiono oscillazioni non sferiche:
   1. Spegnere la potenza degli ultrasuoni per consentire alla bolla di salire sulla superficie superiore.
   2. Modificare l'energia del laser (sintonizzando finemente su alcuni mJ) o ridurre la tensione del trasduttore.
   3. Accendere la potenza degli ultrasuoni.
   4. Nucleare una nuova bolla.
   5. Ripeti questa procedura fino a quando la dimensione della bolla porta a oscillazioni puramente sferiche.
3. Quando una bolla intrappolata mostra solo oscillazioni sferiche, genera una nuova scintilla laser. Quando la nuova bolla raggiunge la posizione di intrappolamento, si verifica la coalescenza.
4. Se la bolla coalescente mostra solo oscillazioni sferiche, generare una nuova bolla. Possono essere necessarie coalescenze multiple per raggiungere il raggio della bolla in cui si verificano deformazioni non sferiche. Un esempio di coalescenza delle bolle che porta a oscillazioni non sferiche è mostrato nella Figura 9.
5. Una volta che la bolla coalescente mostra oscillazioni non sferiche, registrare le oscillazioni della bolla per una durata approssimativamente compresa tra 3 e 30 millisecondi.
6. Identificate il numero di modalità delle oscillazioni di forma facendo riferimento alla Figura 10.

4. Misurazioni del flusso del fluido

1. Nel caso di misurazioni microstreaming di cavitazione, particelle traccianti fluorescenti devono essere aggiunte all'acqua prima della nucleazione della bolla. In questo studio vengono utilizzate particelle da 0,71 μm (Tabella dei materiali). Sono sufficientemente piccoli per essere acusticamente trasparenti (non influenzati dalla forza della radiazione acustica) e per seguire accuratamente il flusso, nonché sufficientemente grandi per diffondere la luce laser. Utilizzare tre gocce per il volume del serbatoio dell'acqua, corrispondenti a circa 2,10⁴ particelle / mm³.
2. Prima di effettuare le misurazioni, impostare i seguenti parametri per acquisire sia la dinamica delle bolle (scala temporale rapida) che il flusso del fluido (scala temporale bassa):
   1. Creare un partizionamento del disco di registrazione della fotocamera.
   2. In alternativa, definire i parametri di registrazione come:
      1. Frequenza fotogrammi 180 kHz, dimensioni del fotogramma 128 x 128 pixel e tempo di esposizione 1 μs per una registrazione della dinamica dell'interfaccia a bolle
      2. Frequenza fotogrammi 600 Hz, dimensioni del fotogramma 1024 x 768 pixel e tempo di esposizione 1 ms per una registrazione del movimento dei traccianti di colorante.
3. Utilizzare un laser continuo.
4. Creare un foglio laser sottile lasciando successivamente passare il raggio laser attraverso la lente cilindrica plano-concava e la lente cilindrica plano-convessa orientata su un asse ortogonale. È possibile ottenere una larghezza del fascio di circa 160 μm.
5. Impostare il foglio laser in modo che corrisponda al piano di imaging:
   1. Impostare il laser su un dispositivo mobile in modo che il foglio laser possa essere spostato parallelamente al piano di imaging.
   2. Regolare la posizione in modo che le particelle illuminate siano visibili dalla telecamera.
   3. Nucleate e intrappolate una bolla.
   4. Regolare ulteriormente la posizione del foglio laser, in modo che un'ombra diventi visibile dietro la bolla. La bolla si trova ora all'interno del foglio laser, come mostrato nella Figura 11.
6. Indurre la coalescenza delle bolle fino a quando non è evidente una modalità di forma stabilmente oscillante.
7. Fai diverse registrazioni passando avanti e indietro tra la dinamica delle bolle e il microstreaming.
   NOTA: spegnere il laser continuo quando non è necessario. Il riscaldamento può creare flussi convettivi indesiderati. Inoltre, spegnere il diodo a emissione luminosa quando si eseguono le misurazioni del flusso di flusso.

5. Elaborazione delle immagini per visualizzare i modelli di microstreaming di cavitazione

1. Installare il software di visualizzazione ImageJ per l'elaborazione e l'analisi delle immagini in Java. Installa anche il plugin CINE File Reader per aprire i file della telecamera ad alta velocità.
2. Clicca su File | Importazione | CineFile e selezionare il video *.cine contenente la cattura del movimento delle particelle.
3. Seleziona Usa stack virtuale nella nuova finestra, il video è ora caricato.
4. Per osservare il movimento delle particelle senza visualizzare il modello di streaming, fare clic su Immagine | Regola | Luminosità/Contrasto | Auto. Lo sfondo scuro è ora sostituito da un'immagine ottimizzata automaticamente.
5. Per visualizzare il modello risultante, fare clic su Immagine | Pile | Z Project e scegliete l'opzione Intensità massima per la proiezione dell'immagine. Viene visualizzata un'immagine di output con pixel contenenti il valore massimo su tutte le immagini nello stack. Se necessario, regolare il contrasto dell'immagine come descritto al punto 5.4.
   NOTA: si ottiene un modello di flusso come quelli illustrati nella Figura 12b e nella Figura 12d.

Risultati

Una sequenza completa di coalescenza di bolle che porta a oscillazioni non sferiche stabili nel tempo, controllate dalla simmetria, è presentata nella Figura 9. La fase di avvicinamento di due bolle oscillanti sfericamente termina quando il sottile film liquido tra le due bolle si rompe. Vale la pena notare che, nell'ultima fase prima della coalescenza, le interfacce delle bolle si discostano dalla sfericità. Entrambe le bolle si allungano su una forma elli...

Discussione

La procedura presentata consiste nell'utilizzare la coalescenza delle bolle al fine di innescare oscillazioni di forma della bolla stazionarie e controllate dalla simmetria, consentendo lo studio del flusso di fluido a lungo termine indotto da queste oscillazioni. La sfida principale nella tecnica è il controllo delle oscillazioni non sferiche per una bolla intrappolata, lontano da qualsiasi confine.

La maggior parte delle tecniche esistenti proposte in letteratura si sono concentrate sulle b...

Materiali

Name	Company	Catalog Number	Comments
Aspherical lens	Thorlabs	AL4050	Lens of focus 40 mm
Continuous wave laser source	CNI	MLL6FN	DPSS laser of wavelength 532nm, energy 400 mW
Cylindrical plano-concave lens	Thorlabs	LJ1277L1-A	lens of focus -25?4mm
Cylindrical plano-concave lens	Thorlabs	LK1900L1	lens of focus 250 mm
Fluorescent particles	Duke Scientific	R700	Red polymer fluorescent microspheres
Function generator	Agilent	HP33120	Generator of function feeding the ultrasound transducer
High-speed camera	Vision Research	Phantom v12.0	High-speed recording up to 1 Mfps
Liquid medium	Carlo Erba	Water for analysis	Demineralized, undegassed water
Multiphysics software	Comsol	None	Softwate for simulating the acoustic field of the levitation chamber
Nd:Yag pulsed laser	New Wave Research	Solo III-15	5 ns pulse duration, λ=532 nm, 3.5 mm beam diameter, up to 50 mJ
Plano-concave lens	Thorlabs	N-BK7	lens of focus 125 mm
Spherical concave lens	Thorlabs	N-SF11	Bi-concave lens of focus -25mm
Ultrasound transducer	SinapTec	Custom-made	Nominal frequency 31kHz, active area 35mm diameter
Visualization software	NIH	ImageJ	Software for image processing and analysis in Java
XY Linear stage	Newport	M-406	Displacement stage with micrometric screw
Z-axis linear stage	Edmund Optics	62-299	Vertical displacement stage with micrometric screw