Dinamica delle strutture
Panoramica
Fonte: Roberto Leon, Dipartimento di Ingegneria Civile e Ambientale, Virginia Tech, Blacksburg, VA
È raro al giorno d'oggi che un anno intero passa senza un grande evento sismico che provoca il caos da qualche parte in tutto il mondo. In alcuni casi, come il terremoto di Banda Ache del 2005 in Indonesia, i danni hanno coinvolto vaste aree geografiche e vittime a sei cifre. In generale, il numero e l'intensità dei terremoti non sta aumentando, tuttavia, la vulnerabilità dell'ambiente costruito è in aumento. Con la crescente urbanizzazione non regolamentata intorno ad aree sismicamente attive, come la "cintura di fuoco" circum-pacifica, l'innalzamento del mare in un'area costiera a bassa posa e l'aumento delle concentrazioni di nodi critici per la produzione / distribuzione di energia e la rete digitale / di telecomunicazione in aree vulnerabili, è chiaro che la progettazione resistente ai terremoti è la chiave per la futura resilienza della comunità.
La progettazione di strutture per resistere ai danni del terremoto è progredita notevolmente negli ultimi 50 anni, principalmente attraverso il lavoro in Giappone dopo il terremoto di Niigata del 1964 e negli Stati Uniti dopo il terremoto della San Fernando Valley del 1971. Il lavoro è progredito lungo tre binari paralleli: (a) lavoro sperimentale volto a sviluppare tecniche di costruzione migliorate per ridurre al minimo i danni e le perdite di vite umane; b) studi analitici basati su modelli avanzati di materiali geometrici e non lineari; e c) sintesi dei risultati di cui alle lettere a) e b) in disposizioni del codice di progettazione che migliorano la capacità delle strutture di resistere a carichi imprevisti.
I test sismici in laboratorio sono spesso difficili e costosi. I test vengono eseguiti principalmente utilizzando le seguenti tre tecniche:
- Test quasi-statico (QST), in cui parti di una struttura vengono testate utilizzando deformazioni laterali applicate lentamente e predeterminate in modo equivalente con condizioni al contorno idealizzate. Questa tecnica è particolarmente utile per valutare gli effetti dei dettagli strutturali sulla tenacità e la capacità di deformazione di particolari parti delle strutture.
- Test pseudo-dinamici (PSDT), in cui anche i carichi vengono applicati lentamente, ma gli effetti dinamici vengono presi in considerazione risolvendo le equazioni del moto man mano che il test progredisce e utilizzando feedback di test diretti (principalmente la rigidità istantanea) per valutare l'effettiva rigidità e le caratteristiche di smorzamento della struttura.
- Tavole discuotimento, in cui i modelli in scala di strutture complete sono soggetti a movimenti di input utilizzando una base o una fondazione azionata idraulicamente. Le tavole shake rappresentano una tecnica di prova più fedele, in quanto la struttura non è trattenuta artificialmente, l'input è vero movimento del terreno e le forze risultanti sono veramente inerziali, come ci si aspetterebbe in un terremoto reale. Tuttavia, i requisiti di alimentazione sono enormi e solo pochi tavoli shake in grado di funzionare quasi su larga scala esistono in tutto il mondo. A livello globale, c'è solo un grande tavolo di scuotimento in grado di eseguire test su strutture su larga scala, che è il tavolo di scuotimento presso la struttura E-Defense in Giappone, costruita all'indomani del terremoto di Kobe del 1985.
In questo esperimento, utilizzeremo un piccolo tavolo di scuotimento e strutture modello per studiare le caratteristiche di comportamento dinamico di alcuni modelli strutturali. Sono queste caratteristiche dinamiche, principalmente la frequenza naturale e lo smorzamento, nonché la qualità dei dettagli strutturali e della costruzione, che rendono le strutture più o meno vulnerabili ai terremoti.
Principi
C'è una differenza fondamentale tra i soliti carichi gravitazionali (auto-peso) che agiscono su una struttura, che sono quasi statici (cioè cambiano molto lentamente, o per niente con il tempo), e quelli prodotti da uragani, esplosioni e terremoti, che sono di natura estremamente dinamica. Nel caso di uragani e altri carichi di vento, è possibile modellare i loro effetti come pressioni statiche equivalenti in laboratorio in quanto la frequenza dei venti è molto lunga rispetto alla frequenza naturale fondamentale della struttura tipica. Importanti eccezioni a questo includono strutture flessibili, come ponti sospesi e sospesi a lunga campata, alberi alti e strutture di turbine eoliche, dove la frequenza naturale della struttura può corrispondere a quella delle raffiche di vento o dei venti dritti. Nel caso di terremoti, i carichi sono principalmente inerziali mentre il terreno si muove e la struttura tende a rimanere ferma. In questo caso, il carico dipende dalla massa effettiva, dalla rigidità e dallo smorzamento della struttura e le quantità di interesse sono le accelerazioni, le velocità e gli spostamenti intorno alla struttura. Questa seconda serie di quantità è molto difficile da riprodurre con precisione in laboratorio se non sono disponibili tavole di scuotimento.
Usando la fisica di base, come la Seconda Legge di Newton, si può semplificare il problema dell'equilibrio di una struttura (come un ponte o un telaio con trave rigida), che è soggetta ai moti del suolo (ug),a quello di un singolo grado di libertà di massa(m)con caratteristiche di rigidità(k)e smorzamento(c). Gli ultimi due possono essere rappresentati da una molla in cui la forza è proporzionale allo spostamento (u) e da un dashpot in cui le forze sono proporzionali alla velocità (v) (Figura 1). Questi componenti possono essere combinati in parallelo e/o in serie per modellare diverse configurazioni strutturali.
La rigidità è definita come la forza necessaria per deformare la struttura di una quantità unitaria. Supponiamo che si carichi una trave a sbalzo con una forza nota (P) e si misuri la sua deformazione elastica sulla punta ( 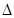 ). La rigidità è definita come k = P/
). La rigidità è definita come k = P/ 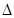 . Per il semplice sistema elastico a sbalzo mostrato, k= L3/3EI, dove L è la lunghezza del cantilever, I è il suo momento di inerzia ed E è il modulo di Young per il materiale utilizzato. Quindi, immagina cosa succede se si rimuove improvvisamente la forza, permettendo così al cantilever di vibrare. Intuitivamente ci si aspetterà che l'ampiezza delle vibrazioni inizi a diminuire ad ogni ciclo. Questo fenomeno è chiamato smorzamento e si riferisce a una serie di complessi meccanismi interni, come l'attrito, che tendono a ridurre le oscillazioni. La quantificazione dello smorzamento è descritta più avanti in questo laboratorio, ma è importante notare che a questo punto non si sa molto su questi meccanismi da un punto di vista teorico o pratico. Un concetto utile è quello di visualizzare il coefficiente di smorzamento critico (ccr), che corrisponde al caso in cui il cantilever si fermi dopo una sola oscillazione completa.
. Per il semplice sistema elastico a sbalzo mostrato, k= L3/3EI, dove L è la lunghezza del cantilever, I è il suo momento di inerzia ed E è il modulo di Young per il materiale utilizzato. Quindi, immagina cosa succede se si rimuove improvvisamente la forza, permettendo così al cantilever di vibrare. Intuitivamente ci si aspetterà che l'ampiezza delle vibrazioni inizi a diminuire ad ogni ciclo. Questo fenomeno è chiamato smorzamento e si riferisce a una serie di complessi meccanismi interni, come l'attrito, che tendono a ridurre le oscillazioni. La quantificazione dello smorzamento è descritta più avanti in questo laboratorio, ma è importante notare che a questo punto non si sa molto su questi meccanismi da un punto di vista teorico o pratico. Un concetto utile è quello di visualizzare il coefficiente di smorzamento critico (ccr), che corrisponde al caso in cui il cantilever si fermi dopo una sola oscillazione completa.
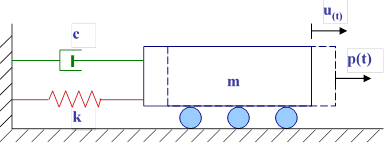
Figura 1: Modello del sistema a grado di libertà singolo.
Scrivere un'equazione di equilibrio orizzontale delle forze per il sistema illustrato nella Figura 1 porta a:
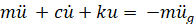 (Eq. 1)
(Eq. 1)
Se guardiamo per un momento un caso più semplice, in cui possiamo ignorare lo smorzamento perché i suoi effetti sono trascurabili e non esiste una funzione di forzatura esterna, l'equazione 1 diventa l'equazione differenziale lineare omogenea del secondo ordine:
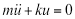 (Eq. 2)
(Eq. 2)
la cui soluzione è della forma:
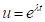 (Eq. 3)
(Eq. 3)
Differenziare due volte ci darà:
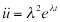 (Eq. 4)
(Eq. 4)
Sostituendo l'equazione 4 nell'equazione 2, si ottiene:
 (Eq. 5)
(Eq. 5)
La soluzione generale è:
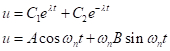 (Eq. 6)
(Eq. 6)
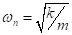 Dov'è la frequenza naturale non smorzata del sistema.
Dov'è la frequenza naturale non smorzata del sistema.
Se a questo sistema viene dato uno spostamento iniziale ( 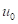 ) e/o una velocità iniziale (
) e/o una velocità iniziale (  ), l'equazione 6 diventa:
), l'equazione 6 diventa:
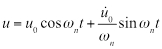 (Eq. 7)
(Eq. 7)
Se aggiungiamo l'effetto dello smorzamento (c) e definiamo  , la frequenza naturale smorzata del sistema diventa
, la frequenza naturale smorzata del sistema diventa 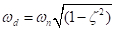 e l'equivalente dell'equazione 7 è:
e l'equivalente dell'equazione 7 è:
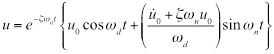 (Eq. 8)
(Eq. 8)
Nel caso di uno spostamento iniziale u0, la Figura 2 mostra il comportamento per diversi valori di  .
.
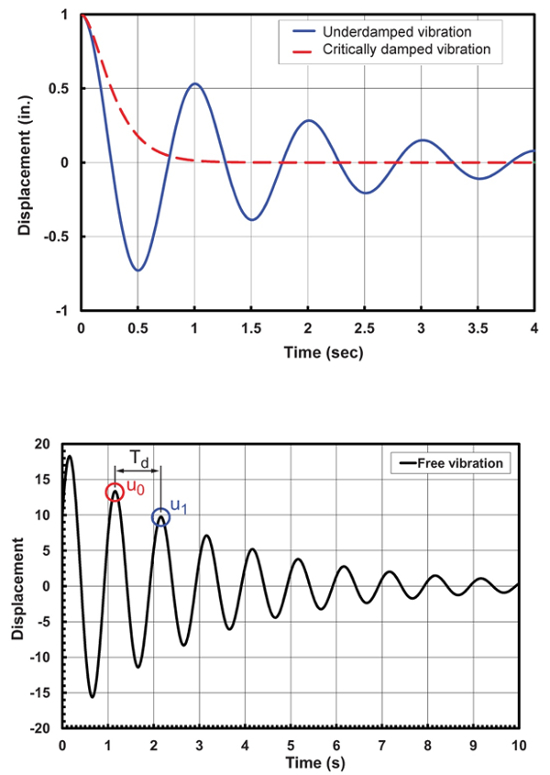
Figura 2: Effetto dello smorzamento sulle vibrazioni libere: definizione di smorzamento critico (superiore); calcolo dello smorzamento da decremento logaritmico (inferiore).
Se nella Figura 2 si definisce  , dove un e un+1 sono lo spostamento in cicli successivi, allora:
, dove un e un+1 sono lo spostamento in cicli successivi, allora:
 (Eq. 9)
(Eq. 9)
Tornando all'equazione 1, se il moto del suolo è preso come funzione sinusoidale  , l'analogo dell'equazione 8 è:
, l'analogo dell'equazione 8 è:
 (Eq. 10)
(Eq. 10)
Dove  è il ritardo di fase e R a è il fattore di risposta di amplificazione, i cui grafici sono illustrati nella Figura 3. La Figura 3 mostra che per bassi valori di smorzamento (
è il ritardo di fase e R a è il fattore di risposta di amplificazione, i cui grafici sono illustrati nella Figura 3. La Figura 3 mostra che per bassi valori di smorzamento (  <0.2), quando la frequenza della funzione di forzatura si avvicina alla frequenza naturale del sistema, la risposta del sistema diventa instabile, un fenomeno che viene comunemente indicato come risonanza.
<0.2), quando la frequenza della funzione di forzatura si avvicina alla frequenza naturale del sistema, la risposta del sistema diventa instabile, un fenomeno che viene comunemente indicato come risonanza.
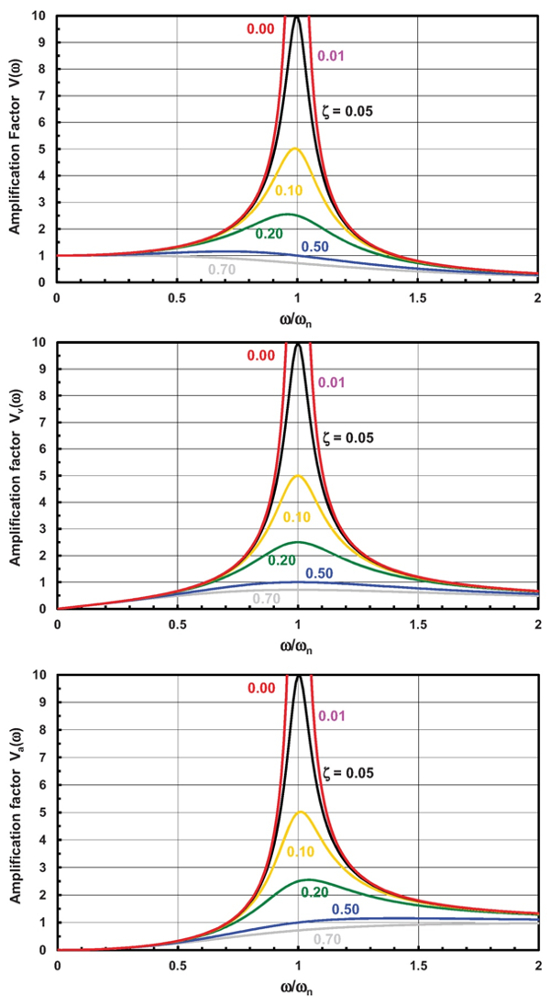
Figura 3: Spostamento, velocità e risposta all'accelerazione.
In questo laboratorio, studieremo sperimentalmente i concetti e le derivazioni alla base delle equazioni 1-10 nel contesto della dinamica delle strutture utilizzando una tavola di scuotimento.
Procedura
1. Modelli
- Per prima cosa costruisci diverse strutture utilizzando travi in alluminio T6011 molto sottili, robuste, rettangolari, 1/32 in. di larghezza e con lunghezze diverse. Per costruire il primo modello, inserire un singolo cantilever con lunghezza di 12 in. su un blocco di legno molto rigido. Posizionare una massa di 0,25 libbre sulla punta del cantilever.
- Allo stesso modo, costruisci altre strutture modello attaccando cantilever con lunghezze diverse allo stesso blocco di legno rigido. Attaccare una massa di 0,25 libbre alla punta di ciascun cantilever.
- Preparare altri due campioni simulando semplici strutture a telaio con colonne flessibili e pavimenti rigidi. Questi possono essere costruiti con sottili piastre di acciaio e diaframmi rigidi acrilici per pavimenti. Una struttura sarà a un piano e l'altra sarà a due piani. I diaframmi del pavimento saranno strumentati con accelerometri.
2. Apparecchio
Per queste dimostrazioni verrà utilizzato un piccolo tavolo da tavolo, azionato elettricamente, azionato a singolo grado di libertà. L'apparato è costituito fondamentalmente da un piccolo tavolo metallico che cavalca su due binari di guida che viene spostato da un motore elettrico. Lo spostamento è controllato digitalmente da un computer in grado di inserire accelerazioni periodiche (onde sinusoidali) o casuali (cronologie temporali preprogrammate di accelerazione del suolo del terremoto). Tutto il controllo avvieni tramite software proprietario o software di tipo MatLab e Si mulLink. La funzione di forzatura dell'ingresso può essere verificata confrontandola con l'uscita di un accelerometro collegato alla tabella.
3. Procedura
- Montare con cura il modello con vari cantilever sul tavolo di scuotimento, utilizzando bulloni attaccati alla base del modello. Accendere il tavolo di agitazione e utilizzando il software, aumentare lentamente la frequenza fino ad ottenere la massima risposta della struttura per ogni cantilever. Si noti che ogni sbalzo entra in risonanza a una particolare frequenza. Registrare in un notebook il valore di questa frequenza. Continuare ad aumentare la frequenza fino a quando gli spostamenti di tutti i cantilever si riducono in modo significativo.
- Montare la struttura del modello a un piano sulla tavola di scuotimento e ripetere la procedura. Scorri lentamente le frequenze fino a raggiungere la risonanza. Reimpostare il software per eseguire una tipica cronologia temporale di accelerazione del terreno (1940 El Centro) per mostrare i movimenti casuali che si verificano durante un terremoto.
- Montare la struttura a due piani sul tavolo di scuotimento e ripetere la procedura. Si noti che in questo caso si verificano due frequenze naturali.
Risultati
Innanzitutto, determinare la frequenza (ω) alla quale si è verificato lo spostamento massimo per ciascun modello. La semplice formula originale discussa sopra,  , deve essere modificata perché la massa del fascio stesso (mb =W beam/g), che è distribuita sulla sua altezza, non è trascurabile rispetto alla massa in alto ( m = Wblock/g). La massa equivalente per il caso di una trave a sbalzo è (m+0,23mb), dove m è la massa nella parte superiore e mb è la massa distribuita della trave. La rigidità k è data dal reciproco della deformazione (
, deve essere modificata perché la massa del fascio stesso (mb =W beam/g), che è distribuita sulla sua altezza, non è trascurabile rispetto alla massa in alto ( m = Wblock/g). La massa equivalente per il caso di una trave a sbalzo è (m+0,23mb), dove m è la massa nella parte superiore e mb è la massa distribuita della trave. La rigidità k è data dal reciproco della deformazione ( 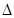 ) causata nella parte superiore del cantilever da una forza unitaria:
) causata nella parte superiore del cantilever da una forza unitaria:
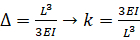 (Eq. 11)
(Eq. 11)
dove L è la lunghezza del fascio, E è il modulo di elasticità e I è il momento di inerzia. I è dato da 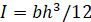 , dove b è la larghezza e h è lo spessore della trave. Pertanto, la frequenza circolare naturale di un raggio a sbalzo, incluso il suo peso personale, è:
, dove b è la larghezza e h è lo spessore della trave. Pertanto, la frequenza circolare naturale di un raggio a sbalzo, incluso il suo peso personale, è:
 (Eq.12)
(Eq.12)
Sulla base di questa equazione, le frequenze naturali previste sono calcolate nella Tabella 1.
| Numero del fascio | Lunghezza (in) |
Larghezza (in.) |
Spesso. (in.) |
Io (in.4) |
E (ksi) |
Peso (libbre) |
Peso del fascio (libbre.) |
Massa effettiva (lbs-sec.2/in) |
Frequenza naturale (cicli al secondo) |
| 1 | 12.0 | 1.002 | 0.124 | 1,59E-04 | 10200 | 0.147 | 0.149 | 4,70E-04 | 2.45 |
| 2 | 16.0 | 1.003 | 0.124 | 1,59E-04 | 10200 | 0.146 | 0.199 | 4,97E-04 | 1.55 |
| 3 | 20.0 | 1.002 | 0.125 | 1,63E-04 | 10200 | 0.146 | 0.251 | 5,28E-04 | 1.09 |
| 4 | 24.0 | 1.003 | 0.125 | 1,63E-04 | 10200 | 0.148 | 0.301 | 5,63E-04 | 0.80 |
| 5 | 28.0 | 1.001 | 0.125 | 1,63E-04 | 10200 | 0.144 | 0.350 | 5,82E-04 | 0.62 |
| 6 | 32.0 | 1.000 | 0.124 | 1,59E-04 | 10200 | 0.146 | 0.397 | 6,15E-04 | 0.49 |
| 7 | 36.0 | 1.002 | 0.126 | 1,67E-04 | 10200 | 0.147 | 0.455 | 6,52E-04 | 0.41 |
| 8 | 40.00 | 1.000 | 0.125 | 1,63E-04 | 10200 | 0.148 | 0.500 | 6,81E-04 | 0.34 |
Tabella 1: Frequenze naturali dei fasci a sbalzo testati.
I valori misurati e teorici della frequenza normale per i nostri sistemi modello sono confrontati nella Tabella 2. Le frequenze naturali effettive sono state calcolate spostando attentamente il raggio a sbalzo di 1 pollice e quindi osservando la risposta di spostamento rispetto al tempo. Il confronto che segue è fatto in termini di periodi (Td , in sec.) in quanto questi sono stati determinati da Td = u0-u1, come mostrato nella Figura 2(b). Ciò richiede cura e pazienza per ottenere risultati affidabili. Le dimostrazioni mostrate avevano solo lo scopo di fornire un'illustrazione generale del comportamento del sistema.
| Numero del fascio | Frequenza naturale (cicli al secondo) |
Periodo previsto (sec.) |
Periodo effettivo (sec.) |
Errore (%) |
| 1 | 2.45 | 2.56 | 2.65 | -3.33% |
| 2 | 1.55 | 4.06 | 4.23 | -4.22% |
| 3 | 1.09 | 5.78 | 6.79 | -17.52% |
| 4 | 0.80 | 7.84 | 8.04 | -2.54% |
| 5 | 0.62 | 10.06 | 10.63 | -5.70% |
| 6 | 0.49 | 12.79 | 13.04 | -1.97% |
| 7 | 0.41 | 15.32 | 16.78 | -9.50% |
| 8 | 0.34 | 18.59 | 20.56 | -10.59% |
Tabella 2. Confronto dei risultati.
Le differenze derivano principalmente dal fatto che le travi non sono rigidamente attaccate alla base in legno e la maggiore flessibilità alla base aumenta il periodo della struttura. Un'altra fonte di errore è che lo smorzamento non è stato contabile nei calcoli, perché lo smorzamento è molto difficile da misurare e l'ampiezza dipende.
Successivamente, da ciascuna delle cronologie di spostamento rispetto a quelle temporali, estrarre il valore massimo per ciascuna frequenza e tracciare l'entità dello spostamento rispetto alla frequenza normalizzata come quella nella Figura 3. Un esempio è mostrato nella Figura 4, dove abbiamo normalizzato la frequenza rispetto alla prima frequenza naturale (Beam Number 1) e tracciato lo spostamento massimo di quel fascio quando la tavola di scuotimento è stata sottoposta a una deformazione sinusoidale variabile con ampiezza di 1 in.

Figura 4: Deformazione del fascio #1 rispetto alla frequenza normalizzata della tabella.
Inizialmente, quando il rapporto tra ω/ωn è piccolo, non c'è molta risposta poiché l'input di energia dal movimento della tabella non eccita il modello. Quando ω/ωn si avvicina a 1, c'è un aumento molto significativo della risposta, con le deformazioni che diventano piuttosto grandi. La risposta massima viene raggiunta quando ω/ωn è molto vicino a 1. Man mano che la frequenza normalizzata aumenta oltre ω/ωn = 1, la risposta dinamica inizia a spegnersi; quando ω/ωn diventa grande ci troviamo in una situazione in cui il carico viene applicato molto lentamente rispetto alla frequenza naturale della struttura, e la deformazione dovrebbe diventare uguale a quella di un carico applicato staticamente.
L'intento di questi esperimenti è principalmente quello di mostrare qualitativamente i cambiamenti nel comportamento, come mostrato nelle dimostrazioni per le due strutture di frame. Ottenere risultati simili a quelli delle Figure 3 e 4 richiede grande cura e pazienza in quanto fonti di attrito e simili influenzeranno la quantità di smorzamento e quindi sposteranno le curve simili a quelle della Figura 3(c) a sinistra o a destra come cambia l'effettiva frequenza smorzata, 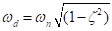 .
.
Applicazione e Riepilogo
In questo esperimento, la frequenza naturale e lo smorzamento di un semplice sistema a sbalzo sono stati misurati utilizzando tabelle di scuotimento. Sebbene il contenuto di frequenza di un terremoto sia casuale e copra una grande larghezza di banda di frequenze, gli spettri di frequenza possono essere sviluppati traducendo la storia del tempo di accelerazione nel dominio della frequenza attraverso l'uso delle trasformate di Fourier. Se le frequenze predominanti del movimento del suolo corrispondono a quelle della struttura, è probabile che la struttura subisca un grande spostamento e di conseguenza sia esposta a gravi danni o addirittura al collasso. La progettazione sismica esamina i livelli di accelerazione previsti da un terremoto in una determinata posizione in base ai record storici, alla distanza dalla fonte del terremoto, al tipo e alle dimensioni della sorgente del terremoto e all'attenuazione della superficie e delle onde corporee per determinare un ragionevole livello di accelerazione da utilizzare per la progettazione.
Ciò di cui il grande pubblico spesso non si rende conto è che le attuali disposizioni di progettazione sismica hanno solo lo scopo di ridurre al minimo la probabilità di collasso e perdita di vite umane nel caso in cui si verifichi un terremoto massimo credibile a un livello accettabile (circa il 5% al 10% nella maggior parte dei casi). Mentre i progetti strutturali per ottenere minori probabilità di fallimento sono possibili, iniziano a diventare antieconomici. Ridurre al minimo le perdite e migliorare la resilienza dopo un tale evento non sono esplicitamente considerati oggi, sebbene tali considerazioni stiano diventando più comuni, poiché molte volte il contenuto di un edificio e la sua funzionalità possono essere molto più importanti della sua sicurezza. Si consideri ad esempio il caso di una centrale nucleare (come Fukushima nel Grande Terremoto del Kanto del 2011), un edificio residenziale di dieci piani a Los Angeles o un impianto di produzione di chip per computer nella Silicon Valley e la loro esposizione e vulnerabilità agli eventi sismici.
Nel caso della centrale nucleare, può essere auspicabile progettare la struttura per ridurre al minimo qualsiasi danno dato che la conseguenza anche di un guasto minimo può avere conseguenze molto disastrose. In questo caso, dovremmo cercare di localizzare questa struttura il più lontano possibile dalle fonti sismiche per ridurre al minimo l'esposizione, perché ridurre al minimo la vulnerabilità al livello desiderato è molto difficile e costoso. La realtà è che è proibitivo farlo dato il desiderio del pubblico di evitare non solo un incidente di tipo Fukushima, ma anche uno più limitato, come il disastro nucleare di Three Mile Island.
Per l'edificio a più piani di Los Angeles, è più difficile ridurre al minimo l'esposizione perché una vasta rete di faglie sismiche con periodi di ritorno in qualche modo sconosciuti si trova nelle vicinanze, inclusa la faglia di San Andreas. In questo caso, l'accento dovrebbe essere posto su un design robusto e sui dettagli per ridurre al minimo la vulnerabilità della struttura; i proprietari delle residenze devono essere consapevoli che stanno correndo un rischio significativo in caso di terremoto. Non dovrebbero aspettarsi che l'edificio crolli, ma l'edificio potrebbe essere una perdita completa se il terremoto è di magnitudo abbastanza grande.
Per l'impianto di chip per computer, i problemi possono essere completamente diversi perché la struttura stessa può essere abbastanza flessibile e al di fuori della gamma di frequenza del terremoto. Pertanto, la struttura non può subire alcun danno; tuttavia, il suo contenuto (apparecchiature per la produzione di chip) potrebbe essere gravemente danneggiato e la produzione di chip potrebbe essere interrotta. A seconda del set specifico di chip prodotti nello stabilimento, il danno economico sia per il proprietario dell'impianto che per l'industria nel suo complesso può essere enorme.
Questi tre esempi illustrano perché è necessario sviluppare strategie di progettazione resilienti per la nostra infrastruttura. Per raggiungere questo obiettivo dobbiamo comprendere sia l'input (movimento del terreno) che l'output (risposta strutturale). Questo problema può essere affrontato solo attraverso un approccio analitico e sperimentale combinato. Il primo si riflette nelle equazioni sopra elencate, mentre il secondo può essere raggiunto solo attraverso il lavoro sperimentale svolto attraverso approcci quasi-statici, pseudo-dinamici e shake table.
Vai a...
Video da questa raccolta:

Now Playing
Dinamica delle strutture
Structural Engineering
11.5K Visualizzazioni

Costanti dei materiali
Structural Engineering
23.5K Visualizzazioni

Caratteristiche sforzo-deformazione degli acciai
Structural Engineering
110.3K Visualizzazioni

Caratteristiche sforzo-deformazione dell'alluminio
Structural Engineering
89.1K Visualizzazioni

Test di impatto Charpy di acciai formati a freddo e laminati a caldo in diverse condizioni di temperatura
Structural Engineering
32.4K Visualizzazioni

Prova di durezza Rockwell e l'effetto del trattamento sull'acciaio
Structural Engineering
28.4K Visualizzazioni

Instabilità delle colonne d'acciaio
Structural Engineering
36.2K Visualizzazioni

Fatica dei metalli
Structural Engineering
41.2K Visualizzazioni

Prova di trazione di materiali polimerici
Structural Engineering
25.6K Visualizzazioni

Prova di trazione di materiali polimerici fibrorinforzati
Structural Engineering
14.6K Visualizzazioni

Aggregati per calcestruzzo e miscele bituminose
Structural Engineering
12.2K Visualizzazioni

Prove su calcestruzzo fresco
Structural Engineering
25.8K Visualizzazioni

Prove di compressione su calcestruzzo indurito
Structural Engineering
15.2K Visualizzazioni

Prove di calcestruzzo indurito in trazione
Structural Engineering
23.5K Visualizzazioni

Prove su legno
Structural Engineering
33.0K Visualizzazioni