Aby wyświetlić tę treść, wymagana jest subskrypcja JoVE. Zaloguj się lub rozpocznij bezpłatny okres próbny.
Method Article
Setting Limits on Supersymmetry Using Simplified Models
W tym Artykule
Podsumowanie
This paper demonstrates a protocol for recasting experimental simplified model limits into conservative and aggressive limits on an arbitrary new physics model. Publicly available LHC experimental results can be recast in this manner into limits on almost any new physics model with a supersymmetry-like signature.
Streszczenie
Experimental limits on supersymmetry and similar theories are difficult to set because of the enormous available parameter space and difficult to generalize because of the complexity of single points. Therefore, more phenomenological, simplified models are becoming popular for setting experimental limits, as they have clearer physical interpretations. The use of these simplified model limits to set a real limit on a concrete theory has not, however, been demonstrated. This paper recasts simplified model limits into limits on a specific and complete supersymmetry model, minimal supergravity. Limits obtained under various physical assumptions are comparable to those produced by directed searches. A prescription is provided for calculating conservative and aggressive limits on additional theories. Using acceptance and efficiency tables along with the expected and observed numbers of events in various signal regions, LHC experimental results can be recast in this manner into almost any theoretical framework, including nonsupersymmetric theories with supersymmetry-like signatures.
Wprowadzenie
One of the most promising extensions of the Standard Model, supersymmetry (SUSY)1-14, is the central focus of many searches by the LHC experiments at CERN. The data collected in 2011 are already sufficient to push the limits of new physics beyond those of any previous collider15-22. As new data arrive and the exclusions are pushed still farther, it will be increasingly important to clearly communicate to the physics community what regions of the extensive supersymmetric parameter space have been excluded. Current limits are typically set on constrained two-dimensional planes, which frequently do not represent the diverse available SUSY parameter space and are difficult to understand as limits on physical masses or branching fractions. A large set of simplified models23, 24 have been proposed for aiding in the understanding of these limits, and both ATLAS and CMS have provided exclusion results for several of these models15-20.
This paper demonstrates the application of these simplified model exclusions to a full new physics model using the example of the minimal supergravity (MSUGRA, also known as the CMSSM)25-30. This model is chosen in order to compare the limits set using simplified models to those published independently by the experiments. The procedure is sufficiently general to be extendable to any new physics model (NPM). As this represents the first attempt to "close the loop" and set limits on SUSY using simplified models, a number of assumptions about the applicability of limits on particular simplified models are explored, resulting in recipes for setting conservative and aggressive limits on theories that have not been examined by the LHC experiments.
For setting a limit in a NPM, three separate operations are required. First, the NPM must be deconstructed into its constituent pieces, separating the various production modes and decay modes for all new particles in the model. Second, a set of simplified models must be chosen to recreate the kinematics and relevant event topologies in the NPM. Third, the available limits on these simplified models must be combined in order to produce limits on the NPM. These three procedures are described in the protocol. Some additional approximations are also provided that may expand the applicability of the already-available simplified models to a broader range of event topologies.
A complete NPM typically involves many production modes and many possible subsequent decays. The deconstruction of new physics models into their components and the application of simplified model limits to those components allows the construction of an exclusion limit directly. For any signal region, the most conservative limit can be set using the production fraction P(a,b) (where a,b represents the simplified model sparticle production mode) of events identical to a simplified model i and the branching fraction for the produced sparticles to decay in the manner described by the simplified model†, BRa→ i x BRb → i. The expected number of events in a given signal region from these simple topologies can then be written as
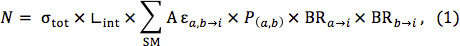
where the sum is over simplified models, σtot is the total cross section for the NPM point, Lint is the integrated luminosity used in the search, and AEa,b → i is the acceptance times efficiency for the simplified model events in the signal region being considered. This number can be compared to the expected 95% confidence level upper limit on the number of new physics events to select the optimal search region. The model can then be excluded if N is larger than the observed number of new physics events excluded at the 95% confidence level. Exclusions in nonoverlapping regions may be combined if information about the correlations of their uncertainties is available. If this information is not available, the best signal region or analysis that provides the best expected limit can be used to attempt to exclude the model.
In order to construct concrete limits with this method, the Aε for various simplified models must be made available by the LHC experiments. Both CMS and ATLAS have published figures with the Aε for several models, and a few of the figures are available in the HepData database31. In order to demonstrate the value of publishing all such tables, we feel it is important to provide concrete limits that are comparable to those already published. Therefore we use (and describe in the protocol as an optional step) a fast detector simulation to emulate the effect of the ATLAS or CMS detector. The Aε derived from the Pretty Good Simulation (PGS)32 is compared to that published by ATLAS in a simplified model grid in Figure 1. These results are sufficiently close to one another (within roughly 25%) that, rather than wait for all results to be public, Aε results for the remaining grids are derived using PGS and used directly in the remainder of this paper. As the number of publicly available simplified model Aε results grows, the need for such approximations should be significantly reduced.
Two conservative assumptions allow the inclusion of a larger number of production and decay modes in the limit. The first is that for associated production the experimental Aε is at least as high as the Aε for the worse of the two production modes. For inclusive searches, this is generally a good assumption. The minimum expected number of events would then be
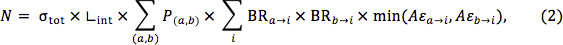
where the first sum runs over all production modes, and only those where a and b are exactly those particles from the simplified model are included in Equation 1. Similarly, the Aε for decays with different legs can be assumed to be at least as high as the Aε for the worse of the two legs. That is,
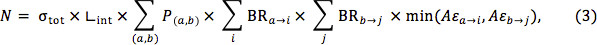
where diagrams with different decays on either side have now been included.
Two further assumptions would allow the setting of stricter limits. One can assume that the experimental Aε for all production modes in the theory is similar to the average Aε for the production modes covered by simplified models. In that case, the expected number of events can instead be written as
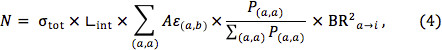
where the sums are both over only those production modes covered by simplified models. One might further assume that the Aε for all decay modes in the theory is similar to the average Aε for those events covered by the simplified model topologies. Then the expected number of events may be written as:
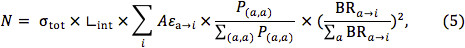
where again the sums run only over the simplified models. Clearly, the most aggressive MSUGRA limit is provided under this assumption, and a limit set in this manner risks claiming exclusion for regions that would not, in fact, be excluded at the 95% confidence level by a dedicated search. Although the accuracy of these two approximations might be suspect, if the inclusive event kinematics of the simplified models compare favorably to a complete SUSY parameter space point, they may not be unreasonable.
† Some simplified models now used at the LHC include associated production. While not explicitly discussed here, the equations can be trivially extended to allow for this case.
Protokół
1. Model Deconstruction
- Generate proton-proton collision events covering a plane in the parameter space of the NPM. Any event generator configuration that includes a parton shower and hadronization model can be used. In the case of MSUGRA for example, the mass spectra are generated using Isasugra33, and the branching fractions and decay widths are calculated using MSSMCalc34. For the event generation itself, MadGraph 5 1.3.934 with CTEQ 6L1 parton density functions35 is used to generate matrix-element events, since it includes additional radiation in the matrix element, which can be important for small mass-splitting scenarios. In order to mimic the LHC experiments' choices of leading-order generators for MSUGRA, the additional radiation in the MadGraph matrix element is disabled when generating MSUGRA events. Pythia 6.42536 is then used for SUSY particle (sparticle) decay, parton showering, and hadronization. Extensive documentation for any of these programs is readily available on the web.
- In order to mimic an LHC detector, pass the events through PGS with an LHC-detector parameter card. The ATLAS and CMS detector cards included with MadGraph 534 perform well enough for search reach analysis. Where available, the experiments' parameterizations of identification and performance made public with some analyses can be used. Ideally, the experiments will provide full maps of acceptance and efficiency for a number of simplified model grids, in which case these can be used directly and this step is unnecessary.
- In order to analyze the results quickly, an intermediate light-weight data format is desirable. Extracting the jets, stable leptons, missing transverse energy, and any other necessary final-state objects from the PGS output (e.g. using ExRootAnalysis34) in a convenient format is recommended.
- In order to classify the results, correlate the PGS event results with the portion of the generator event record necessary to classify the sparticle production and decay modes for each event. Keep track of all particle masses, production mechanisms, and decay chains as well as their respective counts in order to be able to calculate their corresponding branching fraction.
- Calculate the best available production cross-section calculations for the model of interest. In the case of MSUGRA, next-to-leading order cross-sections for each point can be calculated using Prospino 2.137 with NLL-Fast38 using CTEQ 6.6 NLO PDFs.
2. Model Reconstruction
- Based on the breakdown from the model deconstruction, choose a dictionary of simplified models so as to cover at least 50% of the open production and decay modes of the NPM. Because of the rapidly falling cross-section of most BSM models with mass, a factor of two in acceptance typically represents only 20-50 GeV in the limit, making this sufficiently close to be within the experimental and theoretical uncertainties. Most direct decay and one-step decay models, including off-shell/three-body decays, have been considered by the LHC experiments. CMS has collected a number of simplified model exclusion results in a single paper21. Both ATLAS and CMS have also considered a number of heavy-flavor simplified models. The full list of models has not been made publicly available in a single place. However, the results are available from the two experiments' public webpages39, 40. These are the simplified models that should be selected from for reconstruction of the NPM.
- In order to test the quality of the simplified model coverage, compare the kinematics of a few representative NPM points with those resulting from the simplified models used to reproduce that point. For a given NPM point, construct the relevant simplified models with the appropriate masses.
- Assign a weight to each model type that includes the production fraction represented by that simplified model times the branching fraction for the decay represented by that model.
- For associated production, if only pair-production simplified models are considered, divide the weight between the two relevant simplified models.
- It is recommended to apply a set of physically-motivated simplifications to the NPM event topologies in order to group similar production- and decay-modes.
- Normalize the sum of the weights for all the simplified models to unity.
- Calculate the kinematic distributions for the representative NPM points using the event generation procedure described in the previous protocol.
- If the kinematics of the NPM point after typical signal selections differ by more than σ (30%) from those of the combined simplified models, include additional simplified models to improve the production and decay phase-space coverage. Discrepancies on the 15% level have negligible impact on the final exclusion results because of the rapidly falling cross-sections in most new physics models.
3. Limit Construction
- Obtain the available and relevant Aε and 95% confidence level upper limit on the number of new physics events for the simplified models being considered in each experimental signal region that can be applied.
- Apply Equations 1 and 3-5 to the NPM of interest at each parameter space point to determine under which (if any) assumptions the point is excluded.
- Use the limit set by the signal region with the best expected performance, unless correlations between the signal regions' background uncertainties are available so that the regions can be properly combined‡.
- With the comparison of kinematics performed with the previous protocol and the spread of the exclusion contours, determine the range in which the experimental exclusion should lie.
‡ At present, no such correlations are available.
Wyniki
Having applied the model deconstruction step to a point in the parameter space of MSUGRA, a breakdown of the output can be best visualized by counting up the various production and decay modes for every generated event and plotting the corresponding production rates and branching fractions according to the relative frequencies. The branching fractions for the various production and decay modes for representative MSUGRA points are illustrated in Figures 2 and 3. A large number of similar ...
Dyskusje
The application of simplified model limits to produce an exclusion contour in a complete new physics model has been demonstrated. Despite the apparent complexity of MSUGRA parameter space points, the kinematics can be well-reproduced by a combination of only a small number of simplified models. The kinematic agreement is further improved when looking within a particular signal region, since the searches thus far conducted at the LHC tend to favor simplified model-like event topologies with a (relatively) small number of ...
Ujawnienia
The authors are both members of the ATLAS Collaboration. However, no ATLAS internal resources, monetary or otherwise, were used in the completion of this work.
Podziękowania
The authors would like to thank Jay Wacker for significant discussion of simplified models and potential pitfalls. Many thanks also to Max Baak and Till Eifert for constructive criticism and encouragement whenever it was necessary. Thanks to the CERN Summer Student Program for making this collaboration possible.
Odniesienia
- Miyazawa, H. Baryon Number Changing Currents. Prog. Theor. Phys. 36, 1266-1276 (1966).
- Ramond, P. Dual Theory for Free Fermions. Phys. Rev. D. 3, 2415-2418 (1971).
- Gol'fand, Y. A., Likhtman, E. P. Extension of the Algebra of Poincare Group Generators and Violation of P invariance. JETP Lett. 13, 323-326 (1971).
- Neveu, A., Schwarz, J. H. Factorizable dual model of pions. Nucl. Phys. B. 31, 86-112 (1971).
- Gervais, J. L., Sakita, B. Field theory interpretation of supergauges in dual models. Nucl. Phys. B. 34, 632-639 (1971).
- Neveu, A., Schwarz, J. H. Quark Model of Dual Pions. Phys. Rev. D. 4, 1109-1111 (1971).
- Volkov, D. V., Akulov, V. P. Is the neutrino a goldstone particle. Phys. Lett. B. 46, 109-110 (1973).
- Wess, J., Zumino, B. A lagrangian model invariant under supergauge transformations. Phys. Lett. B. 49, 52-54 (1974).
- Wess, J., Zumino, B. Supergauge transformations in four dimensions. Nucl. Phys. B. 70, 39-50 (1974).
- Fayet, P. Supersymmetry and Weak, Electromagnetic and Strong Interactions. Phys. Lett. B. 64, 159-162 (1976).
- Fayet, P. Spontaneously Broken Supersymmetric Theories of Weak, Electromagnetic and Strong Interactions. Phys. Lett. B. 69, 489-494 (1977).
- Farrar, G. R., Fayet, P. Phenomenology of the Production, Decay, and Detection of New Hadronic States Associated with Supersymmetry. Phys. Lett. B. 76, 575-579 (1978).
- Fayet, P. Relations Between the Masses of the Superpartners of Leptons and Quarks, the Goldstino Couplings and the Neutral Currents. Phys. Lett. B. 84, 416-420 (1979).
- Dimopoulos, S., Georgi, H. Softly Broken Supersymmetry and SU(5. Nucl. Phys. B. 193, 150-162 (1981).
- The ATLAS Collaboration. Search for squarks and gluinos with the ATLAS detector in final states with jets and missing transverse momentum using 4.7 fb-1 of √s = 7TeV proton-proton collisions. Phys. Rev. D. , .
- The ATLAS Collaboration. Search for squarks and gluinos using final states with jets and missing transverse momentum with the ATLAS detector in √s = 7TeV proton-proton collisions. Phys. Lett. B. 710, 67-85 (2012).
- The ATLAS Collaboration. Further search for supersymmetry at √s=7 TeV in final states with jets, missing transverse momentum and isolated leptons with the ATLAS detector. Phys. Rev. D. , .
- The CMS Collaboration. Search for new physics in the multijet and missing transverse momentum final state in proton-proton collisions at sqrt(s) = 7 TeV. Phys. Rev. Lett. 109, 171803 (2012).
- The CMS Collaboration. Search for supersymmetry in pp collisions at √s=7 TeV in events with a single lepton, jets, and missing transverse momentum. J. High Energy Phys. 08, 165 (2011).
- The CMS Collaboration. Search for supersymmetry in events with b-quark jets and missing transverse energy in pp collisions at 7 TeV. Phys. Rev. D. 86, 072010 (2012).
- The CMS Collaboration. 2012 Report No.: CMS-PAS-SUS-11-016. Interpretation of Searches for Supersymmetry. , (2012).
- The CMS Collaboration. Search for new physics in events with opposite-sign leptons, jets, and missing transverse energy in pp collisions at sqrt(s = 7 TeV. Phys. Lett. B. 718, 815 (2012).
- Alves, D., et al. Where the Sidewalk Ends: Jets and Missing Energy Search Strategies for the 7 TeV LHC. JHEP. 1110, 012 (2011).
- Alves, D., et al. Simplified Models for LHC New Physics Searches. J. Phys. G.: Nucl. Part. Phys. 39, 105005 (2012).
- Chamseddine, A. H., et al. Locally Supersymmetric Grand Unification. Phys. Rev. Lett. 49, 970-974 (1982).
- Barbieri, R., et al. Gauge models with spontaneously broken local supersymmetry. Phys. Lett. B. 119, 343-347 .
- Ibanez, L. E. Locally supersymmetric SU(5) grand unification. Phys. Lett. B. 118, 73 (1982).
- Hall, L. J., et al. Supergravity as the messenger of supersymmetry breaking. Phys. Rev. D. 27, 2359-2378 (1983).
- Ohta, N. Grand Unified Theories Based on Local Supersymmetry. PTP. 70, 542-549 (1983).
- Chung, D. J. H., et al. The soft supersymmetry-breaking Lagrangian: theory and applications. J. Phys. Rept. 407, 1-203 (2005).
- Alwall, J. MadGraph 5: Going Beyond. JHEP. 1106, 128 (2011).
- Pumplin, J. New Generation of Parton Distributions with Uncertainties from Global QCD Analysis. JHEP. 0207, 012 (2002).
- Sjöstrand, T., Mrenna, S., Skands, P. Pythia 6.4 Physics and Manual. JHEP. 05, 026 (2006).
- . PhysicsResultsSUS < CMSPublic < TWiki [Internet] Available from: https://twiki.cern.ch/twiki/bin/view/CMSPublic/PhysicsResultsSUS
- . SupersymmetryPublicResults < AtlasPublic < TWiki [Internet] Available from: https://twiki.cern.ch/twiki/bin/view/AtlasPublic/SupersymmetryPublicResults (2013)
- Collaboration, D. 0. Search for Squarks and Gluinos in pp̄ collisions at √s=1.8TeV. Phys. Rev. Lett. 75, 618-623 (1995).
- Collaboration, C. D. F. Search for Gluinos and Scalar Quarks in pp̄ collisions at √s=1.8TeV using the Missing Energy plus Multijets Signature. Phys. Rev. Lett. 88, 041801 (2002).
- Collaboration, C. D. F. Inclusive Search for Squark and Gluino Production in pp̄ Collisions at√s=1.96TeV. Phys. Rev. Lett. 102, 121801 (2009).
- Collaboration, D. 0. Search for squarks and gluinos in events with jets and missing transverse energy using 2.1fb-1 of pp̄ collision data at √s=1.96TeV. Phys. Lett. B. 660, 449-457 (2008).
- Collaboration, D. E. L. P. H. I. Searches for supersymmetric particles in e+e-collisions up to 208 GeV and interpretation of the results within the MSSM. Eur. Phys. J. C. 31, 421-479 (2003).
- Collaboration, L. 3. Search for Scalar Leptons and Scalar Quarks at LEP. Phys. Lett. B. 580, 37-49 (2004).
- Collaboration, A. T. L. A. S. Search for squarks and gluinos using final states with jets and missing transverse momentum with the ATLAS detector in √s=7TeV proton-proton collisions. Phys. Lett. B. 701, 186-203 (2011).
Przedruki i uprawnienia
Zapytaj o uprawnienia na użycie tekstu lub obrazów z tego artykułu JoVE
Zapytaj o uprawnieniaThis article has been published
Video Coming Soon
Copyright © 2025 MyJoVE Corporation. Wszelkie prawa zastrzeżone