Белки МУДРОСТЬ Workbench для<em&gt; В кремнии</em&gt;<em&gt; De Novo</em&gt; Дизайн биомолекул

Резюме

We developed computational de novo protein design methods capable of tackling several important areas of protein design. To disseminate these methods we present Protein WISDOM, an online tool for protein design (http://www.proteinwisdom.org). Starting from a structural template, design of monomeric proteins for increased stability and complexes for increased binding affinity can be performed.

Аннотация

Целью де конструкции белка заново, чтобы найти аминокислотных последовательностей, которые складываются в желаемый 3-мерные структуры с улучшением конкретные свойства, такие как аффинность связывания, агонист или антагонист поведение, или стабильность, по сравнению с нативной последовательностью. Белкового дизайна лежит в центре текущих наркотиков достижениями дизайна и открытий. Мало того, что белка конструкции обеспечивают прогнозы на потенциально полезных лекарственных препаратов, но и усиливает наше понимание процесса сворачивания белков и белок-белковых взаимодействий. Экспериментальные методы, такие как направленной эволюции привели к успешному белок конструкции. Однако такие способы ограничены ограниченном пространстве последовательности, которые можно найти tractably. В противоположность этому, вычислительные стратегии конструкция позволяет для скрининга гораздо большего множества последовательностей, охватывающий широкий спектр свойств и функциональных возможностей. Мы разработали ряд вычислительных De Novo белкового дизайна метоDS, способной решать несколько важных областях проектирования белка. Они включают в себя дизайн мономерных белков для повышения стабильности и комплексы повышенной аффинностью связывания.

Распространение этих методов для широкого использования данного белка мы мудрости ( http://www.proteinwisdom.org ), инструмент, который обеспечивает автоматизированных методов целый ряд проблем проектирования белка. Структурные шаблоны представленные для инициализации процесса проектирования. Первый этап дизайн оптимизации выбора последовательности этап, который направлен на повышение стабильности путем минимизации потенциальной энергии в пространстве последовательностей. Выбранный последовательности затем проходят через стадию раза специфичностью и сродством обязательного этапа. Ранга упорядоченный список последовательностей для каждого этапа процесса, наряду с соответствующими предназначенный структур, предоставляет пользователю всеобъемлющей количественной оценки конструкции. Здесь мы предлагаем подробно ое каждый метод расчета, а также несколько известных экспериментальных успехи, достигнутые за счет использования методов.

Введение

De novo protein design is the identification of protein sequences that will yield a desired tertiary structure with improved properties or function. Since the native fold of a protein is the conformation which lies at the free energy minimum, de novo protein design seeks sequences that will have a free energy minimum in the target fold. This problem was first described by Drexler¹ and Pabo² and was referred to as the "inverse folding problem." However, unlike the protein folding problem, where a sequence can yield only one folded structure solution, the de novo protein design problem exhibits degeneracy. Many different amino acid sequences can yield the same tertiary structure and function.

While protein design has traditionally been performed experimentally through rational design and directed evolution, computational methods have more recently been employed to overcome the limited search space inherent in experimental methods. A variety of computational methods have been used, including deterministic methods, stochastic methods, and probabilistic methods.^3,4 Early computational methods used fixed-backbone templates to make the problem easier to solve.^5-7 With the advent of faster processors, high performance computing, and more efficient algorithms, backbone flexibility has been incorporated by using an ensemble of fixed-backbone templates^8-14 or by incorporating true backbone flexibility by expressing the template in terms of ranges of atom-to-atom distances and dihedral angles.^15,16

This paper describes in detail Protein WISDOM, an online tool that has been made available to the academic community to utilize our computational de novo protein design framework. This framework has been applied to the design of numerous proteins, for therapeutic use targeting diseases such as HIV, cancer, complement diseases, and other autoimmune disorders. Many of the predicted peptides were experimentally validated, demonstrating the power of the method. Table 1 provides a summary of the different proteins that have been designed including the size of the protein or peptide, the number of predictions, and experimental validation.

Protein Design	Protein Length	# of Computational Predictions	# of Experimental Validations	Reference
Full sequence design of human beta-defensin-2	41	340		(17)
Compstatin inhibitors of human C3	13	28	3/3	(18, 19)
Compstatin analogues that bind to rat C3c	13	5		(20)
Compstatin analogues with di-serine extension	15	8
Stabilizing structure of compstatin analog W4A9	13	18
C3a receptor agonists and antagonists	77	20	4/7	(21)
C5a receptor agonists and antagonists	74	61	2/61
HIV-1 gp14 inhibitors	12	6	4/5	(22)
HIV-1 gp120 inhibitors	9	14
Bak inhibitors of Bcl-x L and Bcl-2	16-18	10	5/5	(23)
Inhibitors of ERK2	11	25
Inhibitors of EZH2	21	17	10/10	(24)
Inhibitors of LSD1 and LSD2	16	41	17/20
Inhibitors of HLA-DR1	13	6		(25)
Inhibitors of PNP	5	13

Table 1. Summary of designed proteins and peptides using the de novo protein design framework. The # of computational predictions is presented as the number of favorable predictions (i.e. fold specificities above a certain cutoff or approximate binding affinities greater than the native sequence). The # of experimental validations gives two numbers: the first is the number of predictions that were experimentally validated while the second is the total number of predictions that were tested experimentally.

Design of human-beta-defensin-2 (hβD-2) was performed to enhance the peptide's antimicrobial property.¹⁷ For this design, we considered two cases: 1) up to 10 mutations along hβD-2 and 2) full sequence design of all hβD-2 residue positions except the Cysteines (8, 15, 20, 30, 37, and 38). Three different design templates and three different sequence selection models were utilized in the design. High levels of similarity in mutations were observed between the weighted average and distance bin models for both the 10 mutation design and the full sequence design. Additionally, a large number of sequences were found to have more favorable calculated Fold Specificity values than the native sequence.

Complement system inhibitors (of C3, C3a, and C5a) were designed to combat a number of immune diseases such as stroke, heart attack, Alzheimer's disease, asthma, rheumatoid arthritis, rejection of xenotransplantation, adult respiratory disease, psoriasis, and Crohn's disease. Three compstatin inhibitors of C3c predicted by the protein design framework plus three rationally designed sequences were experimentally validated to be better binders than the native compstatin.^18,19

Further studies examined the loss of activity of compstatin against non-primate C3c and designed a number of candidate rat and mouse C3c inhibitors. Five sequences were shown to have more favorable association free energies with rat C3c than the W4A9 compstatin mutant known to inhibit C3c. This is due to a new salt bridge formation by Arg1.²⁰ Eight sequences with an N-terminal extension were predicted to be better binders than W4A9 with a di-Serine extension. Finally, 18 compstatin sequences were predicted to stabilize the bound conformation of W4A9, providing strong candidates for primate and non-primate C3c inhibitors.

In addition to C3c inhibitors, C3a and C5a receptor agonists and antagonists were designed based upon the structures of C3a and C5a. Seven C3a sequences predicted by the model were experimentally tested. Two of the sequences were potent agonists while two others were partial agonists.²¹ The two potent agonists showed a 58-fold improvement over a previously discovered "superagonist". The design of C5a receptor agonists and antagonists provided a set of 61 sequences. All the sequences were synthesized and two were found to be novel C5a agonists.

Fusion inhibitors of HIV-1, the virus that causes AIDS, were designed to prevent HIV-1 from infecting cells. The first design targeted gp41, an envelope glycoprotein of HIV-1. The protein design framework predicted six sequences that were better binders than the native sequence. Four of these predicted sequences were experimentally validated to inhibit HIV-1 with the best sequence having an IC₅₀ as low as 29 μM. This sequence showed a 3-15 fold improvement over the native sequence and had no loss of activity against an Enfuvirtide-resistant virus strain.²² The second design targeted gp120, another envelope glycoprotein of HIV-1. Fourteen sequences were predicted to be binders of gp120 and provide additional potential fusion inhibitors of HIV-1.

Numerous proteins linked to cancer provided promising targets for cancer therapeutics. Bcl-2 and Bcl-x_L are anti-apoptotic proteins that prevent cell death. Inhibitors of these two proteins were designed to induce cell death in cancer cells. Ten sequences were predicted to be better binders than the native, and these results captured previous experimental and mutagenesis results.²³ Another target protein, ERK2, is involved in signal-transduction cascades that make it a promising target for antiproliferative cancer therapies. Twenty-five sequences were predicted to be inhibitors of ERK2.

Histone methyltransferases and demethylases dynamically control histone methylation, which has been linked to many cancer types including prostate, breast, lymphoma, myeloma, bladder, colon, skin, liver, endometrial, lung, and gastric. The de novo protein design framework identified 17 inhibitors of EZH2 (a Lysine methyltransferase) and of the ten experimentally tested, all were found to inhibit EZH2.²⁴ The most potent peptide had an IC₅₀ of about 13 μM, was equally effective with elevated enzyme concentrations, and did not compete with the cofactor. These peptides were the first set of inhibitors of EZH2. 53 inhibitors of LSD1 (a demethylase) were predicted by the framework and of the 20 experimentally tested, 17 were inhibitors of LSD1 and 18 were inhibitors of LSD2. The best inhibitors had IC₅₀ values below 1 μM, making them the most potent peptidic inhibitors discovered to date.

The final two protein systems provided targets for treating various autoimmune diseases such as Coeliac disease, diabetes mellitus type 1, systemic lupus erythematosus, Sjögren's syndrome, Churg-Strauss Syndrome, Hashimoto's thyroiditis, Graves' disease, idiopathic thrombocytopenic purpura, rheumatoid arthritis, and allergies. None of these potential inhibitors have been experimentally validated, however the framework predicted six sequences that bind to HLA-DR1 and 13 sequences that bind to PNP.

Table 2 summarizes experimentally validated inhibitors and agonists predicted using the de novo protein design framework. The approximate binding affinity metric was used to predict nine of the sequences (inhibitors of human C3c, HIV-1 gp41, EZH2, LSD1, and LSD2), while the fold specificity metric was used to identify four of the sequences (agonists/antagonists of C3aR). These peptides highlight the success of the de novo protein design framework, particularly the added approximate binding affinity metric. The framework is extremely versatile in its applicability. Six different proteins linked to twenty-five different diseases have been successfully designed and experimentally validated.

Name	IC50	EC50	Protein Target	Applicable Diseases
SQ027	0.94 μM		human C3c	stroke, heart attack, Alzheimer's disease, asthma, rheumatoid arthritis, systemic lupus erythematosus, multiple sclerosis, psoriasis, diabetes type I, Crohn's disease, pancreatitis, and cystic fibrosis
SQ086	1.98 μM		human C3c
SQ059	4.73 μM		human C3c
SQ110-4		15.2 nM	C3aR
SQ060-4		36.4 nM	C3aR
SQ007-5	15.4 nM		C3aR
SQ002-5	26.1 nM		C3aR
SQ435	29 - 253 μM		HIV-1 gp41	AIDS
SQ037	13.57 μM		EZH2	prostate, breast, lymphoma, myeloma, bladder, colon, skin, liver, endometrial, lung, and gastric cancers
SQ011-1	0.521 μM		LSD1
SQ016-1	0.249 μM		LSD1
SQ026-1	2.51 μM		LSD2
SQ015-1	1.332 μM		LSD2

Table 2. Computationally predicted and experimentally validated peptides targeting various diseases.

протокол

Method Overview

The de novo design framework used in Protein WISDOM consists of two stages. The first stage produces a rank-ordered list of amino acid sequences that will fold into a given template structure. The second stage validated these sequences by calculating either fold specificity or approximate binding affinity, or both. The former is primarily used when the design is of a single protein, while the latter is used when the design is of a complex (a peptide binding to a target protein). Figure 1 gives an overview of the steps involved in the framework.

Design Inputs: A number of inputs need to be defined for the de novo protein design framework. The first is the design template. This is a 3-dimensional (3D) protein structure that contains coordinates for all the atoms in the protein. The structure can be rigid or flexible. Rigid templates are a set of fixed atom coordinates and are obtained from x-ray crystallography structures. Flexible templates can be a set of fixed atom coordinates or upper and lower bounds on the atom coordinates. These templates can be obtained from NMR solution structures, molecular dynamics, or docking simulations.

The design template is used to generate the allowed mutation set of the designed protein. This set defines which positions of the sequence can mutate and to what amino acids. The mutation set is generated by calculating the solvent accessible surface area (SASA) of each residue in the design template. If the residue is more than 50% exposed to solvent, a set of hydrophilic amino acids is allowed (D, E, G, H, K, N, P, Q, R, S, T). If the residue is less than 20% exposed to solvent, a set of hydrophobic amino acids is allowed (A, F, I, L, M, V, W, Y). If the residue's exposure is in between 20% and 50%, all amino acids are allowed. Cysteine is typically excluded from the mutation set unless experimental or literature data deem it appropriate. The small amino acids (A, G, T) are typically included in all mutation sets. When available, experimental or literature insights can be used to manually modify the mutation sets of particular amino acid positions.

A forcefield is chosen to calculate the pairwise interaction energy of the sequences in the design template. While any forcefield can be adapted to be used within the framework, two distance-dependent forcefields have been developed and are used extensively in the de novo design framework. The first is a high resolution C^α-C^α forcefield,²⁶ where the distances are between the C^α carbons of the residues. The second is a high resolution centroid-centroid forcefield²⁷ where the distances are between the centroids of the residues. The energy parameters in the forcefields were derived by solving a linear programming parameter estimation problem which required the low-energy high-resolution decoys for a large training set of proteins to be energetically less favorable than their native conformations. The high-resolution centroid-centroid forcefield and the C^α-C^α forcefield were both tested and validated in previous studies on human beta-defensin-2.¹⁷ True backbone flexibility is incorporated into the model by discretizing the forcefields into distance bins. The distance between a pair of amino acids will correspond to a distance bin giving the same energy value to a range of distances. This enables the sequence selection optimization model to account for backbone movement.

Biological constraints, in the form of charge constraints or content constraints, can be included manually by the user as an additional design input. Charge constraints specify a particular charge or range of charges that must be satisfied for the designed sequence or a portion of the designed sequence. The charge is calculated as the sum of the positively charged residues (K and R) minus the sum of the negatively charged residues (D and E). Content constraints specify upper and lower bounds on the occurrence of a particular amino acid in the sequence. Biological Constraints are generally defined through an extensive sequence alignment to the native sequence. This is to capture the known biological limits on charge and amino acid content represented in nature for a family of proteins. Further constraints are manually defined through analysis of known experimental data.

Stage One: Sequence Selection: The original sequence selection method was first developed by Klepeis et al.^15,16 It selects and ranks amino acid sequences according to their energies in the design template using an Integer Linear Optimization (ILP) model. The method was later improved by the use of a more computationally efficient sequence selection model for rigid (single) templates and expanded through the development of models for flexible templates. This global optimization method does not rely on random mutations and is theoretically guaranteed to search the complete sequence space and determine a global solution. This is a major advantage of our approach compared to all other existing approaches.

Single Structure Model: The original form of the sequence selection model proposed by Klepeis et al.^15,16 was further refined by Fung et al.²⁸ Its final form is given in Eq. 1.

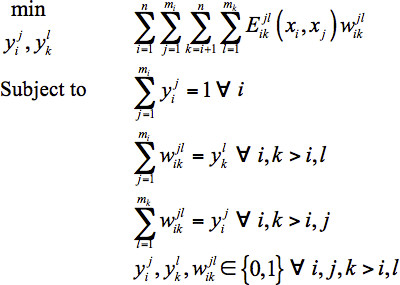
Set i=1,...,n defines the residue positions in the design template. At each position i, mutations are represented by j{i}=1,...,m_i, where m_i=20 if position i is allowed to mutate to any of the twenty natural amino acids. The alias sets k≡i and l≡j, with k>i, are employed to represent all unique pairwise interactions. Binary variables 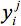and 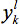are introduced to model amino acid mutations. The 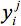variable will assume the value of one if the model assigns amino acid j to position i, and the value of zero otherwise (similarly for 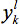). The objective function represents the sum of all pairwise energy interactions in the design template. Parameter 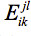which is the energy interaction between position i occupied by amino acid j and position i occupied by amino acid l , depends on the distance between the α-carbons or side chain centroids at the two positions (x_i,x_j,) as well as the type of amino acids j and l . It only contributes to the objective function if both 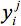and 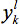are equal to one.

Fung et al.²⁸ found that formulation (1) is significantly more computationally efficient than twelve other equivalent quadratic assignment-like models for sequence selection.^28,29 In particular, it outperformed the original model proposed by Klepeis et al.^15,16 on two sequence selection problems for human beta-defensin-2: one at a complexity level of 3.4x10⁴⁵ and the other at 6.4x10³⁷ with 49 additional linear biological constraints. The original model proposed by Klepeis et al.^15,16 was found to take 53,263 central processing unit (CPU) sec and 4,578 CPU sec respectively to solve the two problems to global optimality using CPLEX 9.0³⁰ on a Pentium IV 3.2 GHz processor. Formulation (1) only took 649 CPU sec and 14 CPU sec to perform the same tasks, corresponding to an 82-fold and 327-fold improvement in computational efficiency.

Weighted Average Model: Fung et al.²⁸ developed two models to handle the typical case of de novo protein design in which the design template is flexible, containing a set of structures. The Weighted Average Model uses a weighted average energy, 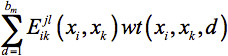, in place of the energy parameter 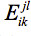(x_i,x_k) in the Single Structure Model (Eq. 1). The weights wt(x_i,x_k,d) are determined by the frequencies of the distance between x_i and x_k falling into distance bin d in the template structures. The final form of the Weighted Average Model is given in Eq. 2.

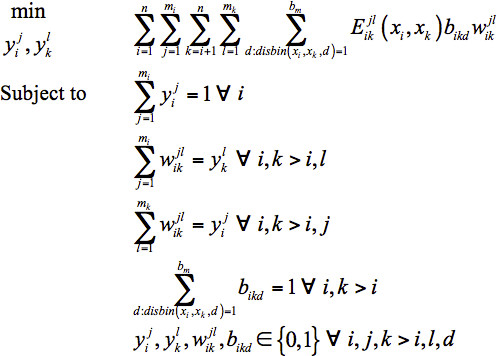
Distance Bin Model: The second sequence selection model for flexible template structures incorporates the distance information from the multiple structures by introducing a binary variable b_ikd. This variable equals one if the distance between x_i and x_k falls into distance bin d , and is zero otherwise. Another parameter introduced, disbin(x_i, x_k, d) , equals one if the distance between x_i and x_k in any of the template structures falls into distance bin d and is zero otherwise. Since only one distance bin per amino acid pair will contribute to the total energy,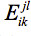 in the objective function is replaced with 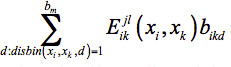. This, however, introduces nonlinearity into the objective function. Further details on linearizing the model and additional constraints that need to be added for feasibility can be found in Fung et al.²⁸ The Distance Bin Model is given in Eq. 3.

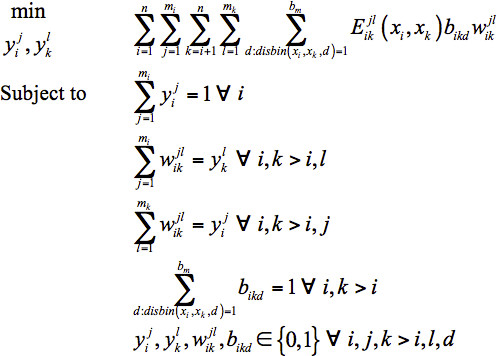
Any of the above formulated Integer Linear Programming (ILP) problems^15-17 can be solved rigorously using branch-and-bound techniques.^28-30 Such techniques guarantee consistent and reliable convergence to the global minimum energy sequence.

Stage Two: Validation: Figure 2 provides a detailed overview of the two Stage Two approaches. The figure shows the steps required to calculate the final ranking metric and the number of structures generated in each step.

Fold Specificity: Fold specificity is a metric used for ranking preliminary designs derived in Stage One. The aim of the calculation is to find how well each sequence folds into the template structure relative to the original sequence of the template, based on energy calculations. There are two approaches for how to do this, each with different computational demands.

The first approach was implemented by Klepeis et al.^15,16 This approach utilizes the protein structure prediction framework ASTRO-FOLD, ^26,27,31-47 which is based on deterministic global optimization. This approach is not currently used in the implementation of Protein WISDOM since it is very computationally demanding. Recognizing computational resource limitations and the need to perform this calculation on potentially hundreds to thousands of sequences in design, Fung et al.¹⁷ proposed a more efficient approach using TINKER/CYANA.^48-50 The approach involves defining a flexible template of the structure. The flexible template can be defined using upper and lower bounds on the distances between C^α atoms, as well as the ϕ and ψ angles of the residues. For a single structure, the initial distances and dihedral angles are used and bounds are defined either as a fixed distance or a percentage. The default bounds are ±10% for C^α distances or ±10° for dihedral angle bounds. For a flexible template, bounds can be obtained from the maximum and minimum values seen across all template structures given as input to design. Once initial bounds are defined for each sequence, ensembles containing hundreds of conformers are generated using CYANA 2.1.^48,49The conformers are generated using a torsion angle dynamics simulated annealing protocol in CYANA that heats the protein rapidly and slowly cools it, tracking the conformations sampled. After the simulated annealing, a local energy minimization is performed that minimizes the clashes from Van der Waals radii overlapping, as well as violations in the distance and angle constraints. By default, 500 final structures are generated. Each structure in the ensemble for each sequence is subjected to a local minimization in TINKER 3.6,⁵⁰ using the AMBER forcefield.⁵¹ The final potential energy of each minimized structure is tabulated. This overall approach is performed for the starting sequence as well as each candidate mutant sequence. Then, the Fold Specificity of each mutant sequence to the target fold can be calculated relative to the native sequence using the following Boltzmann distribution (Eq. 4).

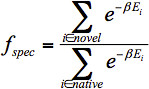
Approximate Binding Affinity: The approximate binding affinity calculation method is used to rank the designed sequences that are in complex with a target protein. These calculations can be done on the sequences directly from Stage One or can be performed on the high fold specificity sequences obtained from the fold specificity step.

Lilien et al.⁵² proposed an approach for the calculation of approximate binding affinities of protein-ligand complexes. It is based on generating rotamerically-based ensembles of the protein, the ligand, and the protein-ligand complex and using those ensembles to calculate partition functions. This approximate binding affinity is denoted as K* and is defined by Eq. 5.

Here q_PL is the partition function of the protein-ligand complex, q_b is the partition function of the free protein, and q_L is the partition function of the free ligand. The partition functions are defined in Eq. 6, where the sets B, F and L contain the rotamerically-based conformations of the bound protein-ligand complex, the free protein, and the free ligand, respectively. E_n is the energy of conformation n, R is the gas constant, and T is the temperature.

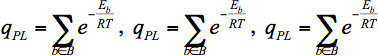
Structure Prediction: In order to begin calculating K* , a 3D structure of each sequence is needed. This is done using the Rosetta AbRelax function,^53-55 part of the Rosetta 3.4 software package. The strategy behind the AbRelax algorithm is based upon experimental observation that the local structure of the protein is influenced but not uniquely determined by the local sequence of the protein. A Monte Carlo algorithm is used to replace local protein structures with sequence derived structural fragments. This method produces the final compact protein structures that account for non-local interactions such as buried hydrophobic residues, paired β strands, and specific side chain interactions.

Clustering: The structures from AbRelax are then clustered based upon their φ and ψ angles using OREO.^56,57 This clustering method elucidates representative backbone structures of the entire structural ensemble. The average structures from the ten largest clusters and the overall lowest energy structure are chosen for docking to the target protein. This provides 11 unique backbone structures for each peptide sequence, incorporating backbone flexibility into the ensemble generation.

Docking Prediction: Docking prediction is done using RosettaDock.^58-60 For each sequence, each of the 11 peptide backbone structures is docked against the target protein. In this case, since the binding site is known, the peptides are placed near the binding site and allowed to translate 3 Å normal to the binding site, 8 Å parallel to the binding site, and rotate 8°. RosettaDock uses a Monte Carlo algorithm for low and high resolution docking movements. Each docking run generates a large ensemble of complex structures. The ten lowest energy complexes in each of the 11 runs are used as starting structures in the final rotamerically-based conformation ensemble generation (110 starting structures per sequence).

Final Ensemble Generation: RosettaDesign⁶¹ is used to generate the final rotamerically-based conformation ensemble because it can be used to generate a number of structures by only adjusting the rotamers on the side chains through the fixbb function. RosettaDesign is given a number of starting structures, and for each structure, a residue is randomly chosen and the rotamer changed through a Monte Carlo algorithm. This is repeated until thousands of rotamer substitutions are attempted and gives a final low-energy conformation that will contribute highly to the partition function.

To generate the peptide ensemble, the ten lowest-energy peptide structures from each of the ten largest clusters plus the ten overall lowest-energy peptide structures are used as starting structures for RosettaDesign (110 total starting structures). For each starting structure, 200 rotamer conformers are generated, giving a final ensemble of 22,000 structures (set L in Eq. 6). The ensemble incorporates both backbone flexibility and rotamer flexibility.

The complex ensemble is generated similarly by taking the 110 starting structures from the docking prediction step and generating 200 rotamer conformers per starting structure. The final ensemble size is 22,000 structures (set B in Eq. 6). Flexibility is taken into account by the various peptide backbone structures used, the various docked conformations, and the rotamer conformers for each starting structure.

The protein ensemble is generated by running RosettaDesign on just the target protein structure. In this case, 2,000 rotamer conformations are generated for the single starting structure, so the final ensemble size is 2,000 structures (set F in Eq. 6).

Protein WISDOM

Protein WISDOM, which stands for Protein Workbench for In Silico De novo design Of bioMolecules, is an online tool that gives the academic community access to our de novo protein design framework in a user-friendly way. It can handle several commonly encountered design objectives, from designing single protein chains to adopt a template fold to designing novel peptides that will bind to a target protein. The next two sections describe the capabilities of Protein WISDOM with regards to the two main types of protein design problems encountered. The first type applies sequence selection to select novel sequences that are favorable in the given design template and then uses fold specificity to validate the novel sequences. The second type uses sequence selection to select novel sequences of a peptide bound in a complex and then uses both fold specificity and approximate binding affinity calculations to validate the novel sequences.

User Registration

Visit the Protein WISDOM web page at http://www.proteinwisdom.org.

Click the User Login button on the top right of the page. Click the "Click here" to register.

Fill out information related to email address and requested username and click continue.

Fill out additional information on name, institution, group, address. Click the checkbox to agree to terms of use. Click the "Submit Registration" button.

Stage One: Sequence Selection

Submission of Protein Sequence and Template Structure(s)

Click on the User Login button to begin the protein design experiment. The user is presented with their "User Homepage" (Figure 3) which lists the number of jobs they have submitted, the number of structures (templates) they have uploaded, and a list of the structures they have uploaded so far.

Start a new design job by clicking "Create New Job." The user is taken to the "Job Submission" page (Figure 4). Give the job a name, and indicate if it is based on a previous job (i.e. the same design template, mutation sets, and biological constrains can be imported into a new job, however the user will have the ability to modify the mutation sets and biological constraints). Click "continue."

Upload the protein structure(s) of the design template (Figure 5). This template must be in standard protein data bank (PDB) format. It can be a rigid template (one set of coordinates for every atom) or a flexible template (multiple models, such as obtained from NMR solution structures). For the case of designing a single protein, there can only be one chain in the template. A user can upload a new template or select from existing templates they have previously uploaded. Optionally indicate the pdb ID of the template, if available. If multiple templates are uploaded, be sure each model begins with "MODEL #" and ends with "ENDMDL." Ensure every residue is designated by a natural amino acid. Click "Continue."

Upon successful upload of the template, Protein WISDOM will display the number of residues, chains, and models it found in the template, list the sequence, and ask the user to verify the template. Confirm the template structure if it has been correctly inputted, and click "Continue."

Once the template has been successfully uploaded and confirmed, the user is taken to the "Main Control Page" (Figure 6). On this page, the user can view the job status, modify the mutation sets and biological constraints, and submit the job for Stage One: Sequence Selection. At this point, since Stage One has not completed, there are no options for Stage Two. Those appear once results from Stage One are available.

Selection of Mutation Sets

Click on the "Mutation Sets" link on the "Main Control Page" to define mutation sets.

Select which residues will be allowed to mutate, and select which amino acids they are allowed to mutate to (Figure 7). By default, the allowable amino acids at any given position are selected based upon Solvent Accessible Surface Area (SASA). Mutation sets are required.

Click "Save Changes" after mutation sets are selected. The user can choose to continue editing the mutation set. When finished editing the mutation set, click to return back to the "Main Control Page."

Selection of Biological Constraints

Click on the "Biological Constraints" link on the "Main Control Page" to define biological constraints.

Specify charge or amino acid content constraints across the whole protein or a portion of the protein (Figure 8).

Limit the total number of mutations allowed to occur, if required. Biological constraints are optional. Click to return to the "Main Control Page" when finished.

Submission of Stage One: Sequence Selection

Click on the "Begin Stage 1" link to bring user to "Submit Stage 1" page.

Select the chain to design (Figure 9), the number of sequences to generate, the distance-dependent forcefield, and the model. If a complex is being design and a Fold Specificity calculation is desired, one must choose only a single chain to design. If the uploaded template was a single structure, or a "rigid template," only the Single Structure model is allowed. If the uploaded template is flexible, the user has the option to select from all three models: Single Structure, Weighted Average, and Distance Bin. Take note of the computational complexity of the optimization to be solved. There is an upper limit of 20²⁵ for computational complexity allowed.

Submit the job. The user is redirected back to the "Main Control Page" (Figure 10). The Job Status will be updated to indicate the current progress of the job. The job will become locked for editing after submission.

Upon completion of the job, the user receives an email with the results, which consist of a list of designed sequences. The results are also viewable on the "Main Control Page." A box for Stage 2: Fold Specificity appears on the page to enable the user to perform this validation.

Stage Two: Fold Specificity Calculations

Fold Specificity Submission

Click "Begin Stage 2: Fold Specificity" to enter the "Build Stage 2" page. Define the upper and lower C^α-C^α distance bounds by specifying the Template flexibility factor either as a percentage of distance, or as a fixed distance. Define upper and lower angle bounds on the φ and ψ dihedral angles by specifying the Template flexibility factor as a percentage. Note that when using a flexible template, the upper and lower distance bounds are taken as the lowest and highest distance values across all the template models. Likewise, upper and lower angle bounds are taken from the highest and lowest angle values across all the models.

Click the "Submit" button.

Specify the number of structures per sequence to generate and click "Continue." Note there is an upper bound of 500 structures per sequence to generate.

Click "Continue" to confirm intent to submit for fold validation. Stage One and Stage Two are locked for editing until the completion of Stage Two.

Upon completion of the job, an email is sent to the user with the results. View the results on Protein WISDOM on the "Main Control Page" (Figure 11). Here the text files containing designed sequences, corresponding energy values from Stage One and fold specificity values from Stage Two can be viewed and downloaded. In addition, the user may click the "View Results" link which displays a table in the browser with Stage One ranks and energy values as well as Stage Two ranks and fold specificity values.

Stage Three: Approximate Binding Affinity Calculations for Protein-peptide Complexes

Approximate Binding Affinity calculations calculate the affinity of the designed ligand protein/peptide to the rest of the complex. These calculations can be performed directly after Stage One, or after Fold Specificity calculations have been completed.

Click on "Sequence #" to select the sequence to begin approximate binding affinity calculation. User will be directed to the "Select Sequence" page, which presents a list of the designed sequences along with their sequence selection and fold specificity ranks. Only one sequence can be selected at a time for approximate binding affinity calculation, as the calculations are very computationally demanding. Upon completion of a sequence, the user may select another sequence to have the approximate binding affinity calculated, and this result is added to the previous result, displaying the approximate binding affinity for all completed sequences. Once a sequence is selected and saved, the user is redirected to the "Main Control Page."

Click "Begin Stage 2: Approximate Binding Affinity" to submit the job. Upon completion, results are emailed to the user, which include an attachment containing the sequence number, approximate binding affinity, and values of the partition functions in Eq. 6. For every subsequent approximate binding affinity job, this file contains the results for all the completed sequences. Full results (from sequence selection, fold specificity, and approximate binding affinity) can also be viewed by accessing the "Main Control Page" for the job (Figure 12).

Результаты

De Novo Design of Entry Inhibitors for HIV-1

The de novo design framework implemented in Protein WISDOM has been used for the design of inhibitor peptides for several important therapeutic systems (Tables 1 and 2). One system of note is the design of peptides to inhibit HIV-1 entry to the host cell receptor CD4, which is here used as a representative system to demonstrate the practical use of the Protein WISDOM interface. The peptides were designed to target the...

Обсуждение

The de novo protein design framework consists of two stages, a sequence selection stage and a validation stage. The framework is robust enough to handle rigid and flexible design templates, and can be applied to single protein design or complex protein design. The framework has been successfully applied to numerous protein systems with applications to dozens of diseases. A number of the designs have been experimentally validated, providing the most potent inhibitors or agonists of some proteins discovered to dat...