Rate laws describe the relationship between the rate of a chemical reaction and the concentration of its reactants. In a rate law, the rate constant k and the reaction orders are determined experimentally by observing how the rate of reaction changes as the concentrations of the reactants are changed. A common experimental approach to the determination of rate laws is the method of initial rates. This method involves measuring reaction rates for multiple experimental trials carried out using different initial reactant concentrations. Comparing the measured rates for these trials permits determination of the reaction orders and, subsequently, the rate constant, which together are used to formulate a rate law.

The rate of a reaction, for example, involving nitric oxide with ozone [NO (g) + O₃ (g) ⟶ NO₂ (g) + O₂ (g)] can be determined from the experimental data of method of initial rates, in the laboratory.

Trial	[NO] (mol/L)	[O3] (mol/L)	Δ[NO2]/Δt (mol/L·s)
1	1.00 × 10−6	3.00 × 10−6	6.60 × 10−5
2	1.00 × 10−6	6.00 × 10−6	1.32 × 10−4
3	1.00 × 10−6	9.00 × 10−6	1.98 × 10−4
4	2.00 × 10−6	9.00 × 10−6	3.96 × 10−4
5	3.00 × 10−6	9.00 × 10−6	5.94 × 10−4

From the rate data, a generic rate law; rate = k[NO]^m[O₃]ⁿ is formulated. The values of the reaction orders m and n, and rate constant k are determined from the experimental data using a three-part process:

In step 1, the value of m is determined from the data in which [NO] varies, and [O₃] is constant. In trials 3, 4 and 5, [NO] varies while [O₃] remains constant. When [NO] doubles from trial 3 to 4, the rate doubles, and when [NO] triples from trial 3 to 5, the rate also triples. Thus, the rate is also directly proportional to [NO], and m in the rate law is equal to 1.

In step 2, the value of n is determined from data in which [O₃] varies, and [NO] is constant. In trials 1,2 and 3, [NO] is constant and [O₃] varies. The reaction rate changes in direct proportion to the change in [O₃]. When [O₃] doubles from trial 1 to 2, the rate doubles; when [O₃] triples from trial 1 to 3, the rate increases also triples. Thus, the rate is directly proportional to [O₃], and n is equal to 1. The rate law is thus: rate = k [NO]¹ [O₃]¹ = k [NO][O₃]

In step 3, the value of k is determined from one set of concentrations (for instance, the data from trial 1) and its corresponding rate.

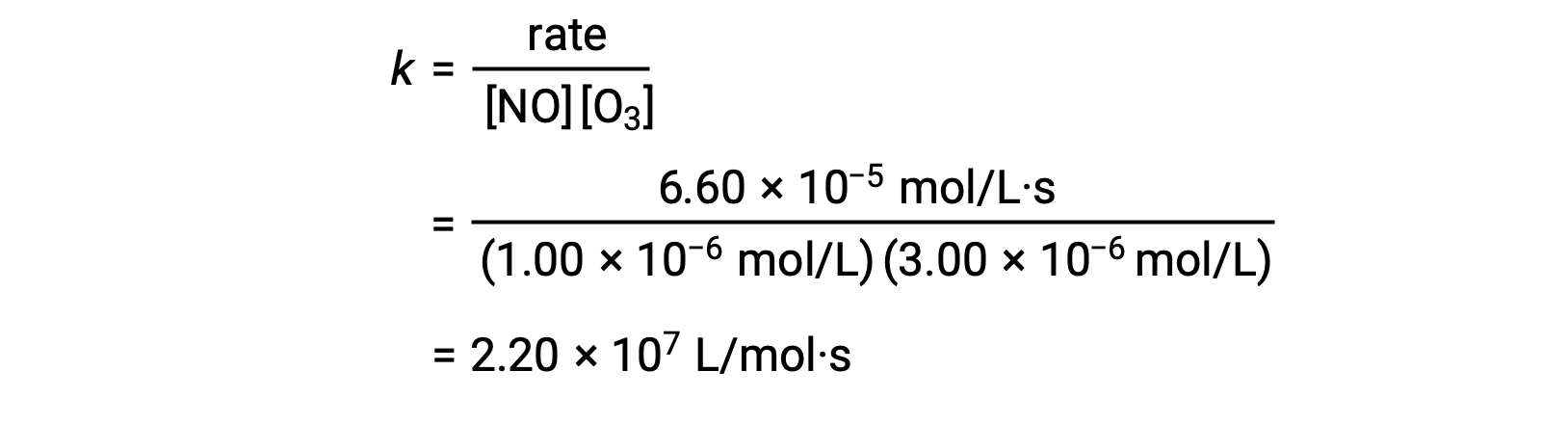
In reactions where the data from the method of initial rates does not directly imply the relation between initial concentrations and initial rates, a calculation involving the ratio of rate laws can be employed to calculate the reaction order and rate constant.

For example, the general rate law for the reaction 2 NO (g) + Cl₂ (g) ⟶ 2 NOCl (g) is expressed as: rate = k [NO]^m [Cl₂]ⁿ.

The data from the method of initial rates are:

Trial	[NO] (mol/L)	[Cl2] (mol/L)	Initial Rate (mol/L·s)
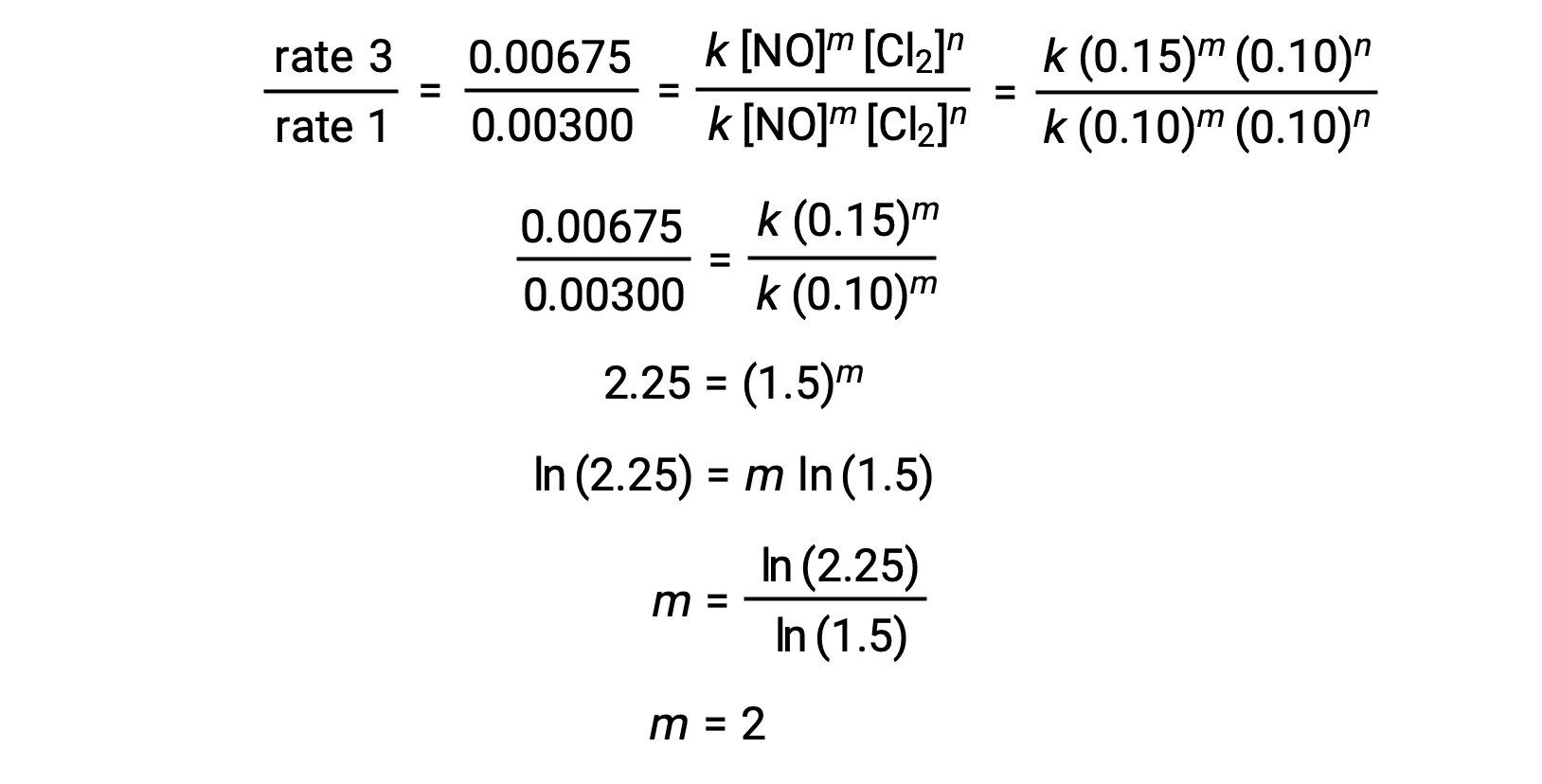
1	0.10	0.10	0.00300
2	0.10	0.15	0.00450
3	0.15	0.10	0.00675

The values of m and n can be determined from the experimental data using an algebraic approach, following which the value of k is determined.

In step 1, the value of m is determined from the data in which [NO] varies and [Cl₂] is constant. A ratio of rate laws is expressed by substituting data from two different trials (for instance trial 3 and trial 1).

In step 2, the value of n is determined from data in which [Cl₂] varies, and [NO] is constant.

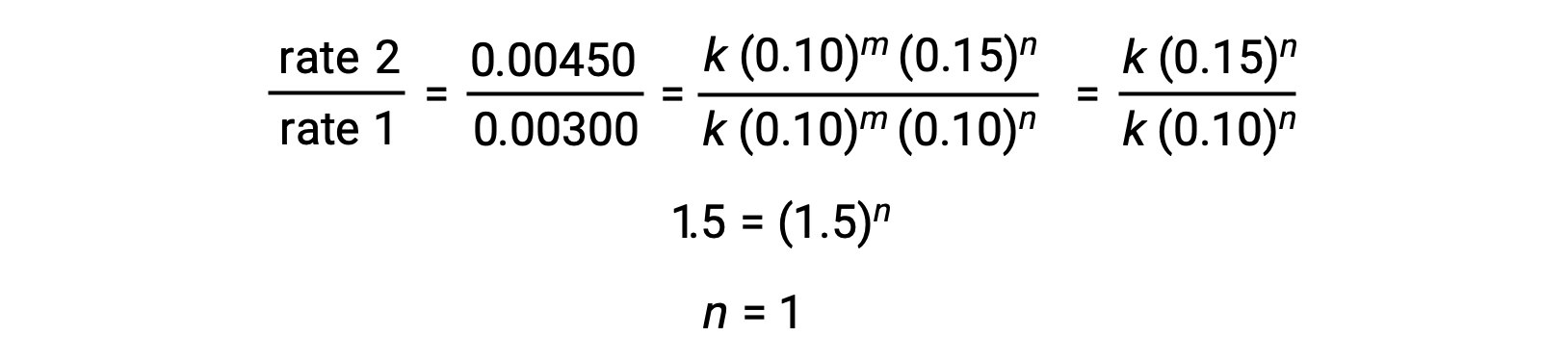
Using the computed values of m and n the rate law is expressed as rate = k [NO]² [Cl₂].

In step 3, the numerical value of the rate constant k is determined with appropriate units. The units for the rate of a reaction are mol/L·s. The units for k is concluded by substituting the units of all other parameters in the rate law. In this example, the concentration units are mol³/L³. The units for k should be L²/mol²·s so that the rate is in terms of mol/L·s. The value of k is determined once the rate law expression has been solved, by simply substituting the values from any of the experimental trials (for instance trial 1).

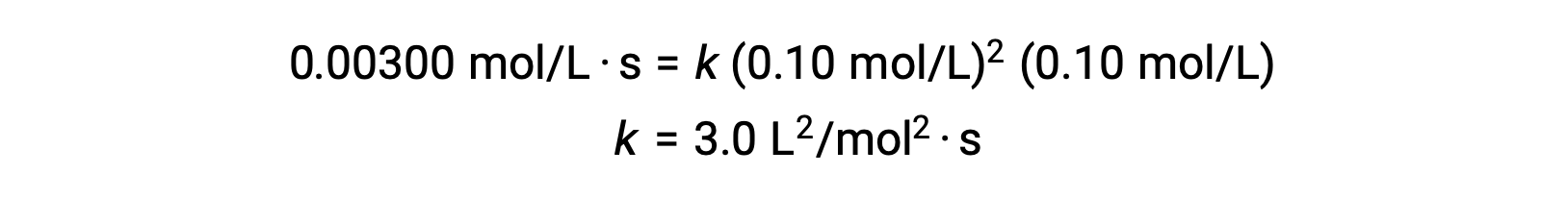
Reaction Order and Rate Constant Units

In some reactions, the reaction orders in the rate law happen to be the same as the coefficients in the chemical equation for the reaction. This is merely a coincidence and very often not the case. Rate laws may exhibit fractional orders for some reactants, and negative reaction orders are sometimes observed when an increase in the concentration of one reactant causes a decrease in reaction rate. Rate laws are determined by experiment only and are not reliably predicted by reaction stoichiometry.

The units for a rate constant will vary as appropriate to accommodate the overall order of the reaction. The unit of the rate constant for a zero-order reaction is mol/L·s (or M/s) and that for a first-order reaction is 1/s. The unit of the rate constant for a second-order reaction is L/mol·s (or 1/M·s) and that for a third-order reaction is L²/mol²·s. Although the specific units for concentration and time are indicated as (mol/L) and (s), any other valid units can be used to represent the properties of concentration and time.

This text is adapted from Openstax, Chemistry 2e, Section 12.3: Rate Laws.