10.13 : Vector Transformation in Rotating Coordinate Systems
Consider a vector rotating about an axis with an angular velocity, such that its tip sweeps a circular path.
In time Δt, the vector moves through an angle given by the product of the angular velocity and time. So, the tip of the vector moves by a magnitude ΔB.
Here, α is the angle between the vector and the angular velocity vector.
The rate of change of the vector 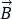 equals the cross-product of the angular velocity and the vector itself.
equals the cross-product of the angular velocity and the vector itself.
The above relation is valid for any vector that undergoes pure rotation at a constant angular velocity along a fixed rotational axis.
Now, consider an arbitrary vector in an inertial frame of reference. Its time derivative in this frame can be written considering the time derivative of its scalar components along the three coordinate axes.
When viewed from a rotating frame of reference, the scalar components and the unit vectors change. The magnitude and direction of the vector remain the same, regardless of the coordinate system chosen to assign its components.
Taking the time derivative of the vector in the rotational frame of reference gives two terms.
The first term is essentially the time derivative of the vector measured in the rotating frame of reference. The unit vectors in the rotating system rotate with a constant angular velocity. So, the time derivative of the unit vectors along the three coordinate axes is equal to the cross product of the angular velocity and the unit vectors in the rotating frame. Substituting the expression of the rate of change of unit vectors, the second term can be written as the cross product of the angular velocity and the vector.
So, the time derivative of any arbitrary vector in the inertial frame is equal to its time derivative in the rotating frame plus the cross product of the angular velocity and the vector.
When the arbitrary vector is replaced with a position vector, the transformation equation for the velocity vector is obtained. The velocity vector in the inertial frame equals the velocity vector in the rotational frame plus the cross product of angular velocity and the position vector.
Similarly, replacing the arbitrary vector with a velocity vector yields the transformation equation for the acceleration vector.
From Chapter 10:

Now Playing
10.13 : Vector Transformation in Rotating Coordinate Systems
Rotation and Rigid Bodies
1.5K Views

10.1 : Angular Velocity and Displacement
Rotation and Rigid Bodies
15.1K Views

10.2 : Angular Velocity and Acceleration
Rotation and Rigid Bodies
9.1K Views

10.3 : Rotation with Constant Angular Acceleration - I
Rotation and Rigid Bodies
6.7K Views

10.4 : Rotation with Constant Angular Acceleration - II
Rotation and Rigid Bodies
5.9K Views

10.5 : Relating Angular And Linear Quantities - I
Rotation and Rigid Bodies
6.5K Views

10.6 : Relating Angular And Linear Quantities - II
Rotation and Rigid Bodies
5.4K Views

10.7 : Moment of Inertia
Rotation and Rigid Bodies
12.0K Views

10.8 : Moment of Inertia and Rotational Kinetic Energy
Rotation and Rigid Bodies
7.3K Views

10.9 : Moment of Inertia: Calculations
Rotation and Rigid Bodies
6.7K Views

10.10 : Moment of Inertia of Compound Objects
Rotation and Rigid Bodies
6.1K Views

10.11 : Parallel-axis Theorem
Rotation and Rigid Bodies
6.5K Views

10.12 : Perpendicular-Axis Theorem
Rotation and Rigid Bodies
2.7K Views

10.14 : Coriolis Force
Rotation and Rigid Bodies
3.1K Views
Copyright © 2025 MyJoVE Corporation. All rights reserved