Electric Potential
Source: Yong P. Chen, PhD, Department of Physics & Astronomy, College of Science, Purdue University, West Lafayette, IN
Electric potential, also known as "voltage", measures the electric potential energy per unit charge. Electric field is a scalar quantity and is fundamental to many electrical effects. Like potential energy, what is physically meaningful is the difference in the electric potential. For example, the spatial variation in the electric potential is related to the electric field, which gives rise to the electric force on a charge. The difference in the electric potential between two points in a resistor drives the electric current flow.
This experiment will use both a volt meter and a fluorescent tube to demonstrate the electric potential (more accurately, the potential difference between two points in space) generated by a charged sphere. The experiment will demonstrate the concept of equipotential surfaces, which are perpendicular to the electric fields.
A point charge Q located at the origin (r = 0) produces an electric potential:
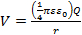 (Equation 1)
(Equation 1)
at any point in the space with a distance r from the charge (at origin r = 0). Equation 1 also describes the electric potential produced by a uniformly charged sphere (centered at r = 0) with total charge Q in the space outside the sphere (Figure 1). In both cases, the "reference" point (where the potential is zero) is at the infinite distance away from the charge. The electric potential varies along the radial direction, which is the direction of the electric field.
For two points P1 and P2 with distance r1 and r2 away from the origin (center of the charge), respectively, the potential difference between these two points is:
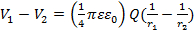 (Equation 2)
(Equation 2)
If point P2 is at infinity (→∞), this reduces Equation 2 to Equation 1. Therefore, there is a potential difference between two points if and only if these two points have a different distance away from the origin (center of the charge). A spherical surface centered at the origin is an "equipotential surface" in this case. Note in this case, the electric field (along the radial direction) is perpendicular to the equipotential surface (sphere). This turns out to be generally true: the equipotential surface is perpendicular to the direction of electric field.

Figure 1: Diagram showing a charged sphere connected to an electric generator. A voltmeter is used to measure the electric potential at a point "A" (with distance r from the center of the sphere).
1. Electric Potential Due to a Charged Sphere
- Obtain a van der Graff generator, which can put charge on a metal sphere. The center of the sphere is defined as the origin for this experiment.
- Obtain a voltmeter. Connect (using conducting cables) its "−" terminal to the ground or reference terminal on the van der Graff generator, or to an electrical ground (such as a large conducting pipe) far away (at least several meters) from the generator. Connect its "+" terminal to a voltmeter cable with a voltage probe tip that can be moved around. The schematic connection is shown in Figure 1.
- Turn the crank of the generator by at least 10 turns to charge the sphere.
- With the voltmeter turned on, place the tip of the voltage probe (connected to the "+" terminal of the voltmeter) about 0.5 m away from the origin. Use a ruler to measure or mark the distance beforehand, if desired. Record the voltage reading on the voltmeter. Move the tip around but maintain the distance away from the origin. Observe the voltmeter reading.
- Repeat the above step with the voltage probe tip placed at about 1 m and 1.5 m, respectively.
- Obtain a (hand held) fluorescence tube. Bring the tube to about 0.5 m away from the center of the charged sphere ( Figure 2a). First, orient the tube so that it is along the radial direction away from the sphere. Observe the tube (turn off the lights to ease the observation in relative darkness). Then rotate the tube by 90 degrees so that it is perpendicular to the radial direction ( Figure 2b). Observe the tube again.
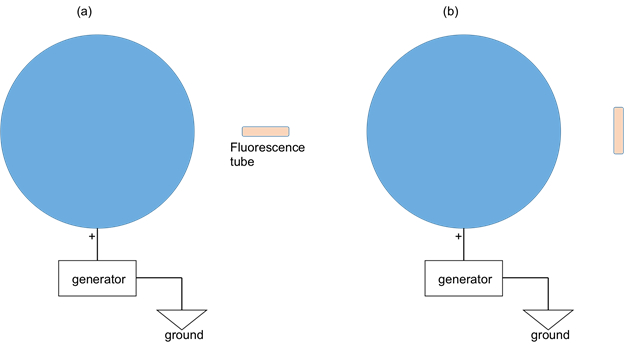
Figure 2: Diagram showing a charged sphere connected to an electric generator. A fluorescence tube is used to indicate the potential difference between the two ends of the tube. In the case of ( a) the tube is oriented along the radial direction; and ( b) the tube is oriented perpendicular to the radial direction.
In steps 1.4-1.5, the voltmeter can be observed to give similar readings if the probe tip is kept at similar distances from the origin (that is, on an equipotential surface). However, the voltage drops if the probe moves farther away from the origin. The voltage reading at 1 m and 1.5 m away will be about 1/2 and 1/3 of the reading at 0.5 m away, respectively. If the voltage V measured versus the inverse distance (1/r) is plotted, a straight line results, as expected from Equation 1.
Electric potential (voltage) is ubiquitous and perhaps the most commonly used quantity in electricity. It is often much more convenient to use electric potential (which is a scalar) than electric field (which is a vector), even though the two can be related to each other. Electric potential difference is used to drive and control charge motion (accelerate/decelerate/deflect charges), for example in a TV screen or electron microscope. Electric potential difference (what we usually call voltage) is also what drives current flow in a conductor. Whenever one measures a voltage, one is measuring the electric potential difference between two points (one of which is sometimes a reference point or ground defined to have zero potential).
The author of the experiment acknowledges the assistance of Gary Hudson for material preparation and Chuanhsun Li for demonstrating the steps in the video.
Skip to...
Videos from this collection:

Now Playing
Electric Potential
Physics II
103.7K Views

Electric Fields
Physics II
77.2K Views

Magnetic Fields
Physics II
33.2K Views

Electric Charge in a Magnetic Field
Physics II
33.6K Views

Investigation Ohm's Law for Ohmic and Nonohmic Conductors
Physics II
26.1K Views

Series and Parallel Resistors
Physics II
33.0K Views

Capacitance
Physics II
43.6K Views

Inductance
Physics II
21.4K Views

RC/RL/LC Circuits
Physics II
142.4K Views

Semiconductors
Physics II
29.5K Views

Photoelectric Effect
Physics II
32.4K Views

Reflection and Refraction
Physics II
35.6K Views

Interference and Diffraction
Physics II
90.6K Views

Standing Waves
Physics II
49.5K Views

Sound Waves and Doppler Shift
Physics II
23.3K Views
Copyright © 2025 MyJoVE Corporation. All rights reserved