Method Article
High-resolution, High-speed, Three-dimensional Video Imaging with Digital Fringe Projection Techniques
In This Article
Summary
This video describes the fundamentals of digital fringe projection techniques, which provide dense 3D measurements of dynamically changing surfaces. It also demonstrates the design and operation of a high-speed binary defocusing system based on these techniques.
Abstract
Digital fringe projection (DFP) techniques provide dense 3D measurements of dynamically changing surfaces. Like the human eyes and brain, DFP uses triangulation between matching points in two views of the same scene at different angles to compute depth. However, unlike a stereo-based method, DFP uses a digital video projector to replace one of the cameras1. The projector rapidly projects a known sinusoidal pattern onto the subject, and the surface of the subject distorts these patterns in the camera’s field of view. Three distorted patterns (fringe images) from the camera can be used to compute the depth using triangulation.
Unlike other 3D measurement methods, DFP techniques lead to systems that tend to be faster, lower in equipment cost, more flexible, and easier to develop. DFP systems can also achieve the same measurement resolution as the camera. For this reason, DFP and other digital structured light techniques have recently been the focus of intense research (as summarized in1-5). Taking advantage of DFP, the graphics processing unit, and optimized algorithms, we have developed a system capable of 30 Hz 3D video data acquisition, reconstruction, and display for over 300,000 measurement points per frame6,7. Binary defocusing DFP methods can achieve even greater speeds8.
Diverse applications can benefit from DFP techniques. Our collaborators have used our systems for facial function analysis9, facial animation10, cardiac mechanics studies11, and fluid surface measurements, but many other potential applications exist. This video will teach the fundamentals of DFP techniques and illustrate the design and operation of a binary defocusing DFP system.
Introduction
Digital fringe projection (DFP) techniques are based upon correlation and triangulation between two views of the same scene at different angles, the same principle employed by the human eyes and brain to achieve stereo vision. However, unlike a stereo-based method, DFP uses a digital video projector to replace one of the cameras1. The projector rapidly projects a known sinusoidal pattern onto the object that the object’s surface distorts in the camera’s view. Three such distorted patterns (fringe images) at differing phase shifts from each other can be analyzed to retrieve the depth via triangulation. The use of a known pattern eliminates the difficult computational problem of identifying correspondence points, allowing the capture of depth measurements at the camera resolution. For example, with a 576 x 576 camera, the technique can capture 331,776 points. This allows DFP systems to measure very fine details such as the movement of facial muscles in human emotions.
3D optical imaging techniques for static or quasi-static events have been extensively studied over the past few decades and have seen great success in video game design, animation, movies, music videos, virtual reality, telesurgery, and many engineering disciplines5. Though numerous 3D profilometry techniques exist, they can be classified into two categories: surface contact methods and surface noncontact methods. Both the coordinate measurement machine (CMM) and the atomic force microscope (AFM) require contact with the measuring surface to obtain 3D profiles at high accuracy. This requirement places severe restrictions on the speed of contact methods. They cannot reach kHz measurement speed with thousands of points per scan.
Surface noncontact techniques typically utilize optical triangulation methods (e.g. stereo vision, spacetime stereo, structured light). By actively projecting known patterns onto the objects, structured light techniques can be used to measure surfaces without strong local texture variations1. Fringe analysis is a special group of structured light techniques that uses sinusoidal structured patterns (also known as fringe patterns). Because these patterns have intensities that vary continuously from point to point in a known manner, they boost the structured light techniques from projector-pixel resolution to camera-pixel resolution12. In the recent past, fringe analysis techniques were instrumental in achieving high-resolution 3D imaging.
The digital fringe projection (DFP) technique uses digital video projectors to generate sinusoidal fringe patterns. This technique has the merits of lower cost, higher speed, and simplicity of development, and it has been a very active research area within the past decade. Recent developments in DFP and similar digital structured light techniques are summarized in1-5. To achieve high-speed applications, a digital-light-processing (DLP) projector is preferable due to its fundamental operation mechanism. The speed and flexibility of this technique has allowed us to acquire 3D video at 40 Hz 13 and then later at 60 Hz 6,7.
Nevertheless, a fundamental speed limit exists for the traditional DFP technique. A DLP projector can only swap 8-bit color images at its maximum refresh rate (typically 120 Hz). Since the traditional fringe patterns are 8-bit grayscale images, we can encode three of them into one color image as the red, green, and blue color channels. The projector will swap each channel (and therefore each fringe pattern) at three times the refresh rate (typically 360 Hz). However, since each 3D video frame requires three fringe patterns, the maximum rate of 3D video capture is still only the refresh rate (120 Hz)3,14. To break past this hardware limitation, we have invented a modified DFP technique that uses binary defocusing8. Instead of 8-bit grayscale fringe patterns, this technique uses computer-generated 1-bit binary structured patterns. These patterns are defocused using the projector lens to become pseudo-sinusoidal patterns for DFP. Because DLP projectors can display binary images orders-of-magnitude faster than 8-bit grayscale images, the binary defocusing technology permits tens of kilohertz 3D video imaging speed with the same resolution as the conventional DFP techniques15.
The overall goal of the following protocol is to demonstrate the basic implementation and operation of a binary defocusing three-step phase-shifting DFP system. First, the protocol will cover the selection and integration of the necessary components. Then, it will discuss the simplest, most readily accessible method of calibration for the system; more complex calibration methods are available in the literature for specific applications16,17. The protocol will then focus on the procedure for 3D video capture with the system and the process for converting the fringe images into visualized 3D measurements. Finally, we will present some representative results from our real-time and high-speed systems.
Protocol
1. System Configuration
A schematic of the system is shown in Figure 1.
- Generate the fringe patterns for projection. These can be prepared well in advance by using an image programming environment such as MATLAB, OpenCV, or QT. Construct the patterns according to the three-step phase-shifting algorithm in18. Make three images, shifted in phase offset from each other by 2π/3. For binary defocusing, use a dithering technique to generate sinusoidal patterns using only black and white pixels as described in19.
- Select the digital light processing projector. A high-speed binary defocusing system requires a faster, specialized projector such as the DLP LightCommander with ALP High Speed module. Be sure to use the binary or monochromatic setting to project the fringe images. Since the image values are purely on or off, nonlinearity adjustments are not necessary. Utilize the projector’s software program to upload the patterns for phase shifting.
- Select the camera. Choose a black-and-white CCD or CMOS camera with the correct capture rate for the system. Avoid color cameras for 3D capture since color is not needed and color cameras require nonlinearity and gamma adjustments. Keep in mind that the camera will need to capture the entire set of fringe images for each 3D video frame. High-quality sinusoidal systems require precise synchronization between the projector and the camera; for binary defocusing systems this requirement is more relaxed20.
- Determine the desired maximum (x, y) range and the distance from the projector to the object (d0). Choose a range that makes sense for the application, but be sure that the area is slightly larger than the subject to reduce any optical boundary effects. Since the light output of a projector is a frustum, this (x, y) range will drive d0. Move the projector relative to a large flat projection surface until the desired (x, y) range is found, then measure d0 with a tape measure.
- Select the camera lens with the proper focal length. Using the camera’s sensor size, find the focal length such that the field of view at the distance d0 is the same as the desired imaging range (x, y).
- Determine the separation distance between the projector and the camera. A trade-off occurs here between noise and shadowing. At a large angle between these components, triangulation between feature points is more obvious, but more features get lost in shadow from the camera’s perspective. At a small angle, triangulation becomes difficult, increasing noise in the results. Typically, 10-15° is a good compromise.
2. System Calibration
This reference plane calibration is the simplest and most readily accessible method of calibration for the system. Therefore, it is the best for getting started. More accurate calibration methods are available in the literature for specific sinusoidal16 and binary defocusing17 applications. For maximum accuracy, calibration should be performed just before data capture. After calibration, the camera and projector should not be displaced relative to each other.
- Focus/defocus the projector. Carefully defocus the projection lens until the patterns at the imaging plane resemble high-quality sinusoids. This may require an iterative process of examining the data quality (Section 4) and adjusting the lens.
- Capture fringe images of a reference plane. Place a flat white board at the focal plane of the projector and in the field of view of the camera. A 3/16 in (5 mm) thick white foam core board works well, provided that the surface facing the system is not shiny or significantly blemished or torn. Record and save fringe images of this board for the data processing step.
- Capture fringe images of a reference object of known dimensions. For this step, a rigid foam cube is one simple example. Cover the cube with squares of 1/16 in (1.5 mm) white adhesive foam to make it diffuse. Place it at the focal plane of the camera in the camera’s field of view and record fringe images for the processing step.
3. Data Acquisition
- Place the object or invite the subject to sit at the focal plane of the camera. For a human subject, warn him or her that the projector light may be bright. A black cloth backdrop can be used behind the subject to hide extraneous surroundings.
- Adjust the camera aperture to optimize the light level. Sample fringe images should be as bright as possible, but not saturated. Dark images will have too much noise, while saturated areas (significant regions of maximum brightness) in images will result in the loss of details in the saturated region.
- Capture the desired number of frames. Be sure to bring a hard drive large enough to hold all of the captured images for both the subject and the calibration datasets. With the .OBJ file format, a 3D video recorded at 30 Hz for 1 min at a resolution of 640 x 480 could be over 50 GB.
4. Data Analysis and Visualization
With software optimized for speed such as our in-house GUI, this step can take place during data capture. Real-time processing allows the user to immediately detect if the resulting data is desirable for the application and adjust if necessary. However, post processing can be more flexible and higher in accuracy. Post processing is also much simpler to implement and the best place to begin.
- Compute the wrapped phase for both the calibration and subject data. In the three-step phase-shifting algorithm in18, phase describes the position of a point within the cosine function. Since we have three equations and three unknowns, we can solve the equations used to generate the fringe images in step 1.1 for the phase at each point. Because of the arctangent function, the computed phase is in the range (-π, π]; hence it is called “wrapped phase.” To improve the processing speed, we developed a fast phase wrapping algorithm that is discussed in21.
- Unwrap the phase maps. Adopt a phase-unwrapping algorithm that detects the 2π jumps in the phase and removes them by adding or subtracting multiples of 2π. We have used the fast algorithm in22 in previous systems to unwrap the phase robustly yet quickly. In the video, we demonstrate the multifrequency technique described in15, which uses additional sets of three phase-shifted patterns at differing frequencies. The wrapped phase maps from each set of three can be combined to robustly yield a single unwrapped phase map. This technique increases the depth range for accurate capture with binary defocusing.
- Optional: Compute the 2D texture. Averaging sets of three neighboring fringe images will wash out the fringe stripes and generate the 2D texture map. This can be mapped onto the 3D data during visualization if desired.
- Convert the unwrapped phase maps into depth. As described in23, depth can be computed for the calibration cube as the difference between the calibration cube phase map and the reference plane phase map. Compare this computed depth to the known depth to compute the correct depth scaling factor c0. Then, compute the depth for the subject by subtracting the reference plane phase from the subject’s phase and multiplying the results by c0.
- Compute the x- and y-coordinates. Apply the scaling factor c0 to the calibration cube depth map. Determine the conversion factor ρ from the cube dimensions in pixels to the known cube dimensions in the xy plane. Multiply the pixel count in the subject data by ρ to compute the x and y coordinates.
- Visualize the data. Individual frames can be saved in our in-house format and viewed with simple MATLAB code or saved in .OBJ format and viewed with a commercial 3D modeling program such as Blender. Due to the large amount of data in each frame, these applications may be sluggish on some computers. For more responsiveness or for live video display, write software using a computer graphics library such as OpenGL or Direct3D. This software can take advantage of the graphics processing unit (GPU) to rapidly generate the x, y, and z coordinates from the unwrapped phase, form a triangle mesh, compute lighting normals, and display the results. Using the GPU, we have achieved up to 30 Hz live 3D data visualization with approximately 300,000 points per frame.
Results
Figure 1 shows the schematic of the system. The high-speed binary defocusing system in this video consists of a Logic PD DLP LightCommander projector and a Phantom v9.1 CMOS camera.
Figure 2 presents a single frame from our 3D real-time system of a human face. This system uses a 640 x 480 camera. Thanks to the aforementioned known sinusoidal pattern, we can capture 640 x 480 = 307,200 measurements, enough resolution to record very fine details.
Figure 3 shows an example of measuring human facial expressions in 3D at 60 Hz. Here, four frames selected from a video sequence clearly demonstrate the capability of the real-time system to capture dynamic changes in finely detailed geometry.
Figure 4 demonstrates our live visualization software used in conjunction with our real-time binary defocusing 3D video system. The 3D captured video of the subject is displayed in real time on the computer monitor to his right. This software was written in C++ using the OpenGL library, GLSL, and QT. The computer used is a Lenovo laptop.
Figure 5 shows 3D frames from live rabbit heart measurement with our newly developed superfast binary defocusing system. This system can record 3D frames at 667 Hz with an image resolution of 576 x 576. A superfast rate is required to measure the heart surface without motion-induced artifacts. The heart measurement research is in collaboration with Prof. Igor Efimov at Washington University-St. Louis (see11 for further details); note that the rabbit was humanely killed and that the images were taken while the heart was still beating.
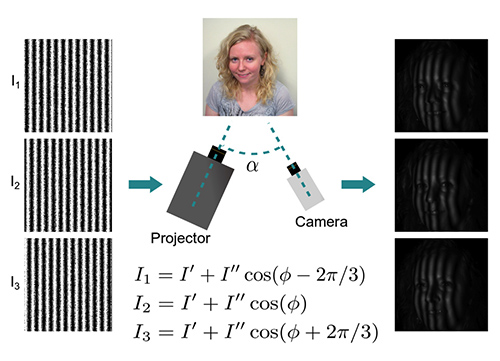
Figure 1. Layout of the 3D video imaging system. In this system, a high-speed DLP projector projects three binary dithered phase-shifted images in rapid succession onto the subject. A high-speed CMOS camera is used to capture the three fringe images one by one for computation of the depth.

Figure 2. 3D measurements of a human face at a resolution of 640 x 480, revealing fine details. Left to right shows the simultaneously captured texture perfectly aligned with the geometry, a shaded view of the geometry, the wireframe view depicting the density of the points, a close-up view of the nose area, and a close-up view of the eye region.

Figure 3. Four selected frames from 3D video of the formation of a facial expression. The video was captured at 60 Hz with a resolution of 640 x 480. These frames highlight the geometric changes in the woman’s face as she moves from a neutral expression to a smile.

Figure 4. Live 3D video capturing, processing, and rendering. The 3D measurements are displayed in real time on the computer screen to the subject’s right.
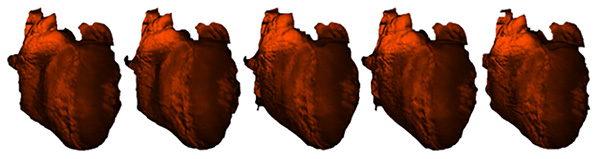
Figure 5. Capturing a live rabbit heart with our superfast 3D video imaging system. The heart is beating at approximately 200 beats/min. The 3D capture rate was 166 Hz with an image resolution of 576 x 576. See11 for further details.
Discussion
This high-resolution, real-time to superfast 3D video imaging technology is a platform technology that could potentially benefit numerous and diverse scientific fields ranging from biological science to engineering practice. Biomedical applications include precision measurements of facial movements and organ surfaces. Other applications include 3D automated quality control with detection of warped surface features; 3D enhanced videoconferencing; detailed digitization of facial features for movies and videogames; dense and rapid deformation measurements for the design and analysis of structures; and fluid surface characterization. Many biological and engineering applications (e.g. beating rabbit hearts, fluid shockwaves) require the superfast imaging rates of a binary defocusing system to correctly resolve features without aliasing artifacts.
Nevertheless, many challenges remain to the widespread adoption of this technology. Conventional DFP technology requires the projector to display 8-bit grayscale sinusoidal fringe patterns. The speed of this technique is limited by the projector’s refresh rate (typically 120 Hz). This speed is sufficient for slow motion capture such as that in facial expressions. However, numerous applications exist that require faster capture rates.
Binary defocusing technology has relaxed this speed limitation, and we have successfully created a superfast 3D video imaging system. However, this system has two drawbacks. First, it requires an expensive projector such as the DLP Discovery platform and a costly high-speed video camera such as the Vision Research Phantom v9.1. Second, since it generates sinusoidal patterns via the defocusing of squared binary patterns, the binary defocusing technique has difficulty generating sinusoidal fringes of the same quality as the traditional DFP technique and a reduced depth measurement range (for further explanation, see23). Recent investigation indicates that dithered binary sinusoidal patterns can significantly alleviate the limitations on depth measurement range19. Future research will focus on overcoming the remaining issues while preserving the merits of binary defocusing.
Another challenge is compressing and storing the large amount of data generated by high-speed, high-resolution 3D video imaging systems. Uncompressed 3D videos are drastically larger than uncompressed 2D videos. For instance, for a 3D video recorded at 30 Hz for 1 min at a resolution of 640 x 480, the .OBJ file size could be over 50 GB, making it extremely difficult to store. Since little progress has been made in the 3D video compression field, we will continue to focus on this in the future.
Disclosures
The authors have no competing financial interests.
Acknowledgements
This research was an accumulated effort that began more than 10 years ago when Dr. Zhang was a graduate student at Stony Brook University. The current and previous students in our team at Iowa State University have contributed tremendously toward advancing this technology to where it is today. This work was partially sponsored by National Science Foundation under project number CMMI 1150711, and the William and Virginia Binger Foundation.
Materials
| Name | Company | Catalog Number | Comments |
No materials or equipment used. | |||
References
- Salvi, J., Fernandez, S., Pribanic, T., Llado, X. A state of the art in structured light patterns for surface profilometry. Patt. Recogn. 43, 2666-2680 (2010).
- Gorthi, S. S., Rastogi, P. Fringe projection techniques: Whither we are. Opt. Laser Eng. 48 (2), 133-140 (2010).
- Zhang, S. Recent progresses on real-time 3-D shape measurement using digital fringe projection techniques. Opt. Laser Eng. 48 (2), 149-158 (2010).
- Su, X., Zhang, Q. Dynamic 3-D shape measurement method: A review. Opt. Laser Eng. 48 (2), 191-204 (2010).
- Geng, J. Structured-light 3D surface imaging: a tutorial. Adv. Opt. Photonics. 3 (2), 128-160 (2011).
- Zhang, S., Yau, S. -. T. High-resolution, real-time 3-D absolute coordinate measurement based on a phase-shifting method. Opt. Express. 14 (7), 2644-2649 (2006).
- Zhang, S., Royer, D., Yau, S. -. T. GPU-assisted high-resolution, real-time 3-D shape measurement. Opt. Express. 14 (20), 9120-9129 (2006).
- Lei, S., Zhang, S. Flexible 3-D shape measurement using projector defocusing. Opt. Lett. 34 (20), 3080-3082 (2009).
- Mehta, R. P., Zhang, S., Hadlock, T. A. Novel 3-D video for quantification of facial movement. Otolaryngol. Head Neck Surg. 138 (4), 468-472 (2008).
- Wang, Y., et al. High resolution acquisition, learning and transfer of dynamic 3D facial expressions. Comput. Graph. Forum. 23 (3), (2004).
- Laughner, J. I., Zhang, S., Li, H., Efimov, I. R. Mapping cardiac surface mechanics with structured light imaging. Am. J. Physiol. Heart Circ. Physiol. , (2012).
- Ekstrand, L., Wang, Y., Karpinsky, N., Zhang, S. Superfast 3D profilometry with digital fringe projection and phase-shifting techniques. Handbook of 3-D machine vision: Optical metrology and imaging. , (2012).
- Zhang, S., Huang, P. S. High-resolution real-time three-dimensional shape measurement. Opt. Eng. 45 (12), 123-601 (2006).
- Li, Y., Zhao, C., Qian, Y., Wang, H., Jin, H. High-speed and dense three-dimensional surface acquisition using defocused binary patterns for spatially isolated objects. Opt. Express. 18, 21-635 (2010).
- Wang, Y., Zhang, S. Superfast multifrequency phase-shifting technique with optimal pulse width modulation. Opt. Express. 19 (6), 5143-5148 (2011).
- Zhang, S., Huang, P. S. Novel method for structured light system calibration. Opt. Eng. 45 (8), 083601 (2006).
- Merner, L., Wang, Y., Zhang, S. Accurate calibration for 3D shape measurement system using a binary defocusing technique. Opt. Laser Eng. 51 (5), 514-519 (2013).
- Malacara, D. . Optical Shop Testing. , (2007).
- Wang, Y., Zhang, S. Three-dimensional shape measurement with binary dithered patterns. Appl. Opt. 51 (27), 6631-6636 (2012).
- Ekstrand, L., Zhang, S. Autoexposure for three-dimensional shape measurement with a digital-light-processing projector. Opt. Eng. 50 (12), 123-603 (2011).
- Huang, P. S., Zhang, S. Fast three-step phase-shifting algorithm. Appl. Opt. 45 (21), 5086-5091 (2006).
- Zhang, S., Li, X., Yau, S. -. T. Multilevel quality-guided phase unwrapping algorithm for real-time 3-D shape reconstruction. Appl. Opt. 46 (1), 50-57 (2007).
- Xu, Y., Ekstrand, L., Dai, J., Zhang, S. Phase error compensation for 3-D shape measurement with projector defocusing. Appl. Opt. 50 (18), 2572-2581 (2011).
Reprints and Permissions
Request permission to reuse the text or figures of this JoVE article
Request PermissionThis article has been published
Video Coming Soon
Copyright © 2025 MyJoVE Corporation. All rights reserved