A subscription to JoVE is required to view this content. Sign in or start your free trial.
Method Article
In Situ Measurement of Vacuum Window Birefringence using 25Mg+ Fluorescence
In This Article
Summary
Presented here is a method to measure the birefringence of vacuum windows by maximizing the fluorescence counts emitted by Doppler cooled 25Mg+ ions in an ion trap. The birefringence of vacuum windows will change the polarization states of the laser, which can be compensated by changing the azimuthal angles of external wave plates.
Abstract
Accurate control of the polarization states of laser light is important in precision measurement experiments. In experiments involving the use of a vacuum environment, the stress-induced birefringence effect of the vacuum windows will affect the polarization states of laser light inside the vacuum system, and it is very difficult to measure and optimize the polarization states of the laser light in situ. The purpose of this protocol is to demonstrate how to optimize the polarization states of the laser light based on the fluorescence of ions in the vacuum system, and how to calculate the birefringence of vacuum windows based on azimuthal angles of external wave plates with Mueller matrix. The fluorescence of 25Mg+ ions induced by laser light that is resonant with the transition of |32P3/2,F = 4, mF = 4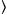 → |32S1/2,F = 3, mF = 3
→ |32S1/2,F = 3, mF = 3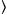 is sensitive to the polarization state of the laser light, and maximum fluorescence will be observed with pure circularly polarized light. A combination of half-wave plate (HWP) and quarter-wave plate (QWP) can achieve arbitrary phase retardation and is used for compensating the birefringence of the vacuum window. In this experiment, the polarization state of the laser light is optimized based on the fluorescence of 25Mg+ ion with a pair of HWP and QWP outside the vacuum chamber. By adjusting the azimuthal angles of the HWP and QWP to obtain maximum ion fluorescence, one can obtain a pure circularly polarized light inside the vacuum chamber. With the information on the azimuthal angles of the external HWP and QWP, the birefringence of the vacuum window can be determined.
is sensitive to the polarization state of the laser light, and maximum fluorescence will be observed with pure circularly polarized light. A combination of half-wave plate (HWP) and quarter-wave plate (QWP) can achieve arbitrary phase retardation and is used for compensating the birefringence of the vacuum window. In this experiment, the polarization state of the laser light is optimized based on the fluorescence of 25Mg+ ion with a pair of HWP and QWP outside the vacuum chamber. By adjusting the azimuthal angles of the HWP and QWP to obtain maximum ion fluorescence, one can obtain a pure circularly polarized light inside the vacuum chamber. With the information on the azimuthal angles of the external HWP and QWP, the birefringence of the vacuum window can be determined.
Introduction
In many research fields such as cold atom experiments1, measurement of the electric dipole moment2, test of parity-nonconservation3, measurement of vacuum birefringence4, optical clocks5, quantum optics experiments6, and liquid crystal study7, it is important to precisely measure and accurately control the polarization states of laser light.
In experiments involving the use of a vacuum environment, the stress-induced birefringence effect of vacuum windows will affect the polarization states of laser light. It is not feasible to put a polarization analyzer inside the vacuum chamber to directly measure the polarization states of the laser light. One solution is to use atoms or ions directly as an in situ polarization analyzer to analyze the birefringence of vacuum windows. The vector light shifts of Cs atoms8 are sensitive to the degrees of linear polarization of the incidence laser light9. But this method is time consuming and can only be applied to the linearly polarized laser light detection.
Presented is a new, quick, precise, in situ method to determine the polarization states of laser light inside the vacuum chamber based on maximizing single 25Mg+ fluorescence in an ion trap. The method is based on the relationship of the ion fluorescence to the polarization states of the laser light, which is affected by the birefringence of the vacuum window. The proposed method is used for detecting the birefringence of vacuum windows and degrees of circular polarization of laser light inside a vacuum chamber10.
The method is applicable to any atoms or ions whose fluorescence rate is sensitive to the polarization states of laser light. In addition, while the demonstration is used to prepare a pure circularly polarized light, with the knowledge of the birefringence of the vacuum window, arbitrary polarization states of laser light can be prepared inside the vacuum chamber. Therefore, the method is quite useful for a wide range of experiments.
Access restricted. Please log in or start a trial to view this content.
Protocol
1. Set up the reference directions for polarizers A and B
- Put polarizer A and polarizer B into the laser beam (280 nm fourth harmonic laser) path.
- Ensure that the laser beam is perpendicular to the surfaces of the polarizers by carefully adjusting the polarizer holders to keep the back-reflection light coincident with the incident light.
NOTE: All the following alignment procedures for the optics components must follow the same rule. The placement of polarizer A and B in the laser path is not important. The spacing between them should be large enough for the future convenient adjustment. - Put a power meter behind polarizer A and rotate the polarizer to maximize the output power. Define the azimuthal angle (see Results and Discussion) of the optical axis of polarizer A as 0°. Define the clockwise direction as the positive direction and the counterclockwise direction as the negative direction when observing along the direction of light propagation.
- Use a stepper motor rotation stage to hold polarizer A and put the power meter behind polarizer A to record the rotation angles and the output laser powers. Fit the angle vs power curve with a sinusoidal function; the maximum output power position of polarizer A is 0° azimuthal angle position.
- Put the power meter behind polarizer B and rotate polarizer B to maximize the output power. The azimuthal angle of the optical axis of polarizer B is then also 0°.
- Use another stepper motor rotation stage to hold polarizer B and put the power meter behind polarizer B to record the rotation angles and the output laser powers. Fit the angle vs power curve with a sinusoidal function; the maximum output power position of polarizer B is 0° azimuthal angle position (see Figure 1).
2. Set up the reference directions for the azimuthal angles of the waveplates
- Put an HWP into the beam path between polarizer A and polarizer B and rotate the HWP to maximize the output power. The azimuthal angle of the optical axis of the HWP is then 0°.
- Use a stepper motor rotation stage to hold the HWP and put the power meter behind polarizer B to record the rotation angles and the output laser powers. Fit the angle vs power curve with a sinusoidal function; the maximum output power position of the HWP is 0° azimuthal angle.
- Put a QWP into the beam path between the HWP and polarizer B, rotate the QWP to maximize the output power. The azimuthal angle of the optical axis of the QWP is then 0°.
- Use a stepper motor rotation stage to hold the QWP and put the power meter behind polarizer B to record the rotation angles and the output laser powers. Fit the angle vs power curve with a sinusoidal function; the maximum output power position of the QWP is 0° azimuthal angle position.
- Remove polarizer B and the power meter from the beam path. Use two mirrors to direct laser beam into the vacuum chamber that houses an ion trap to interact with 25Mg+ ions.
NOTE: The laser propagation direction should be along the magnetic field direction inside the vacuum chamber. A magnetic field is used to define the quantization axis of the ions.
3. Doppler cooling of single 25Mg+ ions
- Turn on the 532 nm ablation laser, which is a Q-switched Nd:YAG laser. Its repetition rate is 1 kHz, with pulse energy of 150 µJ. The ablation laser irradiates a magnesium wire target surface inside the vacuum chamber, and then magnesium (Mg) atoms are ejected from the target surface.
NOTE: The power supply for the ion trap should be turned on. - At the same time, turn on the 285 nm ionization laser to ionized Mg atoms. The ionization laser is a fourth harmonic laser with an output power of 1 mW. The ionization laser will illuminate the center of the ion trap.
- Make sure only one ion is trapped in the ion trap by looking at the image of an electron multiplied charged coupled device (EMCCD). An example image showing trapped ions is shown in Figure 2. Each bright spot is one ion. If there is more than one ion in the trap, turn off the power supply of the ion trap to release the ions. Then repeat steps 3.1-3.2 until only one (i.e., single) ion is trapped.
NOTE: The homemade imaging system of the EMCCD consists of four lenses, and its magnification is 10x. The ion spacing is about 2-10 µm and the pixel spacing of the EMCCD is 16 µm. The EMCCD can, therefore, be used to identify the existence of one single ion. - Set the magnetic field to be 6.5 Gauss by adjusting the current of Helmholtz coils. The magnetic field is measured by comparing the different frequencies between the two ground state transitions,
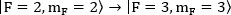 and
and 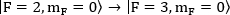 . For details of the method please refer11.
. For details of the method please refer11.
4. Lock the 280 nm Doppler cooling laser frequency to a wavelength meter12
- Scan the frequency of the 280 nm laser and count the fluorescence photon numbers collected by a photon multiplier tube (PMT) by a frequency counter. At the same time, record the frequency of the laser using a wavelength meter. Find the resonant frequency ν0 where the fluorescence rate reaches a maximum.
NOTE: The fluorescence counts will increase when the laser frequency is moving close to the ion resonant frequency and will reach a maximum at the resonant frequency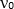 .
. - Lock the laser frequency to the wavelength meter using a digital servo control program that is running on an accompanying computer. Click on the Lock button on the program graphic interface when the wavelength meter shows a reading of
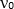 .
.
5. Set the intensity of the laser to equal the saturation intensity12
- Change the power of the laser by adjusting the driving power of an acousto-optic-modulator (AOM), which is used in the beam path to change the frequency and power of the laser. Record the power and the fluorescence counts.
- Fit the curve of the power and the fluorescence counts with Equation (6), and obtain the saturation power
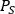 .
. - Set the laser power to
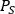 by adjusting the driving power of the AOM.
by adjusting the driving power of the AOM.
6. Measure the birefringence of the vacuum window.
- Alternately, adjust the azimuthal angles of the HWP and the QWP to maximize the fluorescence counts. Record the azimuthal angles of the HWP and the QWP at maximum counts, which are α and β.
- Use the stepper motor rotation stages to rotate the HWP and the QWP and record the rotation angles and the corresponding fluorescence counts.
- Use Equation (4) and Equation (5) to calculate the birefringence of the vacuum window θ and
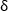 .
.
Access restricted. Please log in or start a trial to view this content.
Results
Figure 3 shows the beam path of the experiment. Polarizer B in Figure 3a is removed after angle initialization (Figure 3b). The laser passed through a polarizer, an HWP, a QWP, and the vacuum window, sequentially. The Stokes vector of laser is 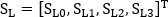 , where
, where
Access restricted. Please log in or start a trial to view this content.
Discussion
This manuscript describes a method to perform in situ measurement of the birefringence of the vacuum window and the polarization states of the laser light inside the vacuum chamber. By adjusting the azimuthal angles of the HWP and the QWP (α and β), the effect of the birefringence of the vacuum window (δ and θ) can be compensated so that the laser inside the vacuum chamber is a pure circularly polarized light. At this point, there exists a definite relationship between the birefringence of the vacuum ...
Access restricted. Please log in or start a trial to view this content.
Disclosures
The authors have nothing to disclose.
Acknowledgements
This work was partially supported by the National Key R&D Program of China (Grant No. 2017YFA0304401) and the National Natural Science Foundation of China (Grant Nos. 11774108, 91336213, and 61875065).
Access restricted. Please log in or start a trial to view this content.
Materials
| Name | Company | Catalog Number | Comments |
| 280 nm Doppler cooling laser | Toptica | SYST DL-FHG Pro 280 | Doppler cooling laser |
| 285 nm ionization laser | Toptica | SYST DL-FHG Pro 285 | ionization laser |
| Ablation laser | Changchun New Industries Optoelectronics Technology | EL-532-1.5W | Q-switched Nd:YAG laser |
| AOM | Gooch & Housego | AOMO 3200-1220 | wavelengh down to 257 nm |
| EMCCD camera | Andor | iXon3 897 | imaging of 25Mg+ in ion trap |
| Glan-Taylor polarizer | Union Optic | Custom | distinction ratio 1e-6 |
| Half waveplate | Union Optic | Custom | made of quartz |
| Photon multiplier tube | Hamamatsu | H8259-09 | fluorescent counting |
| Power meter | Thorlabs | PM100D | laser power monitor |
| Quarter waveplate | Union Optic | Custom | made of quartz |
| Mirror | Union Optic | Custom | dielectric coated for 280 nm |
| Stepper motor roation stage | Thorlabs | K10CR1/M | rotating wave plates |
| Vacuum chamber | Kimball Physics | MCF800-SphSq-G2E4C4 | made of Titanium |
| Vacuum window | Union Optic | Custom | made of fused silica |
References
- Robens, C., et al. High-Precision Optical Polarization Synthesizer for Ultracold-Atom Experiments. Physical Review A. 9 (3), 34016(2018).
- Cairncross, W. B., et al. Precision Measurement of the Electron's Electric Dipole Moment Using Trapped Molecular Ions. Physical Review Letters. 119 (15), 153001(2017).
- Bougas, L., et al. Fundamentals of cavity-enhanced polarimetry for parity-nonconserving optical rotation measurements: Application to Xe, Hg, and I. Physical Review A. 89 (5), 52127(2014).
- Bragin, S., et al. High-Energy Vacuum Birefringence and Dichroism in an Ultra-strong Laser Field. Physical Review Letters. 119 (25), 250403(2017).
- Nicholson, T. L., et al. Systematic evaluation of an atomic clock at total uncertainty. Nature Communications. 6, 6896(2015).
- Roos, C. F., et al. Revealing Quantum Statistics with a Pair of Distant Atoms. Physical Review Letters. 119 (16), 160401(2017).
- Saulius, J., et al. High-efficiency optical transfer of torque to a nematic liquid crystal droplet. Applied Physics Letters. 82, 4657(2003).
- Zhu, K., et al. Absolute polarization measurement using a vector light shift. Physical Review Letters. 111 (24), 243006(2013).
- Steffen, A., et al. Note: In situ measurement of vacuum window birefringence by atomic spectroscopy. Review of Scientific Instruments. 84 (12), 126103(2013).
- Yuan, W. H., et al. A simple method for in situ measurement of vacuum window birefringence. Review of Scientific Instruments. 90 (11), 113001(2019).
- Xu, Z. T., et al. Precision measurement of the 25Mg+ ground-state hyperfine constant. Physical Review A. 96 (5), 052507(2017).
- Zhang, J., et al. A long-term frequency stabilized deep ultraviolet laser for Mg+ ions trapping experiments. Review of Scientific Instruments. 84 (12), 123109(2013).
- Yuan, W. H., et al. Precision measurement of the light shift of 25Mg+ ions. Physical Review A. 98 (5), 52507(2018).
- Loudon, R. The Quantum Theory of Light, 3rd ed. , Oxford University Press. New York. (2000).
- Hu, Z. K., et al. Demonstration of an ultrahigh-sensitivity atom-interferometry absolute gravimeter. Physical Review A. 88 (4), 043610(2013).
Access restricted. Please log in or start a trial to view this content.
Reprints and Permissions
Request permission to reuse the text or figures of this JoVE article
Request PermissionThis article has been published
Video Coming Soon
Copyright © 2025 MyJoVE Corporation. All rights reserved