Sınırlanmamış ve Sınırlı Yüzey Aktif Bazlı Kesme Viskoelastik Sıvılarda Küresel Parçacıkların Yerleşme Hızının Deneysel Ölçümü

Özet

Bu makale, yüzey aktif bazlı kesme inceltme viskoelastik sıvılarındaki küresel parçacıkların terminal çökeltme hızlarını ölçmek için deneysel prosedürü göstermektedir. Çok çeşitli reolojik özellikler üzerindeki sıvılar hazırlanır ve paralel duvarlar arasındaki sınırsız sıvılarda ve sıvılarda bir dizi parçacık boyutu için çökeltme hızları ölçülür.

Özet

Yüzey aktif bazlı kesme inceltme viskoelastik (VES) sıvılarındaki küresel parçacıkların terminal çökeltme hızlarını ölçmek için deneysel bir çalışma gerçekleştirilir. Ölçümler, paralel duvarlar arasındaki sınırsız sıvılara ve sıvılara yerleşen parçacıklar için yapılır. Çok çeşitli reolojik özelliklere sahip VES sıvıları hazırlanır ve reolojik olarak karakterize edilir. Reolojik karakterizasyon, viskoz ve elastik özellikleri ölçmek için sırasıyla sabit kesme viskozitesi ve dinamik salınımlı kesme ölçümlerini içerir. Sınırsız koşullar altında yerleşme hızları, parçacıkların çapının en az 25 katını çapına sahip gagalarla ölçülür. Paralel duvarlar arasındaki yerleşme hızlarını ölçmek için, farklı duvar aralığına sahip iki deneysel hücre inşa edilir. Değişen boyutlardaki küresel parçacıklar sıvılara hafifçe bırakılır ve yerleşmesine izin verilir. İşlem yüksek çözünürlüklü bir video kamera ile kaydedilir ve parçacığın yörüngesi görüntü analiz yazılımı kullanılarak kaydedilir. Terminal yerleştirme hızları verilerden hesaplanır.

Elastikiyetin sınırsız sıvılardaki yerleşme hızı üzerindeki etkisi, deneysel yerleşme hızı ile Renaud ve arkadaşlarının inelastik sürükleme tahminleri tarafından hesaplanan yerleşme hızı karşılaştırılarak ölçülür. ¹ Sonuçlar, sıvıların elastikiyetinin yerleşme hızını artırabileceğini veya azaltabileceğini göstermektedir. Azaltma/artırmanın büyüklüğü, sıvıların reolojik özelliklerinin ve parçacıkların özelliklerinin bir işlevidir. Hapseden duvarların yerleşme üzerinde gerilik etkisine neden olduğu gözlenir ve gerilik duvar faktörleri açısından ölçülür.

Giriş

Sıvılardaki parçacıkların süspansiyonları, farmasötik üretim, atık su arıtımı, uzay itici reenjeksiyonu, yarı iletken işleme ve sıvı deterjan üretimi gibi uygulamalarda karşılaşılmıştır. Petrol endüstrisinde, viskoelastik kırılma sıvıları hidrolik kırıklarda proppantları (tipik olarak kum) taşımak için kullanılır. Proppantların pompalanması durdurulması üzerine kırığı açık tutun ve hidrokarbonların geri akması için iletken bir yol sağlayın.

Parçacıkların yerleştirilmesi, sıvının reolojisi ve yoğunluğu, parçacıkların büyüklüğü, şekli ve yoğunluğu ve sınırlı duvarların etkisi ile yönetilir. Sürünen akış rejiminde bir Newton sıvısına yerleşen küresel bir parçacık için, yerleşme hızı 1851'de Stokes tarafından türetilen Stokes denklemi tarafından verilir. Daha yüksek Reynolds sayılarındaki sürükleme kuvvetini hesaplamak için ifadeler sonraki araştırmacılar tarafından^2-6. Sınırlama duvarları, parçacıklar üzerinde gerilik etkisi uygulayarak yerleşme hızlarını azaltır. Duvar faktörü, F_w, sınırlandırılmamış koşullar altında sınırlanan duvarların varlığında terminal yerleştirme hızının çökeltme hızına oranı olarak tanımlanır. Duvar faktörü, hapsedici duvarların gerilik etkisini ölçendir. Çok çeşitli Reynolds sayıları üzerinde farklı kesit tüplerinde Newton sıvılarına yerleşen küreler için duvar faktörlerini belirlemek için birçok teorik ve deneysel çalışma literatürde^{mevcuttur 7-13}. Sonuç olarak, Newton sıvılarındaki kürelerdeki sürüklenmeyi belirlemek için geniş bir bilgi gövdesi vardır.

Özellikle viskoelastik sıvılar olmak üzere, Yenimyen olmayan sıvılardaki parçacıkların yerleşme hızının belirlenmesine yönelik geçmiş çalışmalar daha az tamamlanmaktadır. Çeşitli sayısal tahminler^14-18 ve deneysel çalışmalar^19-24 inelastik güç-hukuk sıvılarında bir küre üzerindeki sürükleme kuvvetini belirlemek için literatürde mevcuttur. Tripathi ve arkadaşlarının teorik tahminlerini kullanarak. ¹⁵ ve Tripathi ve Chhabra¹⁷, Renaud ve ark. ^1, inelastik güç-hukuk sıvılarındaki sürükleme katsayısını(C_D)hesaplamak için aşağıdaki ifadeleri geliştirdi.

Re_PL<0.1 için (sürünen akış rejimi)

burada X(n) sürükleme düzeltme faktörü^{13 'dür.} Re_PL,aşağıdaki gibi tanımlanan bir güç yasası sıvısına düşen bir kürenin Reynolds numarasıdır:

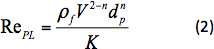
burada f sıvının yoğunluğudur. Sürükleme düzeltme faktörü aşağıdaki denklem¹ile donatılmıştır:

Sürükleme katsayısı tanımı kullanılarak, yerleştirme hızı şu şekilde hesaplanır:

0.1 için_PL<100

burada X, yüzey alanının parçacığın öngörülen alanına oranıdır ve küreler için 4'e eşittir. C_D0, Denklem 1 , C_{D∞ tarafından} verilen Stokes bölgesindeki sürükleme katsayısıdır (Re_PL < 0.1),Newton bölgesindeki sürükleme katsayısının değeridir (Re_PL > 5 x 10²⁾ve 0.44'e eşittir. β, b, k parametreleri şu şekilde ifade edilir:

α_o = 3 ve α, X(n) ile ilgili ortalama kesme hızının düzeltmesidir:

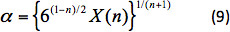
Yerleştirme hızını hesaplamak için boyutsuz grup N_d ²⁵ kullanılır:

N_d, yerleştirme hızından bağımsızdır ve açıkça hesaplanabilir. Bu değer ve Denklem 5, Re_PL'deki sürükleme katsayısı ifadesi kullanılarak yinelemeli olarak çözülebilir. Yerleştirme hızı daha sonra aşağıdakiler kullanılarak hesaplanabilir:

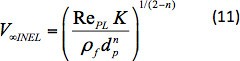
Denklemler 1-9'daki ifadeler 1 ≥ n ≥ 0.4 değerleri için elde edilen teorik tahminlere dayanıyordu. Chhabra^13, yukarıdaki ifadelerden elde edilen tahminleri Shah^{26-27 (n 0.281-0.762} arasında değişen) ve Ford ve ark.'ın deneysel sonuçlarıyla karşılaştırdı. ²⁸ (n 0.06-0.29 arasında değişik). İfadelerin sürükleme katsayılarını doğru tahmin etmek için gösterildiği gösterilmiştir. Bu analizlere dayanarak, yukarıdaki formülasyon, küresel parçacıkların 1 ≥ n ≥ 0,06 için inelastik güç-hukuk sıvılarındaki çökeltme hızını hesaplamak için kullanılabilir. Bu tahmin edilen inelastik güç-hukuk sıvılarındaki yerleşme hızı, sıvı elastikiyetinin yerleşme hızı üzerindeki etkisini belirlemek için güç-hukuk viskoelastik sıvılarındaki deneysel hız ile karşılaştırılır. Ayrıntılı adımlar bir sonraki bölümde belirtilmiştir.

Viskoelastik sıvılardaki parçacıkların yerleşme hızının belirlenmesi de farklı araştırmacılar tarafından değişen gözlemlerle araştırma konusu olmuştur; (i) Sürünen akış rejiminde kesme inceltme efektleri viskoelastik etkileri tamamen gölgede bırakıyor ve yerleşme hızları tamamen viskoz teorilerle mükemmel bir şekilde uyuşmaktadır^29-32, (ii) parçacık deneyimi sürünen akış rejiminde ve dışında bir sürükleme azaltma ve yerleştirme hızları elastikiyet nedeniyle artar^30,33,34, (iii) sıvı esnekliği nedeniyle yerleşme hızı azaltır³⁵. Walters ve Tanner^36, Boger sıvıları (sabit viskozite elastik sıvılar) elastikiyeti için düşük Weissenberg sayılarında sürükleme azalmasına ve ardından daha yüksek Weissenberg sayılarında sürükleme artışına neden olduğunu özetledi. McKinley^37, kürenin ardından gelen uzatma etkilerinin weissenberg sayılarında sürüklenme artışına neden olduğunu vurguladı. Chhabra^13, parçacıkların sınırsız ve sınırlı viskoelastik sıvılara yerleştirilmesine ilişkin önceki çalışmaların kapsamlı bir incelemesinin ardından, teorik gelişmelerde kesme hızına bağımlı viskozitenin gerçekçi bir tanımını sıvı esnekliği ile birleştirmenin zorluğunu vurgulamıştır. Küresel parçacıkların yerleşmesi üzerindeki duvar etkilerinin incelenmesi de son yıllarda bir araştırma alanı olmuştur^38-42. Bununla birlikte, tüm çalışmalar silindirik tüplerdeki küresel parçacıkların yerleştirilmesi üzerine yapılmıştır. Paralel duvarlar arasındaki viskoelastik sıvılara yerleşen küresel parçacıklar için veri mevcut değildir.

Bu çalışma, kürelerin kesme inceltici viskoelastik sıvılara yerleştirilmesini deneysel olarak incelemeye çalışır. Bu deneysel çalışmanın amacı, sıvı elastikiyetinin, kesme inceltme ve duvarların, kesme inceltme viskoelastik sıvılarda küresel parçacıkların yerleşme hızı üzerindeki etkisini anlamaktır. Bu makale, bazı temsili sonuçlarla birlikte bu çalışma için kullanılan deneysel yöntemlere odaklanmıştır. Analizlerle birlikte ayrıntılı sonuçlar daha önceki bir yayında bulunabilir⁴³.

Access restricted. Please log in or start a trial to view this content.

Protokol

1. Sıvıların Hazırlanması

Bu deneysel çalışma için polimer içermeyen, viskoelastik, iki bileşenli, yüzey aktif bazlı bir sıvı sistemi kullanılmaktadır. Bu sıvı sistemi, hidrolik kırma tedavileri için birçok üretim alanında petrol ve gaz kuyularında kullanılmıştır^44,45. Bu akışkan sistemi optik olarak şeffaf olduğu ve reolojinin iki bileşenin konsantrasyonları ve oranları sistematik olarak değiştirilerek kontrol edilebildiği için bu çalışma için kullanılmaktadır. Akışkan sistemi, A bileşeni olarak bir anionik yüzey aktif maddeden (sodyum ksilen sülfonat gibi) ve B bileşeni olarak katyonik bir yüzey aktif maddeden (N,N,N-trimetil-1-octadecamonium klorür gibi) oluşur.

1. Damıtılmış suya belirli bir A bileşeni konsantrasyonu ekleyin ve uygun karıştırmayı sağlamak için bir havai karıştırıcı kullanarak yüksek devirde karıştırın. 2-3 dakika karıştırmasına izin verin.
2. Bu karışıma belirli bir B bileşeni konsantrasyonu ekleyin ve 2-3 dakika daha karışmasına izin verin.
3. Hava kabarcıklarını boşaltmak için karışımı 2-6 saat dinlendirin. Not: Son sıvı karışımı optik olarak şeffaftır. Bu çalışma için farklı konsantrasyonlarda yedi sıvı karışımı kullanılmaktadır. Konsantrasyonlar, çok çeşitli viskozitelerde sıvı karışımı elde etmek için seçilir.

2. Sınırsız Sıvılarda Yerleşme Hızlarının Ölçütlen 5

1-5 mm arasında değişen çaplarda cam küreler kullanılır.

1. Cam kürelerin çapını ölçmek için yüksek çözünürlüklü bir mikroskop kullanın. Kürelerin pürüzsüz yüzeylere sahip olduğundan ve mükemmele yakın küreler olduğundan emin olun.
2. Sıvıyı, sınırlama duvarlarının parçacıkların çökeltme hızı üzerinde bir etkisi olmadığından emin olmak için parçacıkların çapının en az 25 katını taşıyan cam kaplarda saklayın.
3. Laboratuvar termometresi kullanarak oda sıcaklığını ve sıvı sıcaklığını kaydedin. Sıcaklığın ölçümü önemlidir, çünkü sıvının reolojik ölçümleri çökeltme deneyinin yapıldığı sıcaklıkta yapılmalıdır.
4. Kabın yanına bir metre çubuğu yerleştirin.
5. Cam parçacığını yavaşça sıvıya batırın ve yerleşmesine izin verin. Yerleştirme işlemini yüksek çözünürlüklü bir video kamera ile kaydedin.
6. Bir görüntü analizi uygulaması kullanarak kaydedilen videodan farklı zaman adımlarında parçacığın konumunu izleyin. Not: Bu çalışmada ,'Tracker' adlı bir yazılım uygulaması kullanılır (http://www.cabrillo.edu/~dbrown/tracker/).
7. Parçacığın zamana karşı dikey konumunu çizin ve hattın eğiminden terminal yerleştirme hızını hesaplayın.
8. Tekrarlanabilirliği sağlamak için denemeyi en az 3 kat benzersiz koşullar kümesi altında tekrarlayın. Farklı ölçümler için görüntü analizini gerçekleştirin ve hata çubukları kullanarak belirli bir sıvıdaki belirli bir parçacık çapı için yerleştirme hızını bildirin.
9. Farklı çaplı parçacıklar için yukarıdaki adımları tekrarlayın ve çökeltme hızlarını kaydedin. Çökeltme hızını parçacık çapına karşı çizin. Not: Şekil 1, bir sıvıda beş farklı boyutta parçacığın yerleşme hızını gösterir.

3. Paralel Duvarlar Arasındaki Sıvılar için Yerleşme Hızlarının Ölçümü

Paralel duvarların varlığındaki yerleşme hızlarını ölçmek için Pleksiglastan yapılmış iki deneysel hücre kullanılır.

1. Hücreyi tasarlarken ve inşa ederken, duvarların pürüzsüz ve birbirine mükemmel bir şekilde paralel olduğundan emin olun. Duvarların ortogonal paralel duvarlara etkisinin olmadığından emin olmak için hücrelerin en boy oranını düşük tutun. Not: Bu çalışmada iki hücredeki duvarlar arasındaki boşluk sırasıyla 3,6 mm ve 8 mm'dir. Şekil 2 bir deneysel hücrenin şemasını göstermektedir.
2. Hücreyi sıvı ile doldurun ve hücredeki parçacığı giriş/çıkış portunda hafifçe serbest bırakın. Giriş/çıkış portunun lastik bir durdurucu ile kapatılmasını ve hücrenin ortasına ulaşana kadar parçacığın yerleşmesini sağlar.
3. Bu noktada, hücreyi dikkatlice dikey olarak konumlandırın ve parçacığın yerleşmesine izin verin.
4. Hücrenin yanına bir metre çubuğu yerleştirin ve yüksek çözünürlüklü video kamerayı kullanarak yerleştirmeyi kaydedin.
5. Laboratuvar termometresi kullanarak oda sıcaklığını ve sıvı sıcaklığını kaydedin. Bu önemlidir çünkü sıvının reolojik ölçümleri bu sıcaklıkta yapılmalıdır.
6. Sınırsız yerleştirme hızı ölçümlerinde olduğu gibi, yazılım uygulaması 'Tracker'daki yerleştirme hızını ölçün. Tekrarlanabilirliği sağlamak ve her ölçümde hata çubukları elde etmek için ölçümleri en az üç kez tekrarlayın.

4. Sıvıların Reolojik Karakterizasyonu

1. Kesme hızının bir fonksiyonu olarak sıvının viskozitesini ölçmek için sabit kesme viskozitesi ölçümlerini gerçekleştirin. Not: Bu çalışmada, çift duvarlı eşmerkezli silindir fikstürüne sahip TA Instruments tarafından ARES reometresi (iç kap çapı: 27,95 mm, bob çapı içinde: 29,50 mm, bob çapı dışında: 32,00 mm, dış bardak çapı: 34,00 mm, bob uzunluğu: 32,00 mm) kullanılır.
2. Kesme oranını 0,1-800 sn^-1 arasında değiştirin ve 10 noktada/on yılda ölçümler alın. Kabın sıcaklığının, yerleştirme deneyinin aynı sıvıda yapıldığı sıcaklıkla aynı olduğundan emin olun. Şekil 3, günlük günlüğü çiziminde bir akışkan örneği için viskozite ile kesme oranını gösterir.
3. Aynı sıvı için, parçacıkların yerleştirme deneylerinde karşılaştıkları kesme hızı aralığını hesaplayın. 2V/d_p 20,23 ile tanımlanan yüzey ortalama parçacık kesme hızını kullanın, burada V parçacığın çökelme hızıdır ve d_p parçacık çapıdır.
4. Viskoziteye karşı kesme hızı grafiğindeki bu kesme hızları aralığına μ=Kφ^n-1güç yasası eğrisi takın. Günlük günlüğü çiziminde bu sığdırma düz bir çizgi olacaktır. K (akış tutarlılığı indeksi) ve n (akış davranışı dizini) parametrelerini belirleyin.
   K ve n sıvıların viskozitesini ölçer. Şekil 3, aynı arsaya sığdırılan güç yasasını göstermektedir.
5. 0,1-100 rad/sn frekans aralığında dinamik salınımlı kesme ölçümlerini gerçekleştirin ve elastik modül, G' ve viskoz modül, G'' ölçün. 10 noktada/on yılda ölçüm alın.
   Şekil 4'te sıvı örneği için G' ve G'' gösterilir.
6. Bu verilerden G''/G' olmak üzere iki modüllünün oranını hesaplayın. Bir regresyon analizi kullanarak modüler oranını bir Maxwell modeline sığdırın ve sıvının gevşeme süresini (φ) hesaplayın. Bir Maxwell modeli için iki modül oranı için denklem^46,47' dir:

Sıvının gevşeme süresi, sıvının esnekliğini ölçen bir süredir. Gevşeme süresinden daha fazla, daha elastik sıvıdır. Şekil 5, Maxwell uyumu ile birlikte sıvı örneği için G ''/G''sini gösterir. Bağlantı, frekans aralığı üzerindeki varyans ölçüsünün toplamını en aza indirerek gerçekleştirilir.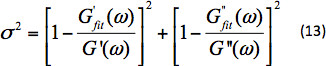

5. Elastikiyetin Sınırsız Yerleşme Hızları Üzerindeki Etkisinin Belirlenmesi

1. V_∞VE tarafından sınırsız sıvıdaki bir parçacığın deneysel çökeltme hızını gösterir, burada '∞VE' unconfined viskoelastik sıvıları ifade eder. Bu deneysel yerleşme hızını, güç kanunu parametrelerine dayalı görünür viskozite verilerine dayanarak hesaplanan çökeltme hızı (V_∞INEL) ile karşılaştırın. Renaud ve arkadaşları tarafından geliştirilen ifadeleri kullanın. V_∞INELhesaplamak için ^1. İfadeler Giriş bölümünde belirtilmiştir. '∞INEL', tanımlanmamış inelastik sıvıları ifade eder.
2. V_∞EL/V_∞INEL oranını hesaplayın ve hız oranı olarak orana bakın.
   Hız oranının değeri, esnekliğin yerleşme hızı üzerindeki etkisini göstermektedir. 1'den büyük hız oranı, sıvı esnekliği nedeniyle hız artışı / sürükleme azalmasını önerir. 1'den küçük hız oranı, sıvı esnekliği nedeniyle hız azaltma/sürükleme artışı olduğunu göstermektedir.
3. Farklı çapındaki parçacıkların farklı romatoloji akışkanlarındaki yerleşim hızı üzerindeki elastikiyetin etkisini gözlemlemek için farklı sıvılar için parçacık çapının bir işlevi olarak hız oranını çizin. Şekil 6, sıvılardan birinde parçacık çapının bir fonksiyonu olarak hız oranını göstermektedir.

6. Paralel Duvarların Yerleşme Hızlarındaki Gerilik Etkisinin Ölçülmesi

1. Paralel duvarların varlığında yerleşme hızını bölerek belirli bir çap parçacığı için F_w, V_∞VE'yi sınırsız sıvıdaki çökeltme hızına bölerek duvar faktörünü hesaplayın, V_∞VE.
2. Belirli bir sıvı için, parçacık çapının duvar aralığı oranına bir işlevi olarak duvar faktörlerini çizin, r. Şekil 7, sıvılardan birine yerleşen parçacıkların duvar faktörlerini göstermektedir. Arsa, hapsedici duvarların yerleşme hızı üzerindeki gerilik etkisini ölçmeye yardımcı olur. Duvar faktörünü düşürün, duvar geriliği etkisini daha yüksek.

Access restricted. Please log in or start a trial to view this content.

Sonuçlar

Deneyler, benzersiz K, n ve φ değerlerine sahip yedi farklı sıvı karışımında beş farklı çaplı parçacık için gerçekleştirilir. Şekil 1, bir sıvıdaki parçacık çapının bir işlevi olarak yerleşme hızını gösterir. Hata çubukları üç ölçümdeki değişkenliği gösterir. Deney sırasında ölçülen oda sıcaklığı 23 °C'dir. Çökeltme hızlarının parçac?...

Access restricted. Please log in or start a trial to view this content.

Tartışmalar

Deneysel çalışma, düzleştirici viskoelastik sıvılardaki küresel parçacıkların yerleşim hızlarının sınırlanmamış ve sınırlı koşullar altında ölçüldüğünü belirlemeye odaklanmaktadır. Yerleşme hızlarının tekrarlanabilir ölçümlerini elde etmek için ayrıntılı deneysel prosedür sunulmuştur. Sonuçlar, sıvı elastikiyetinin yerleşme hızını artırabileceğini veya azaltabileceğini göstermektedir. Duvarlar yerleşme üzerinde gerilik etkisi uygular ve bu etki duvar faktörleri a...

Access restricted. Please log in or start a trial to view this content.

Malzemeler

Name	Company	Catalog Number	Comments
Glass Microspheres	Whitehouse Scientific	#GP1750	Available in different sieve fractions.
Rheometer	TA Instruments	ARES	Any standard rheometer capable of taking dynamic and static measurements
Anionic Surfactant (Component A)		Proprietary fluid	Used in oil field services for hydraulic fracturing. Sodium Xylene Sulfonate can be used as a substitute.
Cationic Surfactant (Component B)		Proprietary fluid	Used in oil field services for hydraulic fractuing. N,N,N-Trimethyl-1-Octadecamonium Chloride can be used as a substitute.