Экспериментальное измерение скорости урегулирования сферических частиц в неограниченных и ограниченных Surfactant основе стрижки тоньше вискоэластических жидкостей

Резюме

В настоящем документе демонстрируется экспериментальная процедура измерения терминальных скоростей оседающих сферических частиц в истончении вязко-вязко-жидких жидкостей на основе сурфактанта. Готовятся жидкости по широкому спектру реологических свойств, и скорость заселения измеряется по ряду размеров частиц в несырьях жидкостях и жидкостях между параллельными стенками.

Аннотация

Экспериментальное исследование проводится для измерения терминальной оседают скорости сферических частиц в сурфактант основе стрижки истончение вязко-вязко-упругих (VES) жидкостей. Измерения проводятся для частиц, осеханых в несыханых жидкостях и жидкостях между параллельными стенами. Ves жидкости по широкому кругу реологических свойств подготовлены и реологически охарактеризованы. Реологическая характеристика включает в себя устойчивую вязкость и динамические измерения колебаний и стрижки для количественной оценки вязких и эластичные свойства соответственно. Скорость заселения в несыхех условиях измеряется в стаканах диаметром не менее 25 раз диаметр частиц. Для измерения скорости заселения между параллельными стенами строятся две экспериментальные клетки с разным интервалом между стенами. Сферические частицы различных размеров аккуратно опускаются в жидкости и могут осесть. Процесс записывается с помощью видеокамеры высокого разрешения и траектория частицы записывается с помощью программного обеспечения анализа изображений. Скорость урегулирования терминала рассчитывается на основе данных.

Влияние эластичности на оседают скорости в неограниченных жидкостях количественно, сравнивая экспериментальную скорость урегулирования урегулирования к расчетной скорости рассчитывается неупругой перетащить прогнозы Рено и др. ¹ Результаты показывают, что эластичность жидкостей может увеличить или уменьшить скорость заселения. Величина сокращения/увеличения является функцией реологических свойств жидкостей и свойств частиц. Считается, что ограничение стен вызывает эффект задержки при заселении, а задержка измеряется с точки зрения факторов стены.

Введение

Подвески частиц в жидкостях встречаются в таких приложениях, как фармацевтическое производство, очистка сточных вод, реинъекция космического топлива, полупроводниковая обработка и производство жидких моющих средств. В нефтяной промышленности вязко-вязко-гРП используются для транспортировки проппантов (обычно песка) при гидравлических переломах. После прекращения перекачки проппанты держат перелом открытым и обеспечивают проводящий путь для углеводородов, чтобы течь обратно.

Урегулирование частиц регулируется реологией и плотностью жидкости, размером, формой и плотностью частиц и эффектом ограничивающих стенок. Для сферической частицы, оседаемой в ньютоновской жидкости в режиме ползучего потока, скорость заселения дается уравнением Стокса, полученным Стокса в 1851 году. Выражения для расчета силы сопротивления на более высоких числах Рейнольдса были представлены последующими^{исследователями 2-6}. Ограничение стенок снижает скорость заселения, оказывая эффект задержки на частицы. Фактор стены, F_w, определен как отношение терминальной заселяя скорости в присутствии ограничивая стен к устанавливать скорость под unbounded условиями. Фактор стены количественно определяет эффект задержки ограничивающихся стен. Много теоретических и экспериментальных изучений для того чтобы обусловить факторы стены для сфер устанавливать в ньютоновских жидкостях в по-разному перекрестных пробках над широким рядом номеров Reynolds^{имеющиеся в словесности 7-13}. В целом, имеется обширный информационный ресурс для определения сопротивления сфер в ньютоновских жидкостях.

Прошедшая работа по определению скорости заселения частиц в ненютонийских жидкостях, особенно вискоэластической жидкости, менее завершена. Различные численные^{прогнозы 14-18} и^{экспериментальные исследования 19-24 доступны} в литературе, чтобы определить силу сопротивления на сфере в неуясных жидкостях силового права. Используя теоретические прогнозы Tripathi et al. ¹⁵ и Тривати и Чхабра¹⁷, Рено и др. ¹ разработал следующие выражения для расчета коэффициента сопротивления(C_D)в неупомященных жидкостях power-law.

Для Re_PL<0.1 (режим ползучего потока)

где X(n) является фактором коррекции сопротивления¹³. Re_{PL —}это число Рейнольдса для сферы, впадая в жидкость закона власти, определяемую как:

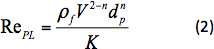
где f_{является} плотность жидкости. Коэффициент коррекции сопротивления был оснащен следующим уравнением^1:

Используя определение коэффициента сопротивления, скорость заселения рассчитывается как:

За 0,1_PL<100

где X является отношением площади поверхности к проецируемой области частицы и равен 4 для сфер. C_D0 — это коэффициент сопротивления в регионе Стокса (Re_PL < 0,1), данный Equation 1, C_{D∞ —} это значение коэффициента сопротивления в регионе Ньютона (Re_PL > 5 x 10²⁾и равно 0,44. Параметры β, b, k выражены как:

α_{о No} 3 и α коррекция для среднего уровня стрижки, связанные с X(n) как:

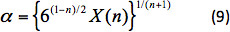
Для расчета расчетной скорости используется беза измерений группа N_d ^25:

N_d не зависит от расчетной скорости и может быть рассчитан явно. Используя это значение и выражение коэффициента сопротивления в Equation 5, Re_PL может быть решена итеративно. Скорость урегулирования может быть рассчитана с помощью:

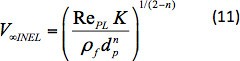
Выражения в уравнениях 1-9 основывались на теоретических прогнозах, полученных для значений 1 ≥ n ≥ 0,4. Chhabra^{13 сравнил} прогнозы из вышеуказанных выражений с экспериментальными результатами Шах^26-27 (n варьировался от 0,281-0,762) и Ford и др. ²⁸ (n варьировался от 0,06-0,29). Были показаны выражения, точно предсказывая коэффициенты сопротивления. На основе этих анализов вышеупомященная формулировка может быть использована для расчета скорости заселения сферических частиц в неуясных жидкостях power-law в течение 1 ≥ n ≥ 0,06. Это предсказало урегулирования скорости в неупругой жидкости power-law сравнивается с экспериментальной скоростью в вязкоэластичных жидкостях вискоэлестического закона власти, чтобы определить влияние эластичности жидкости на расчет скорости. Подробные шаги упоминаются в следующем разделе.

Определение скорости заселения частиц в вязко-вязкостачных жидкостях также было предметом исследований с различными наблюдениями различных исследователей; i) В режиме ползучего потока эффекты истончения снопывания полностью затмевают вязко-вязкие эффекты и оседают скорости находятся в отличном согласии^{с чисто вязкими теориями 29-32}, (ii) частицы испытывают уменьшение сопротивления в режиме ползучего потока и за его пределами, а скорость заселения увеличивается из-за эластичности^30,33,34, (iii)^{уровень оседает из-за эластичности 35.} Уолтерс и Таннер^{36 подытожил,} что для Boger жидкости (постоянная вязкая вязкая жидкость) эластичность вызывает снижение сопротивления на низких числах Weissenberg следуют перетащить повышение на более высокие номера Weissenberg. McKinley^{37 подчеркнул,} что расширение эффектов в результате сферы причиной сопротивления увеличение на более высокие номера Weissenberg. После всестороннего обзора предыдущей работы по урегулированию частиц в неограниченных и ограниченных вязкоэластичных жидкостях, Chhabra^{13 подчеркнула проблему} включения реалистичного описания зависимой вязкости скорости сдвига вместе с эластичностью жидкости в теоретических разработках. Изучение влияния стен на заселку сферических частиц также было областью исследования над прошлыми летами^38-42. Однако вся работа была выполнена по заселу сферических частиц в цилиндрических трубках. Данных о сферических частицах, осехательных в вязко-вязкостичных жидкостях между параллельными стенками, нет.

Эта работа пытается экспериментально изучить заселения сфер в стрижке истончение вязко-вязко-вязких жидкостей. Целью этого экспериментального исследования является понимание влияния эластичности жидкости, истончения и ограничение стенок на оседаемость скорости сферических частиц в истончении вязких вязко-вязких жидкостей. В настоящем документе основное внимание уделяется экспериментальным методам, используемым для этого исследования, а также некоторым репрезентативным результатам. Подробные результаты наряду с анализами можно найти в более ранней публикации⁴³.

Access restricted. Please log in or start a trial to view this content.

протокол

1. Подготовка жидкостей

Для этого экспериментального исследования используется система жидкости на основе полимера, вискоэластическая, двухкомпонентная, основанная на сурфактанте. Эта система жидкости была использована в нефтяных и газовых скважинах во многих добывающих месторождениях для^{гидроразрыва пласта 44,45}. Эта система жидкости используется для этого исследования, потому что она оптически прозрачна и реология может контролироваться путем систематического изменения концентраций и пропорций двух компонентов. Система жидкости состоит из анионического сурфактанта (например, сульфоната ксилена натрия) в качестве компонента А и катионического сурфактанта (например, N,N,N-триметила-1-октадекамония хлорида) в качестве компонента B.

1. Добавьте надлежащую концентрацию компонента А в дистиллированную воду и перемешайте при высоких об/мин с помощью накладных смесителей для обеспечения надлежащего смешивания. Дайте ему перемешать в течение 2-3 мин.
2. Добавьте в эту смесь данное концентрацию компонента В и дайте ему перемешать еще 2-3 мин.
3. Отдых смеси в течение 2-6 часов, чтобы выпустить пузырьки воздуха. Примечание: Окончательная смесь жидкости оптически прозрачна. Для этого исследования используются семь жидких смесей различных концентраций. Концентрации выбираются для получения жидкой смеси в широком диапазоне вязкостей.

2. Измерение скорости урегулирования в несыхех жидкостях

Используются стеклянные сферы диаметром от 1-5 мм.

1. Используйте микроскоп высокого разрешения для измерения диаметра стеклянных сфер. Убедитесь, что сферы имеют гладкие поверхности и являются почти идеальными сферами.
2. Храните жидкость в стеклянных контейнерах диаметром не менее 25 раз диаметром частиц, чтобы не было никакого влияния ограничивающих стенок на скорость заселения частиц.
3. Заме учет комнатной температуры и температуры жидкости с помощью лабораторного термометра. Измерение температуры важно, потому что реологические измерения жидкости должны быть сделаны при температуре, при которой проводится эксперимент по урегулированию.
4. Поместите метровую палку рядом с контейнером.
5. Аккуратно погрузите стеклянную частицу в жидкость и дайте ей осесть. Замехать процесс урегулирования с помощью видеокамеры высокого разрешения.
6. Отслеживайте положение частицы в разное время шагами от записанного видео с помощью приложения для анализа изображений. Примечание: В этой работе используется программное приложение под названием 'Tracker'(http://www.cabrillo.edu/~dbrown/tracker/).
7. Участок вертикальное положение частицы по отношению к времени и рассчитать скорость урегулирования терминала со склона линии.
8. Повторите эксперимент в рамках уникального набора условий по крайней мере 3x для обеспечения воспроизводимости. Выполните анализ изображения для различных измерений и сообщите о скорости заселения для данного диаметра частиц в определенной жидкости с помощью баров ошибок.
9. Повторите вышеуказанные шаги для частиц разного диаметра и замитмите скорость заселения. Участок урегулирования скорости по сравнению с диаметром частиц. Примечание: Рисунок 1 показывает скорость заселения пяти частиц разного размера в одной жидкости.

3. Измерение скорости заселения жидкостями между параллельными стенами

Для измерения оседаемых скоростей в присутствии параллельных стен используются две экспериментальные клетки из плексигласа.

1. При проектировании и строительстве ячейки убедитесь, что стены гладкие и идеально параллельны друг другу. Держите соотношение сторон клеток низким, чтобы убедиться, что нет никакого эффекта стен ортогональных параллельных стен. Примечание: Зазор между стенами в двух клетках в этом исследовании составляет 3,6 мм и 8 мм, соответственно. На рисунке 2 показана схема одной экспериментальной ячейки.
2. Заполните ячейку жидкостью и аккуратно отпустите частицу в клетку через вход/выходной порт. Запечатайте вход/выходной порт резиновой пробкой и позвольте частице осесть, пока она не достигнет середины клетки.
3. В этот момент тщательно распоить клетку вертикально и позволить частице осесть.
4. Поместите метровую палку рядом с ячейкой и замитмите оседают с помощью видеокамеры высокого разрешения.
5. Заме учет комнатной температуры и температуры жидкости с помощью лабораторного термометра. Это важно, потому что реологические измерения жидкости должны быть сделаны при такой температуре.
6. Как и в случае с неограниченным расчетом измерений скорости, измерять скорость урегулирования в программном приложении 'Tracker'. Повторите измерения по крайней мере три раза, чтобы обеспечить воспроизводимость и получить бары ошибок на каждом измерении.

4. Реологическая характеристика жидкостей

1. Выполните устойчивые измерения вязкости для измерения вязкости жидкости как функции скорости сласти. Примечание: В этой работе используется реометр ARES от TA Instruments с двухстенной концентрической цилиндрической арматурой (диаметр чашки: 27,95 мм, диаметр внутренней бобов: 29,50 мм, диаметр внешней бобов: 32,00 мм, внешний диаметр чашки: 34,00 мм, длина бобов: 32,00 мм).
2. Варьировать скорость стрижки от 0,1-800 сек^{-1 и} проводить измерения на уровне 10 пунктов/десятилетие. Убедитесь, что температура чашки такая же, при которой расчет эксперимент был выполнен в той же жидкости. Рисунок 3 показывает вязкость по сравнению с скоростью снора для одного образца жидкости на участке журнала.
3. Для той же жидкости вычислите диапазон скорости снора, с которым частицы сталкивались в ходе экспериментов по урегулированию. Используйте поверхность усредненой скорости движения частиц, определяемой 2V/d_p ^20,23, где V является расчетной скоростью частицы и d_p является диаметром частицы.
4. Fit кривой силового права μ-K^{n-1 в}этом диапазоне скорости стрижки на вязкости по сравнению с ставки скоута участка. На участке журнала эта пригонка будет прямой линией. Определите параметры K (индекс согласованности потока) и n (индекс поведения потока).
   K и n количественно вязкость жидкостей. На рисунке 3 показан закон о власти, подходящий на одном участке.
5. Выполните динамические измерения колебаний-стрижки в диапазоне частот от 0,1-100 рад/сек и измерьте эластичный модуль G' и вязкий модуль G''. Проймими на 10 пунктов/десятилетие.
   На рисунке 4 показаны G' и G'' для образца жидкости.
6. Вычислите соотношение двух модули, G'/G' из этих данных. Пригонка отношение модули к модели Максвелла с помощью регрессионнойанализа и вычислить время релаксации(я) жидкости. Уравнение соотношения двух модули для модели Максвелла составляет^46,47:

Время релаксации жидкости количественно эластичность жидкости. Больше времени релаксации, более эластичной является жидкость. Рисунок 5 показывает G'/G' для образца жидкости вместе с Максвелл подходят. Установка выполняется путем минимизации суммы измерения дисперсии по частоту диапазона.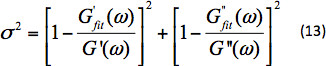

5. Определение влияния эластичности на неограниченные скорости урегулирования

1. Обозначает экспериментальную скорость заселения частицы в неограниченной жидкости V_∞VE, где '∞VE' относится к неограниченным вязко-вязко-двигательным жидкостям. Сравните эту экспериментальную скорость заселения с расчетной скоростью(V_∞INEL),рассчитанной на основе очевидных данных вязкости на основе параметров закона силы. Используйте выражения, разработанные Рено и др. ¹ для расчета V_∞INEL. Выражения упоминаются в разделе Введение. '∞INEL'относится к неограниченным неуясных жидкостей.
2. Рассчитайте соотношение V_{∞EL/V∞INEL} и обратитесь к соотношению как соотношению скорости.
   Значение соотношения скорости иллюстрирует влияние эластичности на расчетную скорость. Коэффициент скорости, более 1, предполагает увеличение скорости/снижение сопротивления из-за эластичности жидкости. Коэффициент скорости менее 1 предполагает снижение скорости/повышение сопротивления из-за эластичности жидкости.
3. Участок соотношение скорости в качестве функции диаметра частиц для различных жидкостей, чтобы наблюдать влияние эластичности на урегулирование скорости частиц разного диаметра в жидкостях различных реологий. На рисунке 6 показано соотношение скорости как функции диаметра частиц в одной из жидкостей.

6. Количественная оценка эффекта отсталости параллельных стен на скорость урегулирования

1. Рассчитайте фактор стены, F_w для данной частицы диаметра, разделив скорость заселения в присутствии параллельных стенок, V_∞VE к расчетной скорости в несыхажевой жидкости, V_∞VE.
2. Для данной жидкости, участок стены факторов, как функция диаметра частицы к стене расстояние соотношение, г. На рисунке 7 показаны факторы стены частиц, осехав в одной из жидкостей. Сюжет помогает количественно оценить эффект задержки ограничивающих стен на оседание скорости. Опустите фактор стенки, выше эффект задержки стены.

Access restricted. Please log in or start a trial to view this content.

Результаты

Эксперименты проводятся для пяти частиц разного диаметра в семи различных жидких смесях с уникальными значениями K, n и No. На рисунке 1 показана скорость заселения как функция диаметра частиц в одной жидкости. Бары ошибок показывают изменчивость в трех измерениях...

Access restricted. Please log in or start a trial to view this content.

Обсуждение

Экспериментальное исследование фокусируется на измерении скорости заселения сферических частиц в истончении вязко-вязких жидкостей в неограниченных и ограниченных условиях. Представлена подробная экспериментальная процедура получения повторяемых измерений скорости заселения. Ре...

Access restricted. Please log in or start a trial to view this content.

Материалы

Name	Company	Catalog Number	Comments
Glass Microspheres	Whitehouse Scientific	#GP1750	Available in different sieve fractions.
Rheometer	TA Instruments	ARES	Any standard rheometer capable of taking dynamic and static measurements
Anionic Surfactant (Component A)		Proprietary fluid	Used in oil field services for hydraulic fracturing. Sodium Xylene Sulfonate can be used as a substitute.
Cationic Surfactant (Component B)		Proprietary fluid	Used in oil field services for hydraulic fractuing. N,N,N-Trimethyl-1-Octadecamonium Chloride can be used as a substitute.