A buffer can prevent a sudden drop or increase in the pH of a solution after the addition of a strong acid or base up to its buffering capacity; however, such addition of a strong acid or base does result in the slight pH change of the solution. The small pH change can be calculated by determining the resulting change in the concentration of buffer components, i.e., a weak acid and its conjugate base or vice versa. The concentrations obtained using these stoichiometric calculations can be used to determine the solution’s final pH using the Henderson-Hasselbalch equation or an ICE table.

For example, a buffered solution contains 0.65 mol of formic acid and sodium formate. As the concentration of the weak acid and its conjugate base is the same here, the solution’s pH is equal to the pK_a of the weak acid, which is 3.74 in this case. If 0.05 mol HNO₃ is added into this solution, the resultant changes in the concentration of the formic acid and sodium formate can be determined by stoichiometric calculations as shown in the table below.

	H+ (aq)	HCOO− (aq)	HCOOH (aq)
Before addition (M)	~0.00 mol	0.65 mol	0.65 mol
Addition (M)	0.050 mol	-	-
After addition (M)	~0.00 mol	0.60 mol	0.70 mol

The solution’s final pH can then be determined by plugging in changed concentrations of formic acid and sodium formate into the Henderson-Hasselbalch equation.

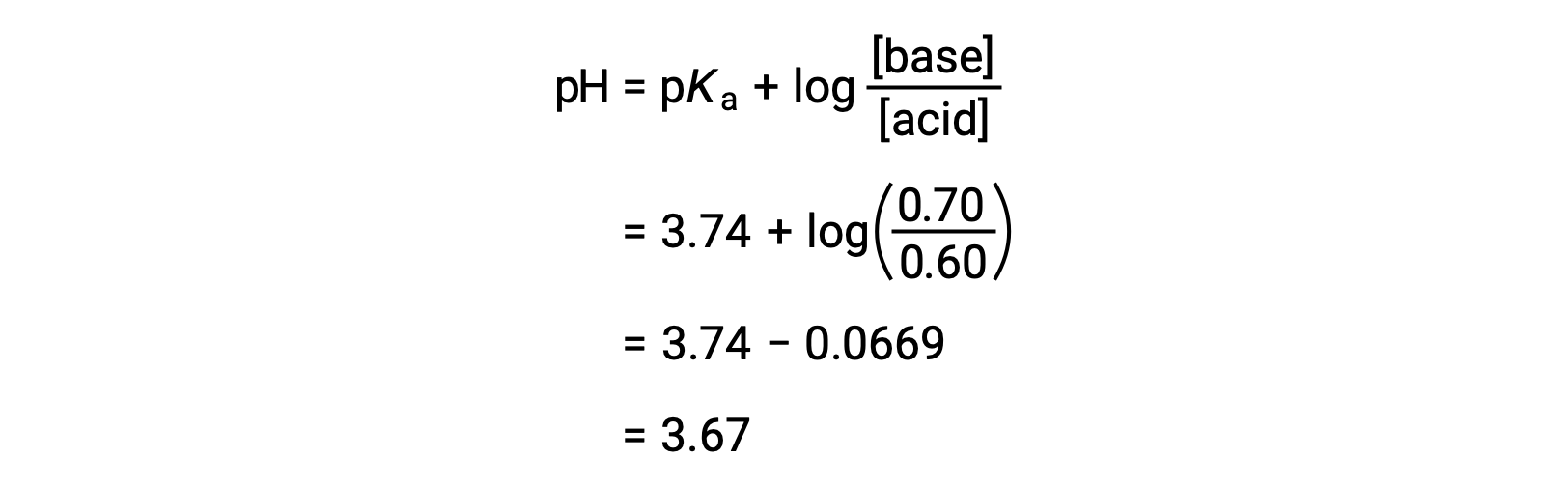
Thus, the addition of 0.05 mol of HNO₃ reduces the pH of the solution from 3.74 to 3.67.

Similarly, if 0.10 mol NaOH is added into the same solution, the resultant changes in the concentration of the formic acid and sodium formate can be determined by stoichiometric calculations as shown in the table below.

	OH− (aq)	HCOOH (aq)	HCOO− (aq)	H2O (l)
Before addition (M)	~0.00 mol	0.65 mol	0.65 mol	-­
Addition (M)	0.10 mol	-	-	­-
After addition (M)	~0.00 mol	0.55 mol	0.75 mol	­-

The final pH of the solution can then be determined by plugging in changed concentrations of formic acid and sodium formate into the Henderson-Hasselbalch equation.

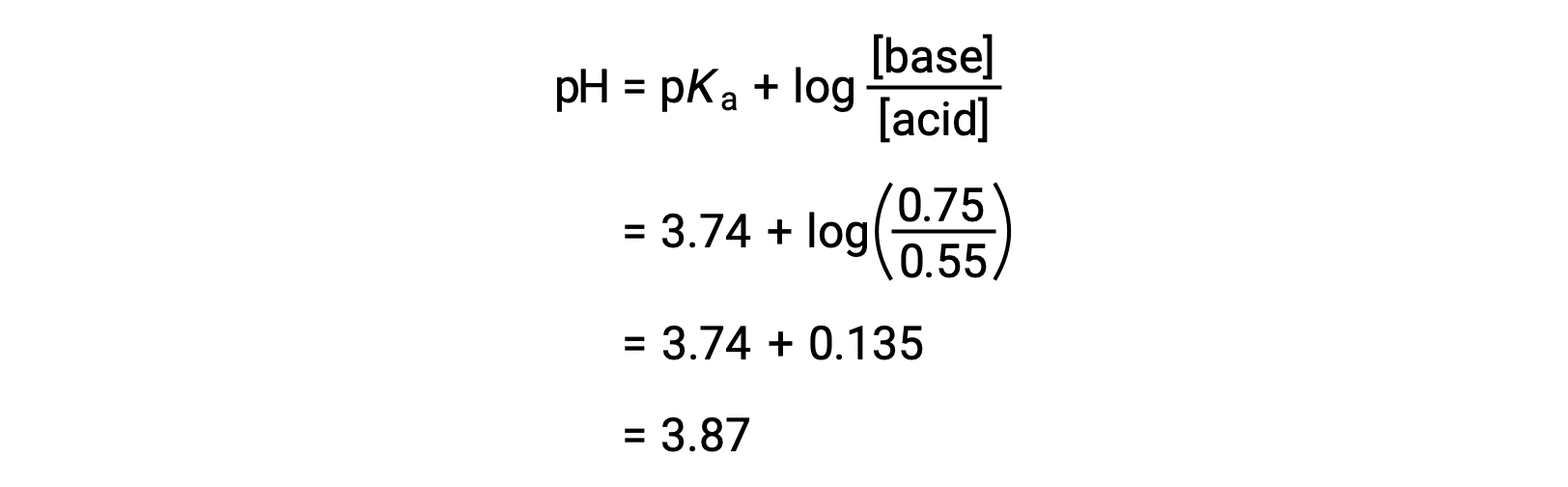
Thus, the addition of 0.10 mol NaOH increases the pH of the solution from 3.74 to 3.87.