15.1 : Simple Harmonic Motion
Simple harmonic motion is the name given to oscillatory motion for a system where the net force can be described by Hooke's law. If the net force can be described by Hooke's law and there is no damping (by friction or other non-conservative forces), then a simple harmonic oscillator will oscillate with equal displacement on either side of the equilibrium position. To derive an equation for period and frequency, the equation of motion is used. The period of a simple harmonic oscillator is given by
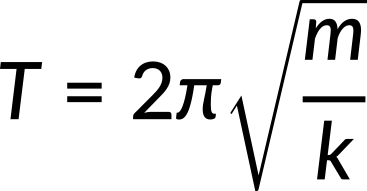
and, because the frequency and period have inverse relation, the frequency of a simple harmonic oscillator is
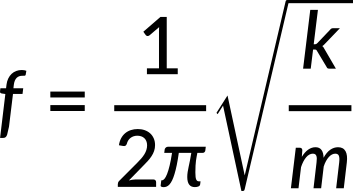
Note that neither period nor frequency has any dependence on amplitude, and the SI unit for frequency is Hertz.
Now, consider one example of each. (a) A medical imaging device produces ultrasound by oscillating with a period of 0.400 μs. What is the frequency of this oscillation? (b) The frequency of middle C on a typical musical instrument is 264 Hz. What is the time for one complete oscillation?
Both can be answered using the inverse relationship between period and frequency. Substituting the given value of period in the frequency expression, the frequency of oscillation is found.
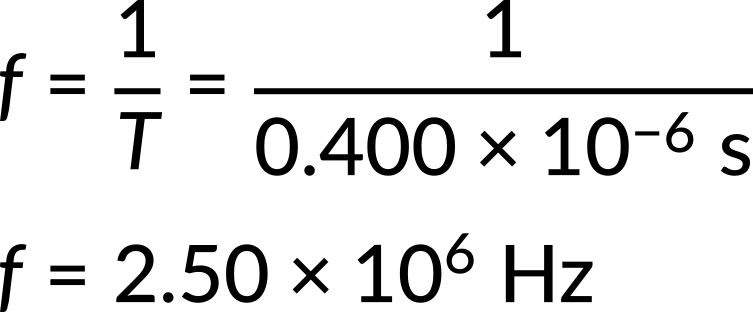
Substituting the given value for the frequency into the time period expression, the time for one complete oscillation is obtained.
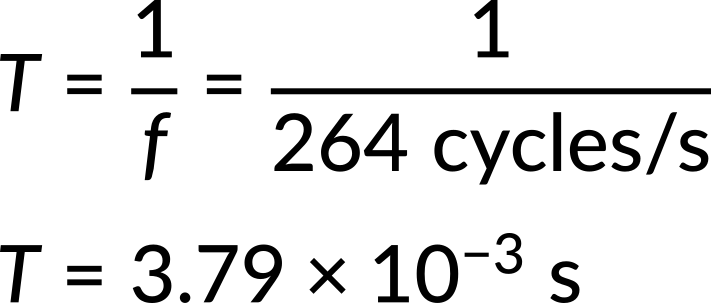
From Chapter 15:

Now Playing
15.1 : Simple Harmonic Motion
Oscillations
9.2K Views

15.2 : Characteristics of Simple Harmonic Motion
Oscillations
12.4K Views

15.3 : Oscillations about an Equilibrium Position
Oscillations
5.2K Views

15.4 : Energy in Simple Harmonic Motion
Oscillations
8.7K Views

15.5 : Frequency of Spring-Mass System
Oscillations
5.3K Views

15.6 : Simple Harmonic Motion and Uniform Circular Motion
Oscillations
4.1K Views

15.7 : Problem Solving: Energy in Simple Harmonic Motion
Oscillations
1.2K Views

15.8 : Simple Pendulum
Oscillations
4.5K Views

15.9 : Torsional Pendulum
Oscillations
5.3K Views

15.10 : Physical Pendulum
Oscillations
1.6K Views

15.11 : Measuring Acceleration Due to Gravity
Oscillations
497 Views

15.12 : Damped Oscillations
Oscillations
5.6K Views

15.13 : Types of Damping
Oscillations
6.3K Views

15.14 : Forced Oscillations
Oscillations
6.5K Views

15.15 : Concept of Resonance and its Characteristics
Oscillations
5.0K Views
Copyright © 2025 MyJoVE Corporation. All rights reserved