يمكن كتابة تعبير ثابت التأين لمحلول حمض ضعيف على النحو التالي:

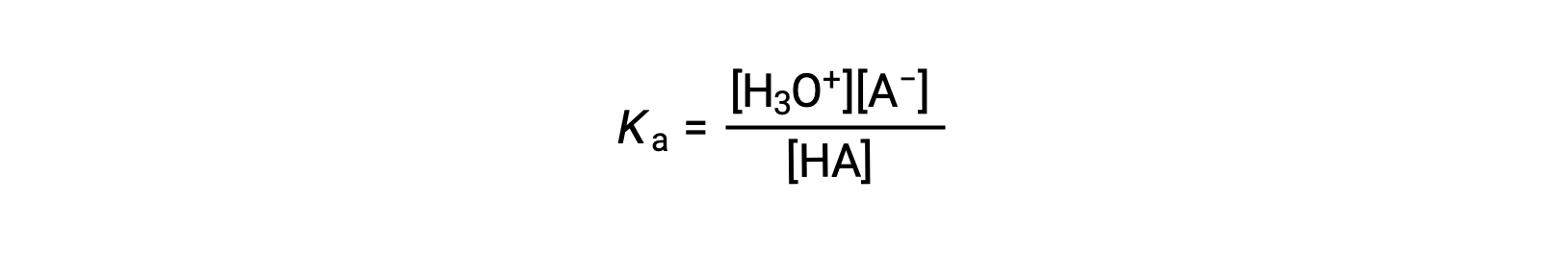
إعادة الترتيب لمحول من أجل [H₃O⁺] عوائد:

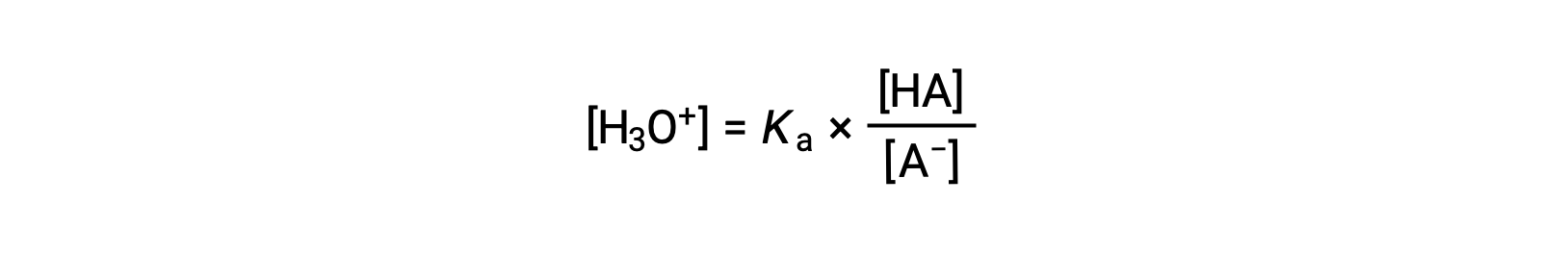
نحصل على اللوغاريتم السالب لطرفي هذه المعادلة

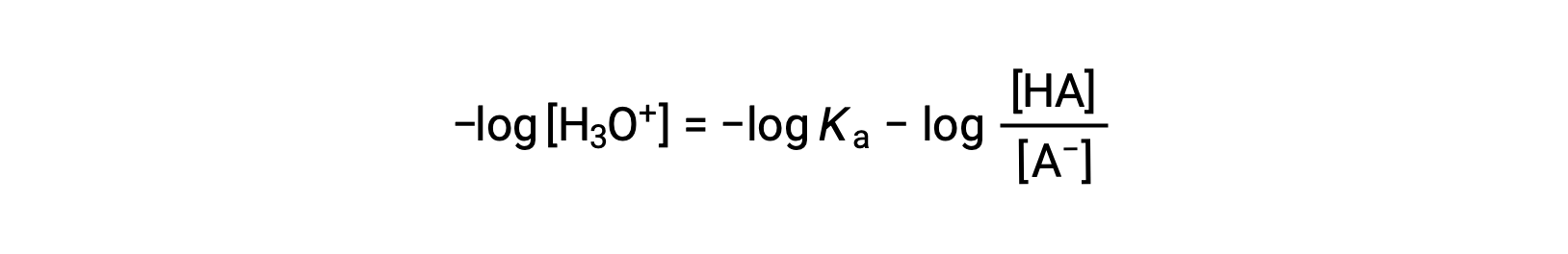
والتي يمكن كتابتها كـ

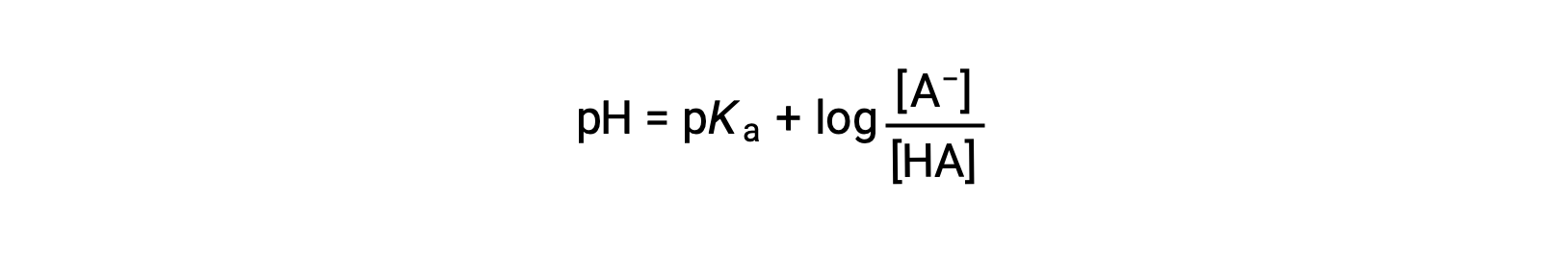
حيث pK_a هو سالب لوغاريتم ثابت التأين للحمض الضعيف (pK_a = −log K_a). تتعلق هذه المعادلة بالرقم الهيدروجيني (pH)، وثابت التأين لحمض ضعيف، وتركيزات زوج حمض-قاعدة مترافق ضعيف في محلول مخزون. غالباً ما يستخدم العلماء هذا التعبير، المسمى معادلة هندرسون-هاسلبالخ، لحساب الرقم الهيدروجيني للمحاليل المنظّمة. من المهم ملاحظة أن علامة“x هي صغيرة” يجب أن يكون الافتراض صالحاً لاستخدام هذه المعادلة.

لورانس جوزيف هندرسون وكارل ألبرت هاسلبالخ

كان لورنس جوزيف هندرسون (1878–1942) طبيباً وعالماً في الكيمياء الحيوية وعالماً فيزيولوجياً أمريكياً، على سبيل المثال لا الحصر من مساعيه العديدة. حصل على شهادة الطب من جامعة هارفارد، ثم أمضى عامين في الدراسة في ستراسبورغ، ثم جزء من ألمانيا، قبل أن يعود إلى منصب محاضر في جامعة هارفارد. أصبح في النهاية أستاذاً في جامعة هارفارد وعمل هناك طوال حياته. اكتشف أن توازن حمض-قاعدة في دم الإنسان ينظمه محلول منظّم يتكون من ثاني أكسيد الكربون المذاب في الدم. كتب معادلة في عام 1908 لوصف المحلول المنظّم لحمض الكربونيك-كربونات في الدم. كان هندرسون واسع المعرفة. بالإضافة إلى أبحاثه المهمة في فسيولوجيا الدم، فقد كتب أيضاً عن تكيفات الكائنات الحية وتناسبها مع بيئاتها وعلم الاجتماع والتعليم الجامعي. كما أسس مختبر التعب في كلية هارفارد للأعمال ، والذي فحص فسيولوجيا الإنسان مع التركيز بشكل خاص على العمل في الصناعة والتمارين الرياضية والتغذية.

في عام 1916 ، شارك الطبيب والكيميائي الدنماركي كارل ألبرت هاسيلبالخ (1874–1962) في تأليف بحث مع كريستيان بور عام 1904 وصف تأثير بوهر، والذي أظهر أن قدرة الهيموجلوبين في الدم على الارتباط بالأكسجين هي قدرة مرتبطة عكسياً بحموضة الدم وتركيز ثاني أكسيد الكربون. تم تقديم مقياس الأس الهيدروجيني في عام 1909 من قبل دانماركي آخر، س.øرينسين، وفي عام 1912، نشر هاسيلبالخ قياسات لدرجة الحموضة في الدم. في عام 1916، عبر هاسيلبالخ عن معادلة هندرسون بمصطلحات لوغاريتمية، بما يتفق مع المقياس اللوغاريتمي للأس الهيدروجيني، وبالتالي ولدت معادلة هندرسون-هاسلبالخ.

هذا النص مقتبس من Openstax, Chemistry 2e, Section 14.6: Buffers.