光子纳米结构的光谱和角度解析磁-光学特性

摘要

光子带结构有助于了解闭用电磁模式如何在光子晶体中传播。在包含磁性元件的光子晶体中，这种闭锁和共振光学模式伴随着增强和修饰的磁光活性。我们描述了一个测量过程，通过傅立叶空间显微镜提取磁光带结构。

摘要

光子晶体是周期性纳米结构，可以支持各种闭塞电磁模式。这种封闭模式通常伴随着局部增强的电场强度，从而加强光物质相互作用，从而实现表面增强拉曼散射（SERS）和表面质子增强传感等应用。在存在磁光活性材料的情况下，局部场增强产生异常磁光活性。通常，给定光子晶体的闭合模式在很大程度上取决于入射电磁辐射的波长和入射角。因此，需要光谱和角分辨率测量来完全识别它们，并建立它们与晶体的磁光活性的关系。在本文中，我们将介绍如何使用傅立叶平面（后焦平面）显微镜来描述磁光学活性样品。作为一个模型系统，我们在这里使用由磁光有源Au/Co/Au多层构建的质子光栅。在实验中，我们在原位对光栅施加磁场，并测量其对等空间响应，获得光栅在波长和事件角度范围内的磁光响应。这些信息使我们能够建立光栅的质子带结构以及角度和波长相关磁光活性的完整图谱。这两幅图像使我们能够精确定位质子共振对光栅的磁光反应的影响。磁光效应相对较小，需要对采集的光信号进行仔细处理。为此，提出了从采集的原始数据获取磁光响应的图像处理协议。

引言

光子晶体中的封闭电磁模式可能来自各种不同的起源，例如金属/电接口周围的等离子体共振或高折射率介电纳米^{结构1、2、3}中的Mie共振，并可设计为以特定定义^{的频率4、5}出现。它们的存在产生了许多迷人的现象，如光子带间隙6，7，8，强光子^定位9，慢^光10和狄拉克^锥11。傅立叶平面显微镜和光谱学是光子纳米结构表征的基本工具，因为它们能够捕获其中发生的封闭模式的许多基本特性。在傅立叶空间显微镜中，与传统的真实平面成像相比，信息以角^{坐标12、13}的函数的形式呈现。它也被称为后焦平面（BFP）成像，因为从显微镜物镜的后焦平面记录出样品发出的光的角分解。角光谱，即样品的远场发射模式与从它发出的光动量（[k] ） 相关。特别是，它代表其平面内动量 （k_x，k_y）分布¹⁴。

在磁光有源样品中，有密闭的光子激发的存在，可以大大增强磁光响应15、16、17、18、19。磁光效应取决于磁场和事件电磁辐射的相互几何形状。图1中描述了线性偏振光及其命名法中最常遇到的磁光几何形状。在这里，我们演示了一个设置，可用于探索在反射中观察到的两种磁光效应:横向和纵向磁光克尔效应，分别缩写为TMOKE和LMOKE。TMOKE 是一种强度效应，其中相对磁化状态的反射度不同，而 LMOKE 表现为反射光极化轴的旋转。其效果由磁化相对于光入射的方向来区分，对于LMOKE，磁化与光波矢量的平面内分量平行，而对于TMOKE，则与它相平行。对于通常的射像光，光动量的平面内分量均为空（k_x = k_y = 0），因此，两个效应均为零。可以很容易地设想出同时存在这两种效应的配置。但是，为了简化数据分析，在本演示中，我们仅限于仅存在一种影响的情况，即 TMOKE。

多种光学配置可用于测量磁光子晶体发出的光的角分布。例如，在Kalish^等人20和博罗夫科娃^等人21，这种设置成功地用于传输几何，以揭示质子对磁光现象的影响。例如，在Kurvits^等人22中，为使用无穷大校正物镜的显微镜提供了一些可能的配置。在图 2A所示的配置中，我们使用无穷大校正透镜，其中来自样本中给定点的光由物镜定向到共线光束中。在图 2A中 ，从顶部（虚线）和样本底部（实线）出现的光束进行了图式描述。然后，使用收集镜头对这些光束重新聚焦，以在图像平面 （IP） 上形成图像。第二个透镜，也称为 Bertrand 透镜，然后放置在图像平面之后，将焦平面上的入射光分离成角度组件，如图 2A所示，红色、蓝色和黑色。从这个后焦平面，样品发出的光的角度分布可以通过相机测量。实际上，贝特朗镜头对到达它的光束执行傅立叶变换。BFP 的空间强度分布对应于事件辐射的角分布。通过用与收集样品响应相同的目标照亮样品，可以建立样品的完全倒数空间反射图。传入和流出的光束使用分束器进行分离。完整的设置如图3A 所示。为了获得光谱，需要可调光源或单色器。然后，测量可以在不同的波长上重复，请记住，由于标准光源的光谱，结果需要归一化为控制样品的反射率。为此，可以使用镜像或已特意未图案的样本的一部分，以允许高反射率。为了协助定位，我们展示了如何将设置与额外的光学系统集成，从而对样品进行实时空间成像，如图2B所示。

我们现在着手建立一种测量光子晶体角解磁光光谱的方法，使用作为代表性样品的DVD光栅覆盖在Au/Co/Au薄膜上，其中铁磁钴的存在引起相当大的磁光^活性23。DVD 光栅的周期性波纹使表面质子极性子 （SPP） 共振在不同波长角组合下，由

其中n是周围环境的折射率，k₀是自由空间中光的波向量，±₀是入射角，d是光栅的周期性，m是表示 SPP 顺序的整数。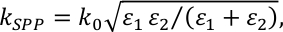 SPP波向量由+1和+2是金属层和周围介电环境的允许性。由于金/钴多层薄膜的厚度，我们可以假设SSP只在多层薄膜上激发。

研究方案

1. 安装设置

1. 光学
   注: 在具有足够振动隔离的光学表上构建如图 3A所示的设置。为了避免球面和其他畸变，请将所有光学元件（透镜、针孔等）与光束聚焦。光学布置如图2所示，其中显示了元件之间的距离。
   1. 将光从白色光源引导到单色器，以获得单色光束。有关此工作中使用的设置的详细信息，请参阅材料表。将单色器设置为具有良好强度和可见性的波长，例如 550 nm。光谱可见部分的波长使得定位光学元件更加容易。
   2. 使用耦合透镜，将光耦合到光纤上，并将其与光纤端端的物镜进行连接。根据所使用的光源，可以省略此步骤。
   3. 将偏振器从准直透镜放置 250 mm，以线性偏振光束，并将一个分束器从偏振器中放置 100 mm，以将光线引导至显微镜物镜。
      注:由于可准化光束，上述组件的指定位置不会影响测量设置的光学元件，仅供参考。
   4. 将样品放在样品支架上，该样品带有 x-y-z 平移级和旋转级，使样品围绕 z 轴进行 360 度旋转，即光线轴冲击样品。
   5. 将目标镜头安装在平移台上，实现三个方向的运动。其中最关键的是聚焦到样品所需的 z 轴。
      注:样品翻译所需的设备取决于所使用的样品。大型同质样品可以手动定位，而有用面积小的样品需要更仔细的定位，尤其是在使用针孔限制成像区域时（步骤 1.1.7.）。从样品中冒出的光束的光学元件如图 2 所示。无限校正的物镜将波前从样品的每个点变成共线光束。
   6. 将带 f = 200 mm（管透镜）的收集器镜头放置在距目标 330 mm 的位置，以重新聚焦光束以在图像平面上形成图像。由于样品发出的光的共线性传播，收集器镜头可以放置在与物镜的任何距离。
      注: 与之前一样，从物镜中产生的光是准直的。但是，管透镜应放在分束器之后。
   7. 将针孔放置在距收集器镜头 200 mm 的图像平面中，以将图像区域限制为图案区域。将针孔放在梁的中心。如果使用针孔，请使用样本的真实空间图像来定位它。对于图案区域大于光束照亮的区域的样本，则不需要这样做。
   8. 将第二个镜头置于 f = 75 mm（贝特朗镜头）后 120 mm 的图像平面上，以创建图像角度分量的傅立叶变换。变换在第二个镜头的聚焦处创建，并带有一个科学的sCMOS摄像机，该摄像机距离贝特朗镜头75毫米。
   9. 仅对于 LMOKE 测量，在分束器和收集器镜头之间插入一个与第一个偏振器的角度为重定度的附加偏振器。
2. 磁铁
   1. 将磁铁连接到电源并安装，以便磁场可以施加在样品上。选择磁场是应用于纵向、横向还是极性方向（图1）。
3. 样品制备
   1. 机械拆除商业DVD磁盘;随后，暴露的光栅表面由于其衍射性特性而易于识别。使用胶带剥离以前的涂层。清洁表面，将其浸泡在乙醇中 10 分钟。光栅现在已准备好接收磁质涂层。
      注:不同的商业光盘（如蓝光和 CD）可能需要不同的制备协议。
   2. 通过电子束蒸发将金属薄膜沉积在裸露的光栅上。为确保低粗糙度，请使用小于 5 °/s 的蒸发率。
   3. 从 4 nm Cr 粘接层开始，沉积交替的黄金和钴层，用金封层进行精加工，以确保防止氧化。
      注: 我们使用以下数量的层和厚度: Cr （4 nm）/Au （16 nm）/[Co （14 nm）/Au （16 nm）] = 4/Co （14 nm）/Au （7 nm）。
   4. 执行光学或电子显微镜（图4A）以验证样品表面条件，以防均匀性和低缺陷继续测量。

2. 测量程序

1. 样品定位
   注:作为示例，我们将测量覆盖磁质Au/Co/Au薄膜的DVD光栅。由于光栅的周期性波纹，PSP 可以根据波前波长在特定入射角度激发。
   1. 使用一小滴银漆将样品安装在样品架上。让银漆干燥10分钟。
   2. 在图像平面后插入翻转镜，以便对样本进行真实空间成像。插入 f = 125 mm 的镜头 L1，使图像平面处于对焦位置，并将 F = 250 mm 置于距 L1 135 mm 的 L2 位置。
   3. 最后，将电荷耦合器件（CCD）摄像机从L2放置210mm，以捕捉图像平面的放大图像。移动镜头 L1 和 L2，直到将针孔放置在图像平面上，使相机对焦。
   4. 将物镜朝样品移动，直到样品在 CCD 相机中处于良好对焦。
2. 光学反射率测量
   1. 使用样品的真实空间图像，将光斑放置在样品的反射（未图案）部分。翻转翻转镜以查看显微镜的 BFP。
      注:在这里，对于 DVD 光栅，我们使用 DVD 磁盘边缘的连续金属薄膜。
   2. 选择与所需极化状态相对应的后焦平面区域。极化和后焦平面位置之间的关系如图3B所示。沿对应于 TM 极化的轴选择感兴趣区域 （AOI） 作为目标后焦平面的矩形横截面（图 3C中的蓝色矩形）。
      注:在本手稿中使用的仪器软件中，这是通过使用光标选择器选择 AOI 来实现的。然后，软件沿矩形的短尺寸对强度进行平均，并将生成的频谱视为一个 1D 数据数组，其中每个数据点对应于样本的不同发射角度。在质子光栅中，只有TM极化光，即与光栅槽垂直的电场的EM辐射才能激发质子共振。因此，根据光栅方向，有必要选择正确的极化状态，选择 BFP 的垂直或水平切片。
   3. 通过单击"测量规范化光谱"来测量光源的光谱，稍后将用它来规范化测量的反射率数据。由于每个波长产生一组 1D 数据点，光源的全谱被保存为 2D 张量，其中每个数据点表示波长和角度的组合。
   4. 再次使用样品的真实空间图像，将光源放置在感兴趣的光子晶体上。切换回 BFP 时，确保质子模式作为穿过后焦平面的暗线可见。当入射光的波长被修改时，线条会移动。
   5. 使用相同的AOI和测量设置（即曝光时间、平均值），通过单击"测量反射光谱"测量光子晶体的反射光谱。
   6. 为了考虑光源强度的光谱变化，通过光源的光谱对得到的光谱进行标准化。这将生成从 0 到 1 的 2D 数字数组，其中 1 对应于完全反射，0 对应于完全吸收条件。
3. 磁光测量
   1. 通过使用已知对应于良好磁光响应的角度和波长测量迟滞回路，开始磁光测量，通常这些条件可以接近 SPP 激发。为此，请选择 SPP 激发附近的小 AOI 并测量单个环路。
      注:量化磁光活性所需的数据分析取决于样品所展示的磁力类型。在这里，我们假设一个铁磁反应，并相应地处理结果。磁或顺磁响应本质上是与应用磁场的线性响应，可以量化为每个应用磁场单元的光性能变化。铁磁性材料表现出非线性的允许性，在定义磁光响应时需要额外的考虑（参见图3D）。TMOKE被定义为反射强度的变化，即应用磁场的函数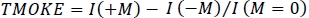，即，I（M）是样品在磁化状态M下反射的强度。
   2. 使用 2.3.1 中测量的滞后回路，选择要循环的磁场范围。对于铁磁样品，将磁场从完全饱和状态循环到相反的饱和状态，从而在饱和场上舒适地扩展范围。稍后，使用在饱和状态下测量的点来分析和移除任何可以通过线性贡献验证的硅磁或顺磁贡献。
   3. 最后，测量样品在定义的每个磁场点上反射的强度，如果需要，在多个环路上重复。每个波长和磁化点产生单个一维数值数据数组（即测量的光强度），其中阵列的每个点对应于特定角度。

3. 数据分析

1. 使用步骤 2.3.1 中测量的样本的滞后回路，分配步骤 2.3.3 中测量的每个帧。到饱和状态或中间状态（图3C）。
2. 放弃中间帧，从测量的强度中计算磁光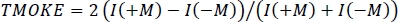活动，其中每个角度和波长数据点分别执行操作。
   注:由于 TMOKE 表示为相对强度变化，因此结果不必归一化为灯谱。
3. 如果样本显示大顺磁（或更罕见地，反磁）活动，需要减去饱和磁状态之间的可靠比较，则通过拟合在饱和度测量的点上（同样，每个角度和波长点以像素为单位）线，并移除线性贡献。

结果

图 4A显示了一个带有 Au/Co/Au 多层覆盖的商业 DVD 光栅的扫描电子显微镜 （SEM） 显微图，该微光图在我们的实验中使用了演示样本。其光学光谱和磁光光谱分别如图4B，C所示。 有关样品制造详情的详情载于^{其他部分23。}图4A，B中的黑线显示了从方程1计算的质子分散关系。Au/C...

讨论

我们引入了测量设置和协议，以获得光学晶体的角解析磁光光谱。特别是，对铁磁性材料的情况进行了阐述，它需要额外的数据分析，以考虑材料的非线性渗透性。与非角解析方法（在光学和磁光光谱中显示为明确定义的频段）时，角解析磁光光谱具有额外的优势，即闭合模式可以更容易识别。我们在这里展示的方法可以很容易地适应各种光子晶体，并不限于表面质子共振。

材料

Name	Company	Catalog Number	Comments
Beam splitter	Thorlabs	BSW27
Bertrand lens	Thorlabs	LA1608	f = 75 mm
CCD Camera	Thorlabs	1500M-GE-TE	Camera for real space imaging
Collecting lens	Thorlabs	ITL200	f = 200 mm
Collimating lens	Zeiss	420640-9800	Magnification 10x NA 0.3
Flip mirror	Thorlabs	CCM1-P01/M
Flip mirror mount	Thorlabs	FM90/M
L1-lens	Thorlabs	LA1986	f = 125 mm
L2-lens	Thorlabs	LA1461	f = 250 mm
Objective lens	Nikon	MUE10500	Magnification 50x NA 0.8
Pinhole	Thorlabs	ID8/M
Polarizer	Thorlabs	GTH10M	For LMOKE measurements, two polarizers are needed
sCMOS camera	Andor	ZYLA-4.2P-USB3