Spectral and Angle-Resolved Magneto-Optical Characterization of Photonic Nanostructures

Summary

Photonic band structure enables understanding how confined electromagnetic modes propagate within a photonic crystal. In photonic crystals that incorporate magnetic elements, such confined and resonant optical modes are accompanied by enhanced and modified magneto-optical activity. We describe a measurement procedure to extract the magneto-optical band structure by Fourier space microscopy.

Abstract

Photonic crystals are periodic nanostructures that can support a variety of confined electromagnetic modes. Such confined modes are usually accompanied by local enhancement of electric field intensity that strengthens light-matter interactions, enabling applications such as surface-enhanced Raman scattering (SERS) and surface plasmon enhanced sensing. In the presence of magneto-optically active materials, the local field enhancement gives rise to anomalous magneto-optical activity. Typically, the confined modes of a given photonic crystal depend strongly on the wavelength and incidence angle of the incident electromagnetic radiation. Thus, spectral and angular-resolved measurements are needed to fully identify them as well as to establish their relationship with the magneto-optical activity of the crystal. In this article, we describe how to use a Fourier-plane (back focal plane) microscope to characterize magneto-optically active samples. As a model system, here we use a plasmonic grating built out of magneto-optically active Au/Co/Au multilayer. In the experiments, we apply a magnetic field on the grating in situ and measure its reciprocal space response, obtaining the magneto-optical response of the grating over a range of wavelengths and incident angles. This information enables us to build a complete map of the plasmonic band structure of the grating and the angle and wavelength dependent magneto-optical activity. These two images allow us to pinpoint the effect that the plasmon resonances have on the magneto-optical response of the grating. The relatively small magnitude of magneto-optical effects requires a careful treatment of the acquired optical signals. To this end, an image processing protocol for obtaining magneto-optical response from the acquired raw data is laid out.

Introduction

Confined electromagnetic modes in photonic crystals can arise from a variety of different origins, such as plasmon resonances around metal/dielectric interfaces or Mie resonances in high refractive index dielectric nanostructures^1,2,3, and can be designed to appear at specifically defined frequencies^4,5. Their presence gives rise to many fascinating phenomena such as photonic band gaps^6,7,8, strong photon localization⁹, slow light¹⁰ and Dirac cones¹¹. Fourier plane microscopy and spectroscopy are basic tools for characterization of photonic nanostructures as they enable capturing many essential properties of confined modes occurring in them. In Fourier space microscopy, as opposed to conventional real plane imaging, the information is presented as the function of angular coordinates^12,13. It is alternatively known as back focal plane (BFP) imaging as the angular decomposition of the light emanating from the sample is recorded from the back focal plane of the microscope objective. The angular spectrum, i.e., the far field emission pattern of the sample is related to the momentum of light emanating from it (ħk). In particular, it represents its in-plane momentum (k_x,k_y) distribution¹⁴.

In magneto-optically active samples, the presence of confined photonic excitations has been shown to result in considerable enhancement of the magneto-optical response^{15,16,17,18,19}. Magneto-optical effects depend on the mutual geometry of the magnetic field and the incident electromagnetic radiation. Most commonly encountered magneto-optical geometries for linearly polarized light and their nomenclature are depicted in Figure 1. Here, we demonstrate a setup that can be used to explore two magneto-optical effects that are observed in reflection: transverse and longitudinal magneto-optical Kerr effects, abbreviated, respectively, as TMOKE and LMOKE. TMOKE is an intensity effect, where the reflectivities of the opposing magnetization states are different while LMOKE manifests as a rotation of the reflected light polarization axis. The effects are distinguished by the orientation of the magnetization with respect to the light incidence, where for LMOKE, the magnetization is oriented parallel to the in plane component of the wave vector of the light while for TMOKE it is transverse to it. For normally incident light, both in-plane components of the momentum of light are null (k_x = k_y = 0) and, consequently, both effects are zero. Configurations where both effects are present can be easily conceived. However, to simplify the data analysis, in this demonstration we limit ourselves to situations where only one of the effects is present, namely TMOKE.

Several optical configurations can be used to measure the angular distribution of light emitted from magnetophotonic crystals. For example, in Kalish et al.²⁰ and Borovkova et al.²¹, such a setup was successfully used in transmission geometry to unveil plasmon influence on magneto-optical phenomena. As an illustration, in Kurvits et al.²², some possible configurations are presented for a microscope that uses an infinity corrected objective lens. In our configuration, depicted in Figure 2A, we use an infinity corrected lens where the light coming from a given point in the sample is directed by the objective lens into collinear beams. In Figure 2A, beams emerging from the top (dashed lines) and the bottom (solid lines) of the sample are schematically depicted. Then, a collecting lens is used to refocus these beams to form an image at the image plane (IP). A second lens, also known as Bertrand lens, is then placed after the image plane to separate the incoming light at its focal plane into angular components, depicted in Figure 2A in red, blue and black. From this back focal plane, the angular distribution of the light emitted by the sample can be measured with a camera. Effectively, the Bertrand lens performs a Fourier transform on the light beam arriving at it. The spatial intensity distribution at the BFP corresponds to the angular distribution of the incident radiation. A full reciprocal space reflectance map of the sample can be established by illuminating the sample with the same objective that is used to collect the response of the sample. The incoming and out going beams are separated using a beam splitter. The complete setup is depicted in Figure 3A. To obtain a spectrum, a tunable light source or a monochromator is needed. The measurement can then be repeated over different wavelengths, keeping in mind that due to the spectrum of standard light sources, the results need to be normalized to the reflectivity of a control sample. For this purpose, one can use a mirror or a part of the sample that has been purposefully left unpatterned to allow for a high reflectivity. To assist in positioning, we show how to integrate the setup with an additional optical system that enables real-space imaging of the sample, shown in Figure 2B.

We now proceed to establish a method for measuring the angular resolved magneto-optical spectrum of a photonic crystal, using as a representative sample, a DVD grating covered with an Au/Co/Au film where the presence of ferromagnetic cobalt gives rise to considerable magneto-optical activity²³. The periodic corrugation of the DVD grating enables surface plasmon polariton (SPP) resonances at distinct wavelength-angle combinations that are given by

where n is the refractive index of the surrounding environment, k₀ the wave vector of light in free space, θ₀ the incidence angle, d the periodicity of the grating and m is an integer denoting the order of the SPP. The SPP wave vector is given by 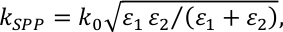where ε₁ and ε₂ are the permittivities of the metallic layer and the surrounding dielectric environment. Due to the thickness of the gold/cobalt multilayer film, we can assume that SPPs are only excited on top of the multilayer film.

Protocol

1. Mounting the setup

1. Optics
   NOTE: Build the setup as depicted in Figure 3A on an optical table with sufficient vibration isolation. To avoid spherical and other aberrations, center all the optical components (lenses, pinholes etc.) with respect to the beam. The optical arrangement is shown in Figure 2 with the distances between components indicated.
   1. Guide the light from the white light source to a monochromator to obtain a monochromatic light beam. See the Table of Materials for details of the setup used in this work. Set the monochromator to a wavelength that has a good intensity and visibility, e.g., 550 nm. A wavelength from the visible part of the spectrum makes it easier to position the optical elements.
   2. Using a coupling lens, couple the light to a fiber and collimate it with an objective at the fiber termination. Depending on the light source used, this step may be omitted.
   3. Place a polarizer 250 mm from the collimating lens to linearly polarize the beam and place a beam splitter 100 mm from the polarizer to guide the light to the microscope objective lens.
      NOTE: Due to the collimated beam, the indicated positions of the above-mentioned components do not affect the optics of the measurement setup and are given just for guidance.
   4. Place the sample on the sample holder equipped with a x-y-z translation stage and a rotation stage that enables a 360-degree sample rotation around the z-axis, i.e., the axis of light impinging on the sample.
   5. Mount the objective lens on a translation stage that enables movement in three directions. The most crucial of these is the z-axis that is needed for focusing onto the sample.
      NOTE: The required equipment for sample translation depends on the samples used. Large, homogenous samples may be positioned manually while samples with small useful area will require more careful positioning, especially when using a pinhole to limit the imaged area (step 1.1.7.). The optics of the beam emerging from the sample is schematically depicted in Figure 2. The infinity corrected objective lens directs wave fronts emerging from each point of the sample into collinear beams.
   6. Place a collector lens with f = 200 mm (tube lens), 330 mm from the objective to re-focus the beams to form an image at the image plane. Due to the collinear propagation of the light emanating from the sample, the collector lens can be placed at any distance from the objective lens.
      NOTE: As before, the light emerging from the objective lens is collimated. However, the tube lens should be placed after the beam splitter.
   7. Place a pinhole into the image plane at 200 mm from the collector lens to limit the imaged region to the patterned area. Place the pinhole at the center of the beam. If using a pinhole, use the real space image of the sample to position it. For samples where the patterned area is larger than the area illuminated by the light beam, this is not necessary.
   8. Place a second lens with f = 75 mm (Bertrand lens), 120 mm after the image plane to create a Fourier transform of the angular components of the image. The transform is created at the focus of the second lens and imaged with a scientific sCMOS camera which is placed 75 mm from the Bertrand lens.
   9. For LMOKE measurements only, insert an additional polarizer with an angle with respect to the first polarizer between the beam splitter and the collector lens.
2. Magnet
   1. Connect the magnet to a power supply and mount it so that the magnetic field can be applied on the sample. Choose whether the magnetic field is applied in the longitudinal, transversal or polar direction (Figure 1).
3. Sample preparation
   1. Mechanically dismantle a commercial DVD disk; subsequently the exposed grating surface can be easily identified due its diffractive proprieties. Use an adhesive tape to peel the previous coatings. Clean the surface, soak it in ethanol for 10 min. The grating is now ready to receive a magneto-plasmonic coating.
      NOTE: Different commercial optical disks as Blu-ray and CDs, may need a different preparation protocol.
   2. Deposit the metal film on the exposed grating by electron-beam evaporation. To ensure low roughness, use evaporation rates smaller than 5 Å/s.
   3. Starting with a 4 nm Cr adhesive layer, deposit alternating gold and cobalt layers, finishing with a gold capping layer to ensure protection from oxidation.
      NOTE: We used the following number of layers and thicknesses: Cr (4 nm)/Au (16 nm)/[Co (14 nm)/Au (16 nm)] × 4/Co (14 nm)/Au (7 nm).
   4. Perform optical or electron microscopy (Figure 4A) to verify the sample surface conditions, in case of homogeneity and low defects proceed with the measurement.

2. Measurement procedure

1. Sample positioning
   NOTE: As an illustrative sample, we will measure a DVD grating covered with magnetoplasmonic Au/Co/Au film. Due to the periodic corrugation of the grating, SPPs can be excited at certain angles of incidence based on the wavefront wavelength.
   1. Mount the sample on the sample holder using a small drop of silver paint. Let the silver paint dry for 10 min.
   2. Insert a flip mirror after the image plane to enable real space imaging of the sample. Insert a lens L1 with f = 125 mm so that the image plane is in focus and place L2 with f = 250 mm at 135 mm distance from L1.
   3. Finally place a charge-coupled device (CCD) camera 210 mm from L2 to capture a magnified image of the image plane. Move lenses L1 and L2 until the pinhole placed in image plane in good focus on the CCD camera.
   4. Move the objective lens towards the sample until the sample is in good focus in the CCD camera.
2. Optical reflectivity measurement
   1. Using the real space image of the sample, position the light spot over a reflective (unpatterned) part of the sample. Flip the flip mirror to see the BFP of the microscope.
      NOTE: Here, for the DVD-grating we use the continuous metallic film at edge of the DVD disk.
   2. Select the area of the back focal plane that corresponds to the desired polarization state. The relationship between polarization and position in the back focal plane is shown in Figure 3B. Select an area of interest (AOI) as a rectangular cross section of the objective back focal plane (blue rectangle in Figure 3C) along the axis that corresponds to TM-polarization.
      NOTE: In the instrumentation software used in this manuscript, this is achieved by selecting the AOI using the cursor selectors. The software then averages the intensities along the short dimension of the rectangle and treats the resulting spectrum as a 1D array of data where each data point corresponds to a different emission angle of the sample. In plasmonic gratings, only TM-polarized light, i.e., EM radiation with electric field perpendicular to the grating grooves, can excite the plasmon resonances. Thus, depending on the grating orientation, it is necessary to select the correct polarization state by either choosing a vertical or horizontal slice of the BFP.
   3. Measure the spectrum of the light source by clicking Measure normalization spectrum, which will be used later to normalize the measured reflectivity data. As each wavelength yields a 1D set of data points, the full spectrum of the light source is saved as a 2D tensor where each data point represents a combination of wavelength and angle.
   4. Using again the real space image of the sample, position the light source over the photonic crystal of interest. When switching back to BFP, ensure that the plasmon modes are visible as dark lines crossing the back focal plane. The lines move as the wavelength of the incident light is modified.
   5. Using the same AOI and measurement settings (i.e., exposure times, number of averages), measure the reflection spectrum of the photonic crystal by clicking Measure reflection spectrum.
   6. To account for the spectral variation in light source intensity, normalize the obtained spectrum by the spectrum of the light source. This will yield a 2D array of numbers from 0 to 1 where 1 corresponds to fully reflective and 0 to fully absorptive conditions.
3. Magneto-optical measurement
   1. Start the magneto-optical measurement by measuring a hysteresis loop using an angle and wavelength that are known to correspond to a good magneto-optical response, usually these conditions can be found close to the SPP excitations. To do that, choose a small AOI near the SPP excitations and measure a single loop.
      NOTE: The data analysis needed to quantify the magneto-optical activity depends on the type of magnetism that the sample exhibits. Here, we assume a ferromagnetic response and treat the results accordingly. Dia- or paramagnetic response is essentially linear to applied magnetic field and can be quantified as change in optical properties per applied magnetic field unit. Ferromagnetic materials exhibit a non-linear permittivity that requires additional consideration when defining the magneto-optical response (See Figure 3D). The TMOKE is defined as change in reflected intensity as the function of applied magnetic field, i.e.,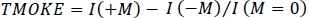 , where I(M) is the intensity reflected by the sample at magnetization state M.
   2. Using the hysteresis loop measured in 2.3.1., choose the range of magnetic fields to loop. For ferromagnetic samples, loop the fields from a fully saturated state to an oppositely saturated state, extending the range comfortably over the saturation field. Later, use the points measured in the saturated state to analyze and remove any dia- or paramagnetic contributions that can be verified by their linear contribution.
   3. Finally, measure the intensity reflected by the sample at each magnetic field point defined, repeating over multiple loops if desired. Each wavelength and magnetization point yield a single 1D array of numerical data (i.e., measured light intensity) where each point of the array corresponds to a particular angle.

3. Data analysis

1. Using the hysteresis loop of the sample measured at step 2.3.1, assign each frame measured at step 2.3.3. to either of the saturated states or to the intermediate state (Figure 3C).
2. Discard the intermediate frames and calculate the magneto-optical activity from the measured intensities by 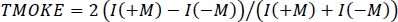, where the operations are carried out separately for each angular and wavelength data point.
   NOTE: As TMOKE is expressed as a relative intensity change, the results do not have to be normalized to the lamp spectrum.
3. If the sample presents large paramagnetic (or more rarely, diamagnetic) activity that needs to be subtracted for a reliable comparison between the saturated magnetic states, subtract the linear contribution arising from para- or diamagnetic activity by fitting a line (again, pixelwise separately for each angle and wavelength point) on the points measured at saturation and remove the linear contribution.

Results

Figure 4A shows a scanning electron microscope (SEM) micrograph of a commercial DVD grating covered with Au/Co/Au multilayer that was used a demonstration sample in our experiments. Its optical and magneto-optical spectra are shown in Figure 4B,C respectively. Details on sample fabrication are presented elsewhere²³. Black lines in Figure 4A,B show the plasmon...

Discussion

We have introduced a measurement setup and protocol to obtain angular resolved magneto-optical spectra of optical crystals. In particular, the case of ferromagnetic materials, that requires additional data analysis to account for the nonlinear permeability of the material, has been laid out. Angular resolved magneto-optical spectroscopy presents an additional advantage over non-angular resolved methods that the confined modes can be more readily identified as they appear as clearly defined bands in both optical and magne...

Materials

Name	Company	Catalog Number	Comments
Beam splitter	Thorlabs	BSW27
Bertrand lens	Thorlabs	LA1608	f = 75 mm
CCD Camera	Thorlabs	1500M-GE-TE	Camera for real space imaging
Collecting lens	Thorlabs	ITL200	f = 200 mm
Collimating lens	Zeiss	420640-9800	Magnification 10x NA 0.3
Flip mirror	Thorlabs	CCM1-P01/M
Flip mirror mount	Thorlabs	FM90/M
L1-lens	Thorlabs	LA1986	f = 125 mm
L2-lens	Thorlabs	LA1461	f = 250 mm
Objective lens	Nikon	MUE10500	Magnification 50x NA 0.8
Pinhole	Thorlabs	ID8/M
Polarizer	Thorlabs	GTH10M	For LMOKE measurements, two polarizers are needed
sCMOS camera	Andor	ZYLA-4.2P-USB3