Спектральная и угловая магнитооптическая характеристика фотонных наноструктур

Резюме

Структура фотонической полосы позволяет понять, как ограниченные электромагнитные режимы распространяются в фотоническом кристалле. В фотонных кристаллах, которые включают магнитные элементы, такие замкнутые и резонансные оптические режимы сопровождаются усиленной и модифицированной магнито-оптической активностью. Мы описываем процедуру измерения для извлечения магнито-оптической структуры полосы с помощью космической микроскопии Фурье.

Аннотация

Фотонические кристаллы являются периодическими наноструктурами, которые могут поддерживать различные ограниченные электромагнитные режимы. Такие замкнутые режимы обычно сопровождаются локальным повышением интенсивности электрического поля, что укрепляет взаимодействие световой материи, позволяя приложениям, таким как поверхностное рассеяние Раман (SERS) и улучшение плазмонов поверхности. При наличии магнито-оптически активных материалов, локальное улучшение поля приводит к аномальной магнито-оптической активности. Как правило, ограниченные режимы данного фотонных кристаллов сильно зависят от длины волны и угла частоты инцидента электромагнитного излучения. Таким образом, для их полной идентификации, а также для установления их связи с магнитооптической активностью кристалла необходимы спектральные и угловато-разрешенные измерения. В этой статье мы описываем, как использовать микроскоп Fourier-plane (задний фокусный самолет) для характеристики магнито-оптически активных образцов. В качестве модели системы, здесь мы используем плазмонную решетку, построенную из магнито-оптически активного многослойного Au/Co/Au. В экспериментах мы применяем магнитное поле на решетке на месте и измеряем его ответ на взаимное пространство, получая магнитооптическую реакцию решетки на диапазон длин волн и углов инцидента. Эта информация позволяет нам создать полную карту плазмонной структуры полосы решетки и угла и длины волны зависимой магнито-оптической активности. Эти два изображения позволяют нам определить влияние, которое плазмонные резонансы оказывают на магнито-оптический ответ решетки. Относительно небольшая величина магнитооптических эффектов требует тщательного обработки приобретенных оптических сигналов. С этой целью выкладывается протокол обработки изображений для получения магнитооптического ответа от полученных необработанных данных.

Введение

Ограниченные электромагнитные режимы в фотонных кристаллах могут возникнуть из различных истоков, таких как плазмонные резонансы вокруг металлических/диэлектрических интерфейсов или резонансы Mie в высокорепрелодействующих индексных диэлектрических наноструктурах^1,2,3,и могут быть разработаны, чтобы появиться на специально определенных частотах^4,5. Их присутствие приводит к многим увлекательным явлениям, таким как фотонические пробелы полосы^6,7,8,сильная локализация фотона^9,медленный свет¹⁰ и конусы Дирака¹¹. Четырехмерная микроскопия и спектроскопия самолета являются основными инструментами для характеристики фотонных наноструктур, поскольку они позволяют захватывать многие существенные свойства ограниченных режимов, происходящих в них. В космической микроскопии Фурье, в отличие от обычной реальной плоскости изображения, информация представлена как функция угловых координат^12,13. Это также известный как задняя фокусная плоскость (BFP) изображения, как угловое разложение света, иссисходяго из образца регистрируется из задней фокусной плоскости микроскопа цели. Угловой спектр, т.е. схема излучения в дальней области образца, связан с импульсом света, исполнимого из него(к). В частности, он представляет свой в плоскости импульс (k_x,k_y) распределение¹⁴.

В магнито-оптически активных образцах, наличие ограниченных фотонных возбуждений, как было показано, приводит к значительному улучшению магнито-оптического ответа^{15,16,17,18,19}. Магнитно-оптические эффекты зависят от взаимной геометрии магнитного поля и инцидента электромагнитного излучения. Нарисунка на рисунке 1магнитооптические геометрии линейно поляризованного света и их номенклатуры. Здесь мы демонстрируем установку, которая может быть использована для изучения двух магнито-оптических эффектов, которые наблюдаются в отражении: поперечные и продольные эффекты магнито-оптического Керра, сокращенно, соответственно, как TMOKE и LMOKE. TMOKE – это эффект интенсивности, где отражательные эффекты противоположных состояний намагниченности различны, в то время как LMOKE проявляется как вращение оси поляризации отраженного света. Эффекты отличаются ориентацией намагниченности по отношению к заболеваемости светом, где для LMOKE, намагничивание ориентировано параллельно в плоскости компонента вектора волны света пока для TMOKE оно поперечно к ему. Для нормального света инцидента оба в плоскости компоненты импульса света являются нулевыми (k_x q k_y 0) и, следовательно, оба эффекта равны нулю. Конфигурации, где оба эффекта присутствуют можно легко зачат. Однако, чтобы упростить анализ данных, в этой демонстрации мы ограничиваемся ситуациями, когда присутствует только один из эффектов, а именно TMOKE.

Несколько оптических конфигураций могут быть использованы для измерения углового распределения света, излучаемого из магнитофотонных кристаллов. Например, в Kalish et al.²⁰ и Боровкове и др.²¹такая установка была успешно использована в геометрии трансмиссии для того, чтобы раскрыть плазмонное влияние на магнитооптические явления. В качестве иллюстрации в Kurvits et al.²²некоторые возможные конфигурации представлены для микроскопа, использующему объектив объективной линзы с исправленной бесконечностью. В нашей конфигурации, изображенной на рисунке 2A,мы используем экран из-под исправления бесконечности, где свет, исходящий от данной точки в образце, направлен объективом в коллинеарные лучи. На рисунке 2A,лучи, возникающие сверху (разбитые линии) и нижние (твердые линии) образца схематично изображены. Затем, собирая объектив использован для того чтобы переориентировать эти лучи для того чтобы сформировать изображение на плоскости изображения (IP). Второй объектив, также известный как объектив Бертрана, помещается после плоскости изображения, чтобы отделить входящий свет в фокусной плоскости на угловые компоненты, изображенные на рисунке 2А в красном, синем и черном цвете. Из этой задней фокусной плоскости угловое распределение света, излучаемого образцом, может быть измерено с помощью камеры. Фактически, объектив Bertrand выполняет преобразование Фурье на световом луче, прибосьявающее к нему. Распределение пространственной интенсивности в BFP соответствует угловому распределению излучения инцидента. Полную карту отражения пространства образца можно установить путем освещения образца с той же целью, которая используется для сбора ответа образца. Входящие и исходящие лучи разделены с помощью сплиттера. Полная установка изображена на рисунке 3А. Для получения спектра необходим настраиваемый источник света или монохроматор. Измерение может быть повторено на различных длинах волн, имея в виду, что из-за спектра стандартных источников света, результаты должны быть нормализованы к отражательной части контрольного образца. Для этого можно использовать зеркало или часть образца, который был намеренно оставлен без шаблона, чтобы обеспечить высокую отражательную способность. Чтобы помочь в позиционировании, мы покажем, как интегрировать установку с дополнительной оптической системой, которая позволяет реальной космической визуализации образца, показанного на рисунке 2B.

Теперь мы приступим к созданию метода измерения углового решена магнито-оптического спектра фотонического кристалла, используя в качестве репрезентативного образца, DVD решетки покрыты Au / Co / Au пленки, где наличие ферромагнитного кобальта приводит к значительной магнито-оптической активности²³. Периодическое гофрирование dvd решетки позволяет поверхности plasmon поляритон (SPP) резонансы на различных длина волны угол комбинации, которые даны

где n является рефракционным индексом окружающей среды, k₀ волновой вектор света в свободном пространстве,₀ угол частоты, d периодичность решетки и м является множеством, обозначающим порядок SPP. Вектор волны SPP 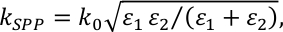дается где No₁ и No₂ являются разрешения металлическим слоем и окружающей диэлектрической средой. Из-за толщины многослойной пленки из золота/кобальта можно предположить, что ГЧП возбуждаются только поверх многослойной пленки.

протокол

1. Установка установки

1. Оптика
   ПРИМЕЧАНИЕ: Создайте установку, как показано на рисунке 3А на оптическом столе с достаточной изоляцией вибрации. Чтобы избежать сферических и других аберраций, центр все оптические компоненты (линзы, пинхолы и т.д.) по отношению к лучу. Оптическое расположение показано на рисунке 2 с указанными расстояниями между компонентами.
   1. Направляй свет от источника белого света к монохроматору, чтобы получить монохромный луч света. Подробную информацию о настройке, используемой в этой работе, можно узнать в таблице материалов. Установите монохроматор на длину волны, которая имеет хорошую интенсивность и видимость, например, 550 нм. Длина волны от видимой части спектра облегчает располагание оптических элементов.
   2. Используя соединительный объектив, соедините свет к волокну и сопутствоваем его с целью на прекращении волокна. В зависимости от используемого источника света этот шаг может быть опущен.
   3. Поместите поляризатор 250 мм от коллимирующего объектива, чтобы линейно поляризовать луч и поместите сплиттер пучка 100 мм от поляризатора, чтобы направить свет к объективу микроскопа объективной.
      ПРИМЕЧАНИЕ: Из-за коллимированного луча указанные позиции вышеупомянутых компонентов не влияют на оптику установки измерения и даются только для наведения.
   4. Поместите образец на держатель образца, оснащенный этапом перевода x-y-z и этапом вращения, который обеспечивает 360-градусное вращение образца вокруг оси z, т.е. ось света, посягающего на образец.
   5. Установите объектив объективной линзы на этапе перевода, что позволяет движение в трех направлениях. Наиболее важным из них является z-оси, которая необходима для фокусировки на образец.
      ПРИМЕЧАНИЕ: Необходимое оборудование для перевода образцов зависит от используемых образцов. Большие однородные образцы могут быть расположены вручную, в то время как образцы с небольшой полезной площадью потребуют более тщательного позиционирования, особенно при использовании пинхола для ограничения изображенной области (шаг 1.1.7.). Оптика луча, вытекающая из образца, схематично изображена на рисунке 2. Исправленная объективной линзой бесконечности направляет волновые фронты, возникающие из каждой точки образца, в коллинеарные лучи.
   6. Поместите коллекторский объектив с f й 200 мм (трубка объектив), 330 мм от цели, чтобы перефокусировать лучи, чтобы сформировать изображение на плоскости изображения. Благодаря коллинеарного распространения света, исссцирующегося из образца, линза коллектора может быть размещена на любом расстоянии от объектива цели.
      ПРИМЕЧАНИЕ: Как и прежде, свет, возникающий из объективного объектива, коллимируется. Тем не менее, трубка объектив должен быть помещен после сплиттера пучка.
   7. Поместите пинхол в плоскость изображения на 200 мм от объектива коллектора, чтобы ограничить изображенную область узорчатой областью. Поместите пинхол в центре луча. При использовании пинхола используйте реальное космическое изображение образца, чтобы позиционировать его. Для образцов, где узорчатая площадь больше, чем область, освещенная лучом света, это не обязательно.
   8. Поместите второй объектив с f 75 мм (объектив Бертран), 120 мм после плоскости изображения, чтобы создать Фурье преобразование угловых компонентов изображения. Преобразование создается в фокусе второго объектива и изображением с помощью научной камеры sCMOS, которая находится 75 мм от объектива Bertrand.
   9. Для измерений LMOKE вставьте дополнительный поляризатор с углом по отношению к первому поляризатору между сплиттером луча и объективом коллектора.
2. Магнит
   1. Подключите магнит к источнику питания и установите его так, чтобы магнитное поле можно было нанести на образец. Выберите, применяется ли магнитное поле в продольном, поперечном или полярном направлении(рисунок 1).
3. Подготовка образцов
   1. Механически демонтировать коммерческий DVD-диск; впоследствии экспонируемая поверхность решетки может быть легко идентифицирована из-за ее диффрапактивной приличия. Используйте клеевую ленту, чтобы очистить предыдущие покрытия. Очистите поверхность, замочите ее в этаноле в течение 10 минут. Решетка теперь готова к получению магнито-плазмонного покрытия.
      ПРИМЕЧАНИЕ: Различные коммерческие оптические диски, как Blu-Ray и компакт-диски, возможно, потребуется другой протокол подготовки.
   2. Депозит металлической пленки на открытой решетке путем испарения электронного луча. Для обеспечения низкой шероховатости используйте скорость испарения меньше 5 к/с.
   3. Начиная с 4 нм Cr клеевого слоя, депозит чередующихся золотистого и кобальтового слоев, заканчивая с золотым укупорки слоя для обеспечения защиты от окисления.
      ПРИМЕЧАНИЕ: Мы использовали следующее количество слоев и толщины: Cr (4 нм)/Au (16 нм)/Ко (14 нм)/Au (16 нм)» 4/Co (14 нм)/Au (7 нм).
   4. Выполните оптическую или электронную микроскопию(рисунок 4А)для проверки условий поверхности образца, в случае однородности и низких дефектов приступить к измерению.

2. Процедура измерения

1. Позиционирование образцов
   ПРИМЕЧАНИЕ: В качестве иллюстративного образца, мы будем измерять DVD решетки покрыты магнитоплазмонных Au / Co / Au фильма. Из-за периодического гофрирования решетки, САУ могут возбуждаться под определенным углом заболеваемости в зависимости от длины волны.
   1. Установите образец на держатель образца, используя небольшую каплю серебряной краски. Пусть серебряная краска высохнет в течение 10 мин.
   2. Вставьте флип-зеркало после плоскости изображения, чтобы обеспечить реальное космическое изображение образца. Вставьте объектив L1 с f й 125 мм, так что изображение плоскости находится в фокусе и место L2 с f й 250 мм на расстоянии 135 мм от L1.
   3. Наконец, поместите заряд-связанные устройства (CCD) камеры 210 мм от L2 для захвата увеличенное изображение плоскости изображения. Перемещение линзы L1 и L2 до пинхол помещены в плоскости изображения в хорошем фокусе на ccD камеры.
   4. Переместите объектив объективного объектива к образцу до тех пор, пока образец не будет в хорошем фокусе в камере CCD.
2. Измерение оптической отражательной способностью
   1. Используя реальное космическое изображение образца, расположите световое пятно над отражающей (неузорчатой) частью образца. Переверните флип-зеркало, чтобы увидеть BFP микроскопа.
      ПРИМЕЧАНИЕ: Здесь, для DVD-решетки мы используем непрерывную металлическую пленку на краю диска DVD.
   2. Выберите область задней фокусной плоскости, которая соответствует желаемому состоянию поляризации. Взаимосвязь между поляризовыванием и положением в задней фокусной плоскости показана на рисунке 3B. Выберите область интереса (AOI) в виде прямоугольного сечения объективного задней фокусной плоскости (синий прямоугольник на рисунке 3C)вдоль оси, которая соответствует ТМ-поляризации.
      ПРИМЕЧАНИЕ: В программном обеспечении приборов, используемом в этой рукописи, это достигается путем выбора AOI с помощью селекторов курсора. Программное обеспечение затем усредняет интенсивность вдоль короткого измерения прямоугольника и рассматривает полученный спектр как 1D массив данных, где каждая точка данных соответствует другому углу выбросов образца. В плазмонных решетках только ТМ-поляризованный свет, т.е. ЭМ-излучение с электрическим полем, перпендикулярно решетке, может возбуждать плазмонные резонансы. Таким образом, в зависимости от ориентации решетки, необходимо выбрать правильное состояние поляризации, выбрав вертикальный или горизонтальный срез BFP.
   3. Измерьте спектр источника света, нажав спектр нормализации измерения,который будет использоваться позже для нормализации измеренных данных отражения. Поскольку каждая длина волны дает 1D набор точек данных, весь спектр источника света сохраняется как 2D тензор, где каждая точка данных представляет собой сочетание длины волны и угла.
   4. Используя снова реальное изображение пространства образца, положение источника света над фотон кристаллом интереса. При переключении обратно в BFP, убедитесь, что режимы плазмон видны как темные линии, пересекающие заднюю фокусную плоскость. Линии движутся по мере изменения длины волны света инцидента.
   5. Используя те же параметры AOI и измерения (т.е. время экспозиции, количество средних), измеряйте спектр отражения фотонных кристаллов, нажав спектр отражения измерения.
   6. Чтобы учесть спектральные изменения интенсивности источника света, нормализуем полученный спектр по спектру источника света. Это даст 2D массив чисел от 0 до 1, где 1 соответствует полностью отражающей и 0 полностью абсоративных условиях.
3. Магнитооптическое измерение
   1. Начните магнито-оптическое измерение путем измерения петли гистерезсс с помощью угла и длины волны, которые, как известно, соответствуют хорошей магнито-оптической реакции, как правило, эти условия могут быть найдены близко к sPP возбуждения. Для этого выберите небольшой AOI вблизи возбуждений SPP и измерьте один цикл.
      ПРИМЕЧАНИЕ: Анализ данных, необходимый для количественной оценки магнито-оптической активности, зависит от типа магнетизма, который проявляет образец. Здесь мы берем на себя ферромагнитную реакцию и относимся к результатам соответствующим образом. Диа- или парамагнитной реакции по существу линейной прикладного магнитного поля и может быть количественно, как изменение оптических свойств на прикладной единицы магнитного поля. Ферромагнитные материалы обладают нелинейной беспределом, которая требует дополнительного рассмотрения при определении магнито-оптического ответа (см. рисунок 3D). TMOKE определяется как изменение отраженной интенсивности как функция прикладного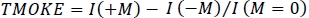 магнитного поля, т.е. когда I(M) является интенсивность, отраженная образцом при состоянии намагниченности M.
   2. Используя петлю гистереза, измеренную в 2.3.1., выберите диапазон магнитных полей для цикла. Для ферромагнитных образцов цикл поля от полностью насыщенного состояния до противоположнонасыщенного состояния, расширяя диапазон комфортно над полем насыщения. Позже используйте точки, измеренные в насыщенном состоянии, для анализа и удаления любых диа- или парамагнитных вкладов, которые могут быть проверены их линейным вкладом.
   3. Наконец, измерьте интенсивность, отраженную в образце в каждой определенной точке магнитного поля, повторяя при желании несколько петель. Каждая длина волны и точка намагничивания дают единый 1D массив численных данных (т.е. измеренную интенсивность света), где каждая точка массива соответствует определенному углу.

3. Анализ данных

1. Используя цикл гистерезы образца, измеренного на шаге 2.3.1, присвоите каждый кадр, измеренный на шаге 2.3.3. в любом из насыщенных состояний или в промежуточном состоянии(рисунок 3C).
2. Откажитесь от промежуточных кадров и вычислите магнито-оптическую активность из измеренной интенсивности по 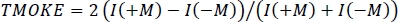, где операции выполняются отдельно для каждой угловой и длины волны данных точки.
   ПРИМЕЧАНИЕ: Как TMOKE выражается как относительная интенсивность изменения, результаты не должны быть нормализованы для спектра лампы.
3. Если в образце представлена большая парамагнитная (или реже диамагнетная) активность, которую необходимо вычесть для надежного сравнения насыщенных магнитных состояний, вычесть линейный вклад, возникающий в результате пара- или диамагнитной активности, линия (опять же, pixelwise отдельно для каждого угла и длины волны точки) на точки, измеренные при насыщении и удалить линейный вклад.

Результаты

На рисунке 4А показан сканирующий электронный микроскоп (SEM) микрограф коммерческой DVD решетки, покрытой многослойной Au/Co/Au, которая использовалась демонстрационным образцом в наших экспериментах. Его оптические и магнито-оптические спектры показаны на

Обсуждение

Мы ввели установку измерения и протокол для получения угловато-разрешенных магнито-оптических спектров оптических кристаллов. В частности, был изложен случай ферромагнитных материалов, требующих дополнительного анализа данных для учета нелинейной проницаемости материала. Угловая р...

Материалы

Name	Company	Catalog Number	Comments
Beam splitter	Thorlabs	BSW27
Bertrand lens	Thorlabs	LA1608	f = 75 mm
CCD Camera	Thorlabs	1500M-GE-TE	Camera for real space imaging
Collecting lens	Thorlabs	ITL200	f = 200 mm
Collimating lens	Zeiss	420640-9800	Magnification 10x NA 0.3
Flip mirror	Thorlabs	CCM1-P01/M
Flip mirror mount	Thorlabs	FM90/M
L1-lens	Thorlabs	LA1986	f = 125 mm
L2-lens	Thorlabs	LA1461	f = 250 mm
Objective lens	Nikon	MUE10500	Magnification 50x NA 0.8
Pinhole	Thorlabs	ID8/M
Polarizer	Thorlabs	GTH10M	For LMOKE measurements, two polarizers are needed
sCMOS camera	Andor	ZYLA-4.2P-USB3