用于计算分子聚合和固体光学吸收光谱和光电特性的外化学汉密尔顿

摘要

在这里，我们提出了一个协议，用于从第一原理量子化学计算中计算分子材料的光吸收光谱和光电子特性的紧密结合外物质。

摘要

用于光电子应用的无序分子聚合和固体的合理设计依赖于我们使用理论和计算方法预测此类材料性能的能力。然而，大型分子系统，其中紊乱太严重，不能考虑在扰动极限，不能用第一原则量子化学或波段理论描述。多尺度建模是了解和优化此类系统的光电子特性的一种有前途的方法。它使用第一原理量子化学方法计算单个分子的特性，然后根据这些计算构建分子聚合体或散装材料的汉密尔顿人模型。在本文中，我们提出了构建紧密结合的汉密尔顿语的协议，该协议代表在Frenckel兴奋点基础上的分子材料的兴奋状态:电子孔对，这些对在构成材料的单个分子上局部化。这里提出的汉密尔顿参数化解释了分子之间的异质耦合，以及通过周围分子的电荷分布对分子上的电子密度的静电极化。这种模型汉密尔顿人可以用来计算光学吸收光谱和分子聚合和固体的其他光电子特性。

引言

在过去的二十年里，由聚合有机分子制成的固体和薄膜在光电子器件中找到了多种应用。基于此类材料的设备具有许多吸引人的性能，包括重量轻、灵活性强、功耗低，以及使用喷墨打印进行廉价生产的潜力。基于有机发光二极管（OLED）的显示器正在取代液晶显示器，作为手机、笔记本电脑、电视机和其他电子设备^{11、2、3、42,3,4}的先进设备。OLED在照明应用方面的重要性预计在未来⁴年会增加。有机光伏器件的性能稳步提高，最近单结有机太阳能电池^的功率转换效率超过16%。有机材料还有可能破坏其他技术，如光纤通信，其使用使光电调制器的带宽高达15 THz及以上^66，7。7

优化光电子应用的固态分子材料的一个主要挑战是，其特性通常在很大程度上取决于材料的纳米级结构。生产过程允许使用受控生长技术（如化学气相沉积、^将光学活性分子分泌到另一材料（即聚合物基质^{9,9、10）、}热退火^11、12,12等，在一定程度上定义材料的纳米结构。然而，纳米级紊乱是大多数分子材料固有的，通常不能完全消除。因此，了解无序如何影响材料的特性，并找到方法，以达到最佳性能，对于有机光电子材料的合理设计至关重要。

分子材料紊乱的程度通常太大，不能将其视为周期性晶体结构的扰动，其电子结构可以通过波段理论来描述。另一方面，在模拟中必须包括以重现散装材料或薄膜特性的分子数量太大，无法使用密度函数理论（DFT）13、14和时间相关密度函数理论（TD-DFT）15、16等第一原理量子化学方法。^{13,14 15,16}在光电子中的应用有机分子通常具有相对较大的+偶联系统;许多人也有捐助者和接受者团体。捕捉这些分子中正确的电荷转移行为对于计算其光电子特性至关重要，但只能使用TD-DFT^{17、18、19、20,19,}中的远程校正混合功能来完成。^17,20使用这种功能的计算与系统的大小线性缩放，目前，它们只可用于对单个有机分子或小分子聚合的光电特性进行建模，这些特性可以使用不超过±10⁴原子基础函数进行描述。一种可以描述由大量色光荷组成的无序材料的模拟方法对于对这些系统的建模非常有用。

分子材料中分子间相互作用的大小通常与构成材料的各个分子之间的能量参数（如能量或激发能量）的变化顺序相当或小于。在这种情况下，多尺度建模是了解和优化大型无序分子系统的光电子特性的最有希望的方法^{21、22、23。,22,23}这种方法使用第一原则量子化学方法（通常是DFT和TD-DFT）来精确计算构成材料的各个分子的特性。然后，使用为单个分子计算的参数构造足够大以表示大分子材料的材料样本的 Hamiltonian（也许，通过使用周期性边界条件）。然后，这个汉密尔顿人可以用来计算大分子聚合、薄膜或大分子材料的光电参数。

Exciton模型是多尺度模型的一个子类，其中分子材料的兴奋状态以兴奋度为基础表示:由库仑吸引力^24、25,25绑定的电子孔对。为了模拟许多兴奋状态过程，只包括Frenkel兴奋^26，其中电子和孔在同一分子上局部化就足够了。电荷转移冲锋，其中电子和孔是局部在不同的分子上，可能需要包括在某些情况下（例如，建模电荷分离在供体受体系统^）27，,28。虽然exciton模型是多尺度模型，只能对单个分子进行第一原理计算，但它们仍然包含分子间相互作用。他们可以解释的两种主要相互作用类型是:（a） 分子之间的兴奋耦合，这些分子具有兴奋剂在分子之间去局部或转移的能力，以及 （b） 通过周围分子上的电荷分布对分子上电子密度的静电极化。我们之前已经表明，这两个因素对于模拟分子聚合的光和光电特性都很重要，例如光学吸收光谱²⁹和第一个超极化^30。

在本文中，我们提出了一种用于计算大分子聚集体和散装分子材料的光学光谱和其他光电子特性的异化外物质模型的协议。外行汉密尔顿被认为是一个紧密绑定汉密尔顿^{24，25，24,}

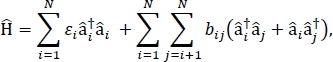
其中_#i是物质中^ith分子的i激发能量，b_ij是i^th和jth^th分子之间的兴奋耦合_，[i]^†和]_我分别是物质中ith^th分子的激发状态的创造和毁灭运算符。使用TD-DFT计算在构成材料的单个分子上进行，发现外向汉密尔顿参数。在这些TD-DFT计算中，材料中所有其他分子的电荷分布由静电嵌入原子点电荷来表示，以考虑分子电子密度的静电极化。单个分子的激发能量_#i，直接从TD-DFT计算输出中取走。分子之间的外向耦合b b_ij使用过渡密度立方体方法³¹计算，具有从高斯^32TDFT计算输出和使用多功能波函数分析仪³³进行后处理的相互作用分子的接地到兴奋状态过渡密度。为了模拟散装分子固体的特性，周期性边界条件可应用于汉密尔顿。

当前协议要求用户有权访问高斯³²和Multiwfn³³程序。该协议已经使用高斯16、版本 B1 和Multiwfn版本 3.3.8 进行了测试，但也适用于这些程序的其他最新版本。此外，该协议使用自定义C++实用程序和一些自定义 python 2.7 和 Bash 脚本，源代码在 https://github.com/kocherzhenko/ExcitonicHamiltonian 时在 GNU 通用公共许可证（版本 3）下提供。计算旨在从 Unix/Linux 系列运行操作系统的计算机上执行。

研究方案

1. 将多分子系统分裂为单个分子

1. 生成需要以三脚管理系统 MOL2 分子文件格式构建的系统结构。该结构可以是分子动力学或蒙特卡罗系统模拟的快照。
2. 如果系统中的所有分子由相同数量的原子组成，请使用 python 2.7 脚本getMonomers.py生成包含组成系统的各个分子中原子的笛卡尔坐标的文件。构成系统的分子不必相同（例如，它们可以是等构体）。此脚本采用两个输入参数。
   1. 指定包含步骤 1.1（字符串）中系统几何形状的 Tripos MOL2 文件的名称。
   2. 指定构成系统的每个单个分子中的原子数（整数）。要完成此步骤，请使用以下命令:
      ./getMonomers.py YLD124-300K_0-210000.mol2 125
      取取 Github 上的示例文件 YLD124-300K_0-210000.mol2 中包含的结构;以XYZ格式将单个分子的笛卡尔坐标写入n.commonomer_文件，其中N是一个四位数字，用于识别系统中的分子。
3. 如果系统由具有不同原子数的分子组成，则使用替代脚本或手动生成单个分子的结构。后续步骤中描述的过程无需任何修改即可使用。

2. 为单个分子中的原子产生接地状态点电荷

1. 设置纯文本文件chargeOptions.txt，其中的选项用于在电中性分子的接地状态下计算原子点电荷的高斯DFT。为了获得具有电荷转移字符的转换的合理准确的电荷分布，建议按如下方式指定参数。
   1. 使用长距离校正密度功能（如 +B97X）³⁴。
   2. 使用足够大的基础集，包括非氢原子（如6-31G+）35、36上的至少d极化^35,36函数。
   3. 使用超细集成网格。
   4. 使用非常紧密的自一致的场收敛标准（能量收敛到^10~10 Hartree）。
   5. 使用适合在分子附近重现静电电位的原子点电荷，如 CHelpG 方法³⁷中所做的那样，因为计算出的原子电荷将用于表示静电环境。
      注:在典型的分子聚合和固体分子之间的距离是相对较大的，所以通常可以接受使用其他原子点电荷定义，如Mulliken电荷^38。
   6. 在输入文件中包括NoSymm关键字，以确保高斯输出文件中的原子坐标以输入方向而不是标准方向写入。
   7. 在高斯输入文件的注释行中指定计算的名称。
   8. 在单独的行中指定分子的电荷和多重性（分别为 0 和 1）。文件 chargeOptions.txt 中指定的示例计算选项可以是:
      #p wB97X/6-31G= 积分（网格=超细网格）NoSymm SCF（Conver=10） Pop_CHelpG
      单体费用
      0 1
2. 使用文件 chargeOptions.txt 中的参数为组成系统的所有单个分子设置高斯输入文件。此步骤可以使用以下 Bash 脚本高效地完成:
   monomer__.xyz 中 f
   做
   猫收费选项.txt > $\f%xyz_com
   尾部 -n +3 $f >> $_f%xyz_com
   回声">> $_f%xyz_com
   做
   注: 该脚本将生成与步骤 1.2 中生成的 XYZ 文件同名的高斯输入文件，但使用扩展名.com。这些文件将包含在 chargeOptions.txt 中指定的计算选项和从相应的.xyz文件中指定的原子坐标，由空白行终止。
3. 运行高斯计算，指定输出文件名与输入.com文件名相同，但使用扩展名.log。
4. 使用扩展名.log从高斯输出文件中提取 CHelpG 原子点电荷，使用 python 2.7 脚本getCHelpG.py。该脚本采用 2 个输入参数:带有扩展名 .log的高斯输出文件的名称和单个分子中的原子数。
   注: 脚本getCHelpG.py编写与高斯输出文件同名但扩展名.chg的文件。这个文件有4个列:前三列与分子中原子的笛卡尔坐标，最后一列带有CHelpG原子点电荷。以下 Bash 脚本可以有效地从所有文件中提取费用:
   f 在 monomer__.log 中;做 ./getCHelpG.py $f N;做
   （N是分子中的原子数。
5. 如果在步骤 2.1 中使用了 CHelpG 以外的原子点电荷定义，请使用备用脚本或手动从高斯输出文件中提取电荷。

3. 在静电环境中计算材料中单个分子的激发能量和过渡密度

1. 设置纯文本文件，单体Options.txt，选项为高斯TD-DFT计算兴奋状态能量和接地到兴奋状态过渡密度矩阵为单个单体。建议的参数与步骤 2.1 中用于计算原子点电荷的参数相同。
   1. 使用范围分离的密度功能，如 #B97X³⁴。
   2. 使用足够大的基础集，包括非氢原子（如6-31G+）35、36上的至少d极化^35,36函数。
   3. 使用超细集成网格。
   4. 使用非常紧密的自一致的场收敛标准（能量收敛到^10~10 Hartree）。
   5. 包括NoSymm关键字，以确保高斯输出文件中的原子坐标以输入方向而不是标准方向写入;
   6. 为了获得合理准确的过渡密度，应将 eigenvector 组件的打印阈值设置（即，对 eigenvector 贡献非常小的基础函数的系数（理想情况下，至少为^10+5）应打印到输出文件中）。
      注: 要设置此条件，需要使用高斯内部选项:将叠加 9、选项 40 设置为用于打印 eigenvector 组件阈值的指数的绝对值（例如 IOp（9/40） = 5 将截止阈值设置为 10⁺⁵）。
   7. 在高斯输入文件的注释行中指定计算的名称。
   8. 在单独的行中指定分子的电荷和多重性（分别为 0 和 1）。在文件单体选项.txt 中指定的示例计算选项可以是:
      #p tda（NSs_10） wB97X/6-31G= 积分（网格=超细网格）NoSymm SCF（Conver=10） iop（9/40=5）
      带费用的单体
      0 1
2. 设置高斯输入文件，用于计算材料中所有单个分子的激发能量和过渡密度，在以材料中所有其他分子的点电荷表示的静电环境中，文件名称monomer_N_wCh.com。
   1. 在高斯输入文件中包括Gaussian保存带有文件名monomer_N_wCh.chk的文件的请求。
      注:对于该协议中描述的命名约定，此步骤可以使用 python 2.7 脚本getMonomerWCh.py在文件单体Options.txt中指定的计算选项中读取，在 n .xyz monomer_N文件中存储系统中单个分子的原子坐标，以及存储在monomer_ n .chg（N）N文件中的所有单个分子的原子点电荷。N
3. 运行高斯计算，指定输出文件名与输入.com文件名相同，但使用扩展名.log。计算还将保存具有相同文件名的检查点文件，但使用扩展名.chk。

4. 从高斯输出文件中提取组成系统的各个分子的明亮状态的激发能量

1. 使用扩展名.log将单个单体明亮的激发状态的激发Gaussian能量复制到称为all_energies.txt的纯文本文件。
   注: 如果只有一个明亮的激发状态，并且所有高斯输出文件都在同一目录中，那么此步骤可以通过创建一个空纯文本文件all_energies.txt，然后附加输出文件中的行，其中包含每个单体使用以下 Bash 脚本的明亮状态的激发能量:
   用于单体_WCh.log 中的 f;做grep"兴奋状态M"$f>> all_energies.txt;做
   （M是激发明亮状态的编号;单词状态和数字M之间的空格数应与高斯输出文件中的空格数相同。
2. 在文件all_energies.txt中，只保留包含激发能量的数值的列（在 eV 中）;删除所有其他列。

5. 计算构成分子系统的所有分子对的兴奋耦合

1. 使用作为高斯语一部分的 formchk 实用程序，使用以下 Bash 脚本将检查点文件转换为人类可读格式:
   monomer__.chk 中的 f;做 $f;做
   注: 人可读格式化的检查点文件的名称与原始检查点文件相同，但具有扩展名.fchk。
2. 使用 python 2.7 脚本switchSign.py，该脚本将高斯输出文件的名称与扩展名.log以及计算中包含的激发状态N作为输入参数的数量。
   注:如果接地状态永久偶极子矩矢量与地面向首次激发状态转换的过渡偶极子位向之间的角度是迟钝的，则此脚本打印出.log文件的内容，将过渡偶极子矩矢量的方向从地面切换到所有兴奋状态。
3. 将脚本生成的输出switchSign.py保存到与.log文件同名但具有扩展名.log2的文件。
4. 对于接地状态永久偶极子矩矢量与地面向首次激发状态转换的过渡偶极子位向之间的角度为急性的分子，请将.log文件复制到具有相同名称和扩展名.log2的文件。
   注: 如果使用此协议中建议的命名约定，则可以使用以下 Bash 脚本为所有单个单体高效地完成步骤 5.2_5.4:
   在单体__wCh.log 中为 f
   做
   ./switchSign.py $f 10 > $f_2
   如果 [ s $f_2 ]
   然后
   回声"切换过渡偶极子时刻符号"$f
   还
   回声"复制"$f'到' $f_2
   cp $f_ $f_2
   菲
   做
5. 使用Multiwfn多功能波函数分析器基于高斯格式化的检查点文件编写过渡密度多维数据集文件，扩展名.fchk和使用扩展名.log2处理的高斯输出文件。
   注:高斯仅本机支持将空间密度分布保存到密度立方体文件中，以便与赫米蒂安运算符对应的可观测值。由于过渡密度运算符不是 Hermitian，因此需要后处理程序才能获得密度多维数据集文件。
   1. 启动Multiwfn程序。
   2. 将高斯格式化的检查点文件（在步骤 5.1 中生成的扩展名.fchk的文件）作为输入文件。
   3. 从主函数菜单中选择选项 18，电子激励分析。
   4. 从电子激励分析菜单中选择选项1，分析和可视化孔电子分布、过渡偶极点和过渡密度。
   5. 当提示输入高斯输出文件的路径或包含激发数据的纯文本文件时，提交带有过渡偶极子矢量调整符号的高斯输出文件（扩展名.log2保存在步骤 5.2 中的文件）。
   6. 指定应为其生成过渡密度多维数据集文件的过渡（如果只有一个亮状态，则它是从地面状态到该状态的过渡）。
   7. 在下一个菜单中选择选项1，可视化和分析孔、电子和过渡密度等。
   8. 选择将为其生成过渡密度多维数据集文件的网格中的点数:更多的点导致更精确的兴奋耦合，但大大延长计算时间，在大多数情况下，选项 1，低质量网格，覆盖整个系统，总共约 125000 点就足够了。
   9. 选择选项 13，在下面的菜单中选择转换密度到当前文件夹的输出多维数据集文件。将写入过渡密度多维数据集文件transdens.cub，重命名此文件的名称与.log2和.fchk文件的名称相同，扩展名.cub.
      注: Multiwfn旨在以交互方式运行，从键盘输入计算选项以响应提示。但是，设置具有处理选项的文件，然后让Multiwfn从该文件读取它们更为方便。
6. 要有效地生成包含当前目录中所有.fchk文件的Multiwfn处理选项的设置文件，请使用 bash 脚本makeOpt.sh。脚本makeOpt.sh编写的文件的名称与扩展名.opt .opt .
7. 使用以下 Bash 脚本在单个批处理中生成过渡密度多维数据集文件:
   用于单体__wCh.fchk 中的 f
   做
   多wfn$f < $_f%fchk_选择
   mv transdens.cub $_f%fchk_cub
   做
   注:图1显示了分子2-~4-（E，3E）-3-3-[E]-2-[4-比2_2-ter-丁基-（二甲基）硅=羟基_氨基_苯基_乙酰]-5，5-二甲基环氧乙基-2的转换密度 -en-1-伊利德内_prop-1-enyl_-3-氰-5-苯-5-（三氟甲基）富兰-2-伊利德内_丙二烯（俗称YLD 124 [Jen2005]）39在周围分子的点电荷存在。³⁹
8. 将.cub文件转换为文件，这些文件显式指定步骤 5.5.8（前 3 列）中使用的网格上所有多维数据集的中心坐标，以及使用 python 2.7 脚本cubeFormat.py多维数据集内过渡密度的值。该脚本以.cub文件的名称作为输入。要转换目录中的所有.cub文件，请使用 Bash 脚本:
   monomer_0_.cub;$f回音;./cubeFormat.py $f;做
   注: 脚本cubeFormat.py编写一个格式化的密度多维数据集文件，其名称与它采用的输入文件相同，但使用扩展名.fcub。
9. 使用步骤 5.8 中生成的.fcub文件，使用过渡密度立方体方法³¹计算系统中所有分子对之间的兴奋耦合。此步骤可以使用 cubePairGen 程序完成，该程序为不同的分子获取两个 .fcub 文件作为输入。要运行它，请使用 以下命令:
   ./立方配对根monomer_N_wCh.fcub monomer_M_wCh.fcub
   注:程序返回一个名为coup_N=M的文件，该文件包含一条包含三个数字的行:分子编号N和M，然后是 eV 中这两个分子之间的兴奋耦合。可以使用 GNU 编译器集合中的C++编译器编译文件 CubePairGen.cpp 中的程序源代码，并包含以下命令:
   g_ 立方体配对根.cpp _o 立方体配对根
10. 如果使用此协议中建议的文件命名约定，则可以将计算作为构成所研究系统的所有单个分子对的批处理运行。要运行这些计算，请使用以下 Bash 脚本:
    在 @.fcub 中 f
    做
    g 在 +.fcub
    做
    ff_$$\f_monomer_]
    gg_$_g_monomer_]
    fff=$$_ff%_wCh]
    ggg_${gg%_wCh]
    如果 [ $fff" -gt "$ggg" |
    然后
    （*） ./立方Pairgen"$f $g"coup_"$fff_'$$ggg]
    菲
    做
    做
    注:图2显示了用于计算这些分子之间的异常耦合的YLD 124的两个分子的过渡密度。对于分子对总数较大的大型系统，可以修改 Bash 脚本中星号标记的线，以便将计算提交到超级计算群集的排队系统。
11. 完成步骤 5.8 中的计算后，创建空文件all_couplings.txt，并使用以下 Bash 脚本将所有异常耦合合并到单个文件中:
    coup_0*;做猫$f >> all_couplings.txt;做

6. 设置前科汉密尔顿

1. 将步骤 4.2 中生成的文件all_energies.txt中的兴奋状态能量和在步骤 5.9 中生成的文件all_couplings.txt中的 excitonic 耦合组合组合合并到一个文件中，其中包含使用 2.7 脚本SetupHam.py使用终端命令的完整 excitonic Hamilton 矩阵:
   ./Setup_Ham.py all_energies.txt all_couplings.txt N >汉密尔顿.txt
   注: 程序将编写一个包含三列的文件 Hamiltonian.txt:每个矩阵元素的行号、列号和值（eV），行由空白行分隔。
   1. 指定包含外音能量的文件的名称。
   2. 指定包含外向耦合的文件的名称。
   3. 指定汉密尔顿矩阵的尺寸N（系统中的分子数）。

结果

在本节中，我们介绍了计算六个YLD 124分子聚合的光吸收光谱的代表性结果，如图3a所示，其中聚合的结构是从粗粒度的蒙特卡罗模拟中获得的。YLD 124是一种典型的电荷转移色电，由一个电子捐赠组二甲酰胺组成，该保护组通过+-偶联桥连接到电子接受组2-（3-氰-4，5，5-三甲基-5H-furan-2-伊利德内）-马龙石^39。该分子具有较大的接地状态偶极子矩，对单?...

讨论

此处介绍的方法允许多个自定义。例如，可以修改 DFT 和 TD-DFT 计算的参数，包括密度函数、基集和原子点电荷的特定定义。

建议使用长距离校正功能，如 #B97X、#B97XD 或 #PBE，以便获得具有电荷传输字符的转换的合理过渡密度。研究功能的特定选择（或功能参数，如精确交换量或范围分离参数* 的值）对特定系统^{42、43、4443,44}

材料

Name	Company	Catalog Number	Comments
Gaussian 16, revision B1
Multiwfn version 3.3.8
GNU compiler collection version 9.2
python 2.7.0