模拟人脑空间导航的功能网络

摘要

本文提出了一种研究人脑空间导航功能网络的综合方法。这种方法结合了大规模神经影像元分析数据库、静息态功能磁共振成像以及网络建模和图论技术。

摘要

空间导航是一项复杂的功能，涉及多感官信息的整合和操作。使用不同的导航任务，在各种大脑区域（例如海马体、内嗅皮层和海马旁位置区域）的特定功能上取得了许多有希望的结果。最近，有人提出，涉及多个相互作用的大脑区域的非聚集网络过程可以更好地表征这种复杂功能的神经基础。本文提出了一种构建和分析人脑空间导航功能特异性网络的综合方法。简而言之，这种综合方法包括三个主要步骤:1）识别对空间导航很重要的大脑区域（节点定义）;2）估计这些区域中每一对之间的功能连通性，并构建连通性矩阵（网络构造）;3）研究所得网络的拓扑特性（例如，模块化和小世界性）（网络分析）。从网络的角度来看，所提出的方法可以帮助我们更好地理解我们的大脑如何在复杂和动态的环境中支持灵活的导航，并且揭示的网络拓扑特性还可以为指导临床实践中阿尔茨海默病的早期识别和诊断提供重要的生物标志物。

引言

功能特异性是人脑的基本组织原则，在塑造认知功能方面起着至关重要的作用¹.功能特异性组织的异常可以反映标志性的认知障碍和主要脑部疾病（如自闭症和阿尔茨海默病）的相关病理基础 ^2,3。虽然传统理论和研究倾向于关注单个大脑区域，例如用于面部识别的梭形面部区域 （FFA）⁴ 和用于场景处理的海马旁位置区域 （PPA）⁵，但越来越多的证据表明，复杂的认知功能，包括空间导航和语言，需要跨多个大脑区域的协调活动⁶.研究支持复杂认知功能的相互作用背后的机制是一个关键的科学问题，将有助于阐明大脑的功能结构和操作。本文以空间导航为例，提出了一种对人脑空间导航功能网络进行建模的综合方法。

空间导航是一种复杂的认知功能，它涉及多个认知组件的整合和操作，如视觉空间编码、记忆和决策⁷.通过功能性磁共振成像 （fMRI），许多研究在理解潜在的认知处理和神经机制方面取得了重大进展。例如，使用各种导航任务将特定功能与不同的大脑区域联系起来:场景处理与 PPA 特别相关，导航策略的转换与脾后皮层 （RSC^{） 相关8,9}。这些研究为空间导航的神经基础提供了重要的见解。然而，导航是一种内部动态和多模态功能，单个区域的功能不足以解释通常观察到的空间导航¹⁰中的巨大个体差异。

随着基于fMRI的连接组学的出现，研究人员开始探索一些关键的大脑区域如何相互作用以支持空间导航。例如，已发现内嗅和后扣带回皮层之间的功能连接是高危阿尔茨海默病¹¹ 导航差异的基础。在另一项研究中，我们首次提出了一种网络方法，将连接组方法和几乎所有功能相关的区域（节点）整合在一起进行空间导航，结果表明该网络的拓扑特性与导航行为具有特定的关联¹²。这项研究为多个大脑区域如何相互作用以支持灵活导航行为的理论提供了新的见解^10,13。

本工作展示了用于功能网络建模的集成方法的更新版本。简而言之，包括两项更新:1）虽然原始研究中定义的节点是基于更早和较小的数据库（55项研究，2,765次激活，2014年访问），但目前的定义是基于最新的数据库（77项研究，3,908次激活，2022年访问）;2）为了增加每个节点的功能同质性，除了原始的解剖学AAL（解剖学自动标记）图谱¹⁴外，我们还应用了一种新的脑包裹，它具有更精细的分辨率和更高的功能同质性（见下文）。我们预计这两项更新都将改进功能网络的建模。这个更新的协议提供了一个详细的过程，从网络的角度研究空间导航的神经基础，并有助于理解健康和疾病中导航行为的个体差异。类似的程序也可用于其他认知结构（例如，语言和记忆）的网络建模。

研究方案

注意:此处使用的所有软件都显示在 材料表中。本研究中用于演示目的的数据来自人类连接组项目 （HCP: http://www. humanconnectome.org）¹⁵。所有实验程序均已获得华盛顿大学机构审查委员会（IRB）的批准。HCP 数据集中的成像数据是使用带有 32 通道头线圈的改进型 3T 西门子 Skyra 扫描仪获取的。其他图像采集参数详见早先的论文¹⁶。为演示下载了最少的预处理数据，该演示已完成以下预处理步骤:梯度失真校正、运动校正、场图预处理、空间失真校正、蒙特利尔神经学研究所 （MNI） 空间空间归一化、强度归一化和偏置场去除。也可以使用来自研究人员项目的静息态fMRI数据。

1. 数据预处理

1. 检查数据质量并排除缺少重测数据和头部运动过度（平移 3 毫米和旋转 3°）的参与者。
   注:5名受试者被移除，38名年轻人（22-35岁）被纳入主要分析。
2. 在 MATLAB 中打开图理论网络分析 （GRETNA） 工具箱¹⁷ ，执行进一步的预处理步骤。单击" FC Matrix Construction"批次。选择功能数据集的路径以加载 NIFTI 文档并执行以下步骤，如 图 1 中的管道选项所示:
   1. 通过双击"删除第一个图像"中的"要删除的时间点编号"并输入 10，删除前 10 个图像。
   2. 空间平滑（半高全宽 [FWHM] = [4 4 4]，在空间平滑中双击 FWHM （mm） 并输入 [4， 4， 4]）。
   3. 回归协变量。选择"白质信号"、"脑脊液信号"和"头部运动"为"TRUE"。根据实际体素大小选择合适的蒙版，例如，此处的 2 mm 蒙版，头部运动选择 Friston-24 参数。
   4. 时间过滤器。根据 MRI 扫描的重复时间输入 TR 的值（例如，此处为 720 ms），并通过双击 频段 （Hz） 并输入 [0.01 0.1] 来消除高频和低频噪声。
      注意:有和没有全脑信号回归的结果如下所示。当使用未预处理的数据时，还建议使用完善的管道，例如 fMRI-prep¹⁸ 和静息态 fMRI 数据处理助手 （DPARSF）¹⁹ 。

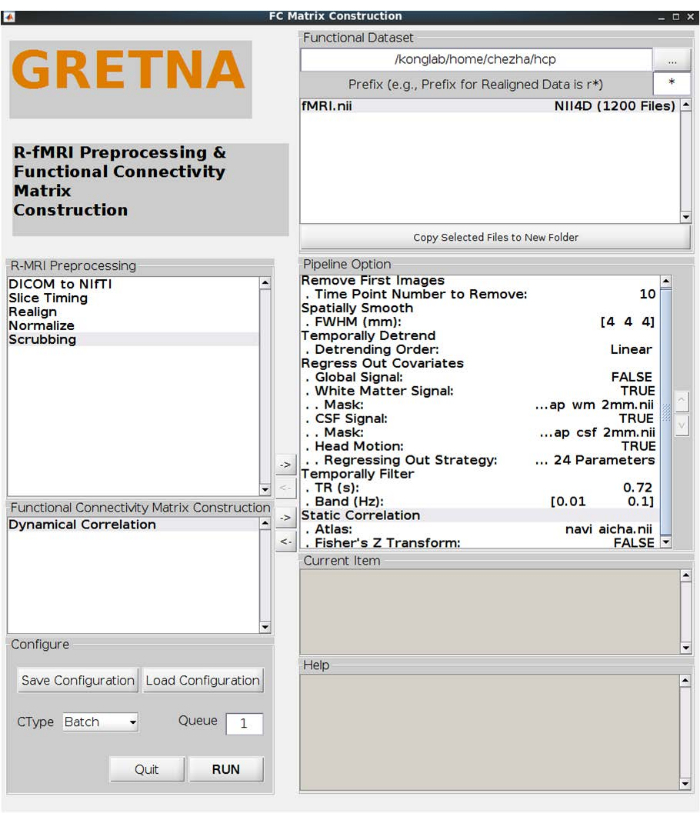
图 1:Rs-fMRI 预处理和功能网络连接估计。 预处理的设置（去除前 10 张图像、使用 4 mm 的 FWHM 进行空间平滑、线性时间去趋势、回归白质信号、脑脊液 （CSF） 信号和头部运动的 24 个参数，过滤 0.01-0.1 HZ 的波段）以及与 fisher' Z 的静态相关性变换。缩写:Rs-fMRI = 静息态功能磁共振成像;FWHM = 半高全宽;CSF = 脑脊液。 请点击这里查看此图的较大版本.

2. 网络构建与分析

注:导航网络构建和分析的一般工作流程总结为三个主要步骤（图2）。

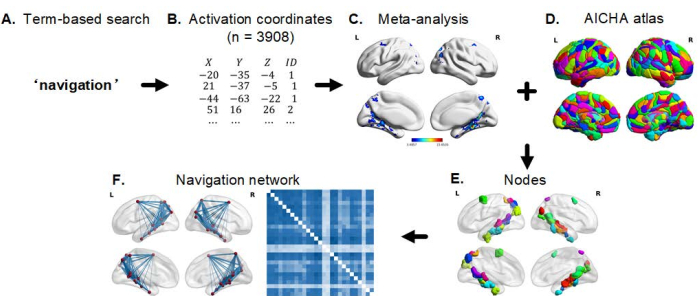
图 2:导航网络构建和分析的一般工作流程。 （A） 选择导航作为要在 Neurosynth 数据库中搜索的术语。（B） 可以生成激活坐标列表。（C） 使用 Neurosynth 中的函数运行荟萃分析，以获得多个大脑图谱。（D，E）通过结合元分析图谱和全脑包裹图谱 （AICHA），可以生成节点 （ROI）。（F） 利用由此产生的导航节点及其功能连通性构建导航网络（连通性估计和网络分析）。缩写:ROI = 感兴趣区域;AICHA = 同位素区域的内在连通性图集。 请点击这里查看此图的较大版本.

1. 网络节点定义
   1. 通过在 Python 中键入命令下载最新的 Neurosynth 数据库 （neurosynth.org）²⁰:
         
      >import neurosynth as ns
      >ns.dataset.download （path='./'， unpack = True）
         
      注意:数据集存档 （'current_data.tar.gz'） 包含两个文件:"database.txt"和"features.txt"。这些包含来自神经影像学文章和荟萃分析标签的所有激活坐标，这些标签分别在该文章中高频率出现。
   2. 从database.txt生成新的 Dataset 实例，并通过键入以下命令向这些数据添加要素:
         
      从 neurosynth.base.dataset 导入数据集>
      > 数据集 = Dataset（'data/database.txt'）
      > dataset.add_features（'数据/features.txt'）
         
   3. 通过键入以下命令，使用感兴趣的术语（即"导航"）运行荟萃分析:
         
      > ids = dataset.get_ids_by_features （'navigation'， threshold=0.01）
      > 马 = 元。MetaAnalysis（数据集，ids）
      > 马.save_results（'.'， '导航'）
         
      注意:荟萃分析得出了几张 NIFTI 格式的大脑图谱。误发现率 （FDR） 阈值为 0.01，用于控制误报率。在此步骤中需要归档知识，以确保将常见报告的区域包含在荟萃分析图中。类似的步骤可以应用于对其他认知功能（如语言和记忆）进行荟萃分析。
   4. 通过键入 FSL 中的命令，将元分析图谱和全脑包裹图谱合并，从而定义感兴趣的聚类:
         
      >fslmaths navigation_0.01.nii.gz -bin navi_bin.nii.gz
      >fslmaths navi_bin.nii.gz -mul AICHA/AAL.nii.gz navi_label_aicha/aal.nii.gz
      >fslmaths navi_label_aicha/aal.nii.gz -thr n -uthr n 标签_n.nii.gz
      >集群 -i 标签 _n.nii.gz -t 0.2 -o cluster_n.nii.gz
      >fslmaths cluster_n.nii.gz -thr m -uthr m cluster_n_m.nii.gz
      >fslmaths cluster_n_m.nii.gz -bin -mul x node_x.nii.gz
      >fslmaths node_1.nii.gz -添加 ... -添加 node_x.nii.gz navi_AICHA/AAL_mask.nii.gz
         
      注:这里使用了两个图集:AAL 和 AICHA。AAL 是原始研究中用于节点定义¹² 的图集。该图集是根据解剖剖图创建的。同位素区域内在连通性图谱 （AICHA）²¹ 具有更精细的分辨率和更高的功能同质性。我们使用每个图集定义了感兴趣的区域。
   5. 在 Python 中键入脚本以检查地图中每个区域的大小:
         
      >for i in np.arange（n）+1:
      >____region_list.附录（i）
      >____size1_list.append（np.sum（img_dat==i））
      >____size2_list.append（np.sum（aicha_img_dat==i））
      >____pct_list.append（np.sum（img_dat==i）/np.sum（aicha_img_dat==i））
         
      注意:脚本中的整数 n 表示 AICHA 和 AAL 宗地中的区域总数（分别为 384 和 128）。为了避免虚假聚类的影响，建议可以删除尺寸相对较小的聚类（例如，100 个体素）。这里使用的AICHA图集是使用功能连通性数据生成的，每个区域都显示出自身功能时间活动的同质性。
2. 网络连接估计
   注: GRETNA 工具箱用于连通性估计和网络分析。
   1. 单击" FC Matrix Construction"批次。通过选择功能数据集的路径来加载预处理的 rs-fMRI 数据。单击 静态关联 选项。将上一步获得的节点上传为图谱，计算每对区域的rs-fMRI信号的静态相关性，并将其转换为Fisher's z评分以提高正态性。
      注意: 详细操作如 图 1 所示。每个参与者的 N × N （N 表示节点数）的导航网络矩阵将以.txt格式获得。
   2. 通过以下步骤获得正加权网络，如 图 3 所示。
      1. 单击 网络分析批次。将网络矩阵添加到 "Brain Connectivity Matrix"（大脑连接矩阵 ）窗口中，然后选择一个输出目录进行准备。
      2. 对于网络配置的流水线选项，在矩阵的符号中选择正，这会将函数连接矩阵中的负连接设置为 0，并消除歧义连接²²。选择网络类型作为加权，以获取无向加权网络。
         注意:除了加权网络之外，还可以对网络进行二值化，以创建用于后续分析的二进制网络（使用不同的方法），但加权网络通常被认为具有更高的可靠性^23,24。
3. 网络分析
   1. 将小世界、全局效率、聚类系数、最短路径长度、度中心性和局部效率添加到 GRETNA 网络度量分析管道中，如图 3 所示。
      注意:小世界和全球效率是两个全球网络指标。具体而言，具有小世界的网络可以以相对较低的布线成本最大限度地提高信息传输效率。全球效率反映了运输网络中并行信息的传输效率。对于节点网络指标，度中心度衡量连接到节点的链路数。顾名思义，最短路径长度是测量集成度的基础。聚类系数表示节点的相邻节点相互关联的程度。局部效率是与节点及其邻居的通信效率（详细公式和用法在这些论文中显示）^17,25。Brain Connectivity Toolbox （BCT）²⁵ 和其他工具箱也可用于计算网络指标。
   2. 在阈值方法中选择 网络稀疏 性，排除杂散连接的混杂效应，并输入一组 阈值序列 （即此处使用 0.05、0.1、0.15、0.2、0.25、0.3、0.35、0.4、0.45、0.5 ），根据统计结果进一步确定合适的阈值。
      注: 边数与网络中最大边数与节点数样本数的比率称为稀疏性阈值。稀疏性阈值保证不同的个体具有相同数量的边。我们选择探索不同的阈值进行验证，这可以为未来研究选择最佳阈值提供有用的数据。
   3. 将随机网络编号 设置为 1,000，以使用马尔可夫布线算法²⁶ 生成随机网络。单击"运行"，在设置完所有步骤后，在 GRETNA 中运行管道。
      注意:与真正的大脑网络类似，随机网络保持相同数量的节点、边和度分布。为了确定它们是否是相当非随机的拓扑结构，将它们与大脑网络进行比较。运行管道后，将获得每个阈值的一组网络指标分数，以便进行进一步的统计分析。
   4. 通过四个步骤确定网络中的最佳模块数量。
      1. 计算平均导航网络。单击 "指标比较 "的浴池，然后选择" 连接"。加载上面获得的网络矩阵，然后选择 "平均（功能）" 操作。选择输出方向以保留平均网络矩阵;有关详细信息，请参阅 图 4 。
      2. 使用 MATLAB 中的函数 spectralcluster 将从上述步骤获得的平均网络分为 2、3、4 和 5 个模块。
      3. 使用脚本 procrustes_alignment.m 对齐模块划分后，计算 REST 1 和 REST 2 中划分为同一模块的节点比例。使用比例作为模块分区的重复性指标。
      4. 选择具有最高重复性的模块数量。
4. 统计分析
   注意:以下分析主要用于验证，在将本协议应用于个体变异研究时不需要。
   1. 检查具有不同类型节点定义策略的两个网络之间这些网络指标的相似性（即，本研究中产生的新策略称为 NaviNet_AICHA 和 Kong 等人的早期策略称为 NaviNet_AAL）¹²。使用 MATLAB 中的函数 corrcoef 计算 Pearson 相关性，并对每个稀疏性阈值重复分析。
      注意:提取网络指标后，可以进行他们感兴趣的任何统计分析。
   2. 使用 MATLAB^27,28 中的函数 ICC 检查这些网络指标的重测可靠性，该函数实现了类内相关系数的计算。
      注:原始未校正的 p 值在代表性结果部分报告。0.2 < ICC < 0.4 被解释为表示公平的重测信度，而 ICC > 0.4 被解释为中等到良好的重测信度^29,30。阴性 ICC 分数设置为零，因为阴性 ICC 的存在毫无意义且难以解释³¹.

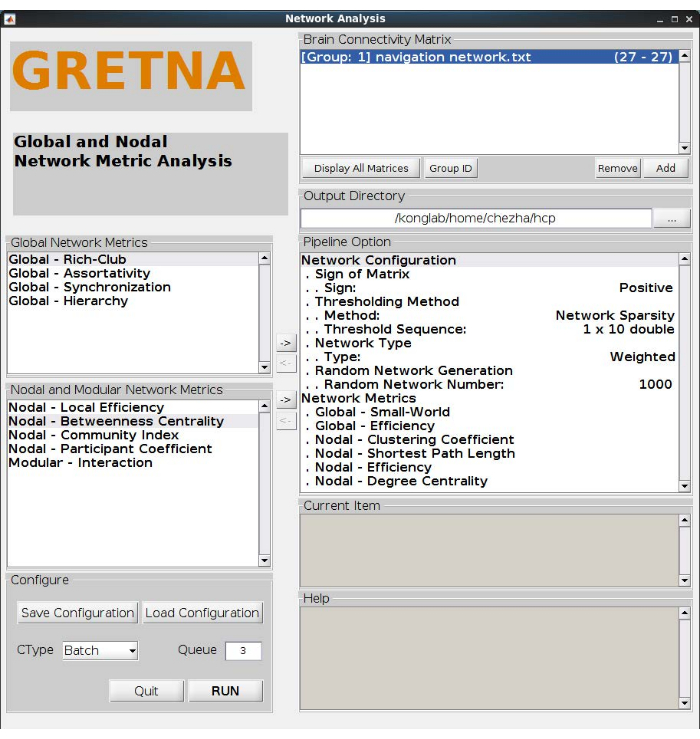
图 3:网络指标分析。 该分析定义了具有 10 个阈值的加权正网络。计算小字和效率两个全局网络度量，聚类系数、最短路径长度、效率和度中心度四个节点网络度量。 请点击这里查看此图的较大版本.

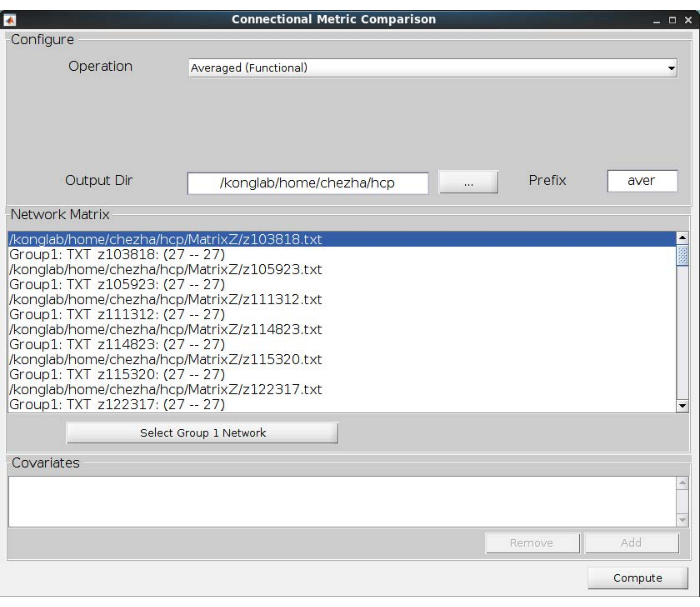
图4:平均导航网络的计算。 平均（函数）操作有助于计算所有参与者的平均网络。 请点击这里查看此图的较大版本.

结果

导航网络
本研究通过结合最新的荟萃分析神经影像数据库和 AICHA 图谱，确定了 27 个与空间导航相关的大脑区域。这些区域包括内侧颞区和顶叶区，这些区域在导航神经影像学研究中很常见。这些区域的空间分布如图5A和图5C所示。作为比较，我们还在图5B和图5D中可视化了空间导?...

讨论

网络神经科学有望帮助理解大脑网络如何支持人类认知功能³².该协议展示了一种研究人脑空间导航功能网络的综合方法，这也可以激发其他认知结构（例如语言）的网络建模。

该方法包括三个主要步骤:节点定义、网络构建和网络分析。虽然网络构建和网络分析与一般的全脑网络研究相同，但节点定义是该协议最关键的一步。此步骤利用与空间导航相关的功?...

材料

Name	Company	Catalog Number	Comments
Brain connectivity toolbox (BCT)	Mikail Rubinov & Olaf Sporns	2019	The Brain Connectivity Toolbox (brain-connectivity-toolbox.net) is a MATLAB toolbox for complex-network (graph) analysis of structural and functional brain-connectivity data sets.
GRETNA	Jinhui Wang et al.	2	GRETNA is a graph theoretical network analysis toolbox which allows researchers to perform comprehensive analysis on the topology of brain connectome by integrating the most of network measures studied in current neuroscience field.
MATLAB	MathWorks	2021a	MATLAB is a programming and numeric computing platform used by millions of engineers and scientists to analyze data, develop algorithms, and create models.
Python	Guido van Rossum et al.	3.8.6	Python is a programming language that lets you work more quickly and integrate your systems more effectively.
Statistical Parametric Mapping (SPM)	Karl Friston et.al	12	Statistical Parametric Mapping refers to the construction and assessment of spatially extended statistical processes used to test hypotheses about functional imaging data.