Modeling the Functional Network for Spatial Navigation in the Human Brain

Podsumowanie

This paper presents an integrative approach to investigating the functional network for spatial navigation in the human brain. This approach incorporates a large-scale neuroimaging meta-analytic database, resting-state functional magnetic resonance imaging, and network modeling and graph-theoretical techniques.

Streszczenie

Spatial navigation is a complex function involving the integration and manipulation of multisensory information. Using different navigation tasks, many promising results have been achieved on the specific functions of various brain regions (e.g., hippocampus, entorhinal cortex, and parahippocampal place area). Recently, it has been suggested that a non-aggregate network process involving multiple interacting brain regions may better characterize the neural basis of this complex function. This paper presents an integrative approach for constructing and analyzing the functionally-specific network for spatial navigation in the human brain. Briefly, this integrative approach consists of three major steps: 1) to identify brain regions important for spatial navigation (nodes definition); 2) to estimate functional connectivity between each pair of these regions and construct the connectivity matrix (network construction); 3) to investigate the topological properties (e.g., modularity and small worldness) of the resulting network (network analysis). The presented approach, from a network perspective, could help us better understand how our brain supports flexible navigation in complex and dynamic environments, and the revealed topological properties of the network can also provide important biomarkers for guiding early identification and diagnosis of Alzheimer's disease in clinical practice.

Wprowadzenie

Functional specificity is a fundamental organization principle of the human brain, which plays a crucial role in shaping cognitive functions¹. Abnormalities in the organization of functional specificity can reflect hallmark cognitive impairments and the associated pathological foundations of major brain disorders such as autism and Alzheimer's disease^2,3. While conventional theories and research have tended to focus on single brain regions, such as the fusiform face area (FFA) for face recognition⁴ and parahippocampus place area (PPA)⁵ for scene processing, an increasing body of evidence suggests that complex cognitive functions, including spatial navigation and language, require coordinate activity across multiple brain regions⁶. Investigating the mechanisms underlying the interactions in support of complex cognitive functions is a critical scientific question that will help to shed light on the functional architecture and operation of the brain. Here, taking spatial navigation as an example, we present an integrative method for modeling the functional network for spatial navigation in the human brain.

Spatial navigation is a complex cognitive function, which involves the integration and manipulation of multiple cognitive components, such as visual-spatial coding, memory, and decision making⁷. With functional magnetic resonance imaging (fMRI), numerous studies have made significant advances in understanding the underlying cognitive processing and neural mechanisms. For instance, specific functions have been linked to different brain regions using various navigation tasks: scene processing is specifically associated with PPA, and transformation of navigation strategies is associated with the retrosplenial cortex (RSC)^8,9. These studies provided important insights into the neural basis of spatial navigation. However, navigation is an internally dynamic and multimodal function, and the functions of single regions are not sufficient to explain large individual differences in spatial navigation¹⁰ that are commonly observed.

With the emergence of fMRI-based connectomics, researchers began to explore how some key brain regions interact with each other to support spatial navigation. For example, functional connectivity between the entorhinal and posterior cingulate cortices has been found to underpin navigation discrepancies in at-risk Alzheimer's disease¹¹. In another study, we for the first time proposed a network approach by integrating connectome methods and almost all functionally relevant regions (nodes) for spatial navigation, and the results showed that topological properties of this network showed specific associations with navigation behaviors¹². This study provides new insights into theories of how multiple brain regions interact with each other to support flexible navigation behaviors^10,13.

The present work demonstrates an updated version of the integrative approach for modeling the functional network. Briefly, two updates were included: 1) While the nodes defined in the original study were identified based on an earlier and smaller database (55 studies with 2,765 activations, accessed in 2014), the present definition was based on the latest database (77 studies with 3,908 activations, accessed in 2022); 2) to increase functional homogeneity of each node, besides the original anatomical AAL (Anatomical Automatic Labeling) atlas¹⁴, we applied a new brain parcellation, which has a much finer resolution and higher functional homogeneity (see below). We expected that both updates would improve the modeling of the functional network. This updated protocol provides a detailed procedure for investigating the neural basis of spatial navigation from a network perspective and helps understand individual variations in navigation behaviors in health and disease. A similar procedure could also be used for network modeling for other cognitive constructs (e.g., language and memory).

Protokół

NOTE: All the software used here is shown in the Table of Materials. The data used in this study for demonstration purposes were from the Human Connectome Project (HCP: http://www. humanconnectome.org)¹⁵. All experimental procedures were approved by the Institutional Review Board (IRB) at Washington University. Imaging data in the HCP dataset were acquired using a modified 3T Siemens Skyra scanner with a 32-channel head coil. Other image acquisition parameters are detailed in an earlier paper¹⁶. Minimal preprocessed data were downloaded for the demonstration, which had finished following preprocessing steps: gradient distortion correction, motion correction, field map preprocessing, spatial distortion correction, spatial normalization to the Montreal Neurological Institute (MNI) space, intensity normalization, and bias field removal. Resting-state fMRI data from researchers' projects can also be used.

1. Data preprocessing

1. Check data quality and exclude participants with missing retest data and excessive head motion (3 mm in translation and 3° in rotation).
   NOTE: Five participants were removed, and 38 young adults (22-35 years old) were included in the main analyses.
2. Open the graph theoretical network analysis (GRETNA) toolbox¹⁷ in MATLAB to perform further preprocessing steps. Click the batch of FC Matrix Construction. Select the path of the functional dataset to load the NIFTI documents and execute the following steps, as shown in the pipeline option in Figure 1:
   1. Remove the first 10 images by double-clicking Time Point Number to Remove in Remove First Images and entering 10.
   2. Spatially smooth (full width at half-maximum [FWHM] = [4 4 4] by double-clicking FWHM (mm) in Spatially Smooth and entering [4 4 4]).
   3. Regress out covariates. Choose White matter signals, CSF signals, and Head Motion as TRUE. Select the appropriate mask according to the actual voxel size, for example, mask with 2 mm here, and choose Friston-24 parameters for Head Motion.
   4. Temporally filter. Input the value of TR according to the repetition time of the MRI scan (e.g., 720 ms here) and remove high-frequency and low-frequency noise by double-clicking Band (Hz) and entering [0.01 0.1].
      NOTE: Results with and without regression of whole brain signals are presented below. When using unpreprocessed data, well-established pipelines such as fMRI-prep¹⁸ and Data Processing Assistant for Resting-State fMRI (DPARSF)¹⁹ are also recommended.

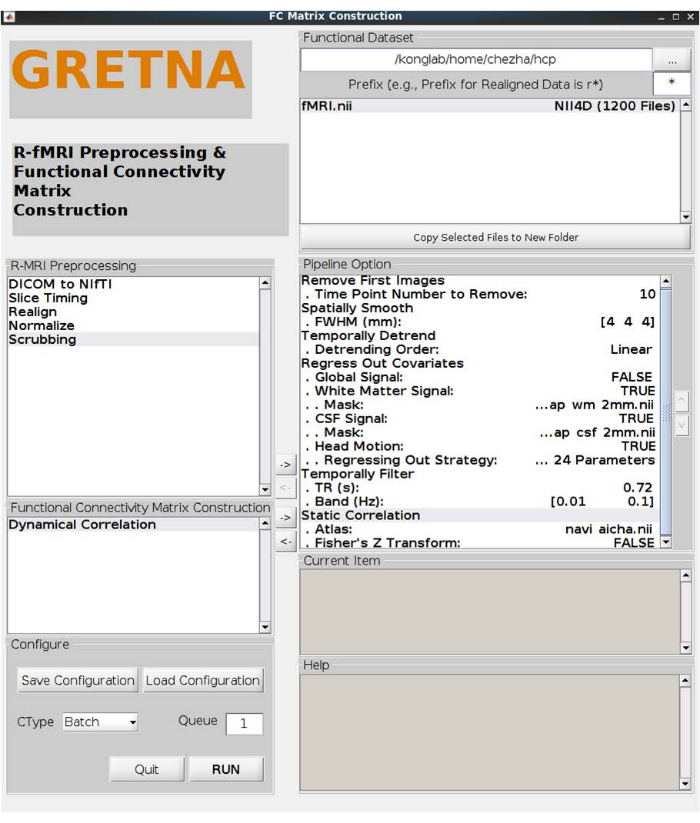
Figure 1: Rs-fMRI preprocess and functional network connectivity estimation. The settings of preprocess (removing first 10 images, spatially smoothing with FWHM of 4 mm, linear temporally detrending, regressing out white matter signals, cerebrospinal fluid (CSF) signals, and head motion with 24 parameters, filtering the band of 0.01-0.1 HZ) and the static correlation with fisher' Z transformed. Abbreviations: Rs-fMRI = resting-state functional magnetic resonance imaging; FWHM = full width at half-maximum; CSF = cerebrospinal fluid. Please click here to view a larger version of this figure.

2. Network construction and analyses

NOTE: The general workflow for the construction and analyses of the navigation network are summarized into three main steps (Figure 2).

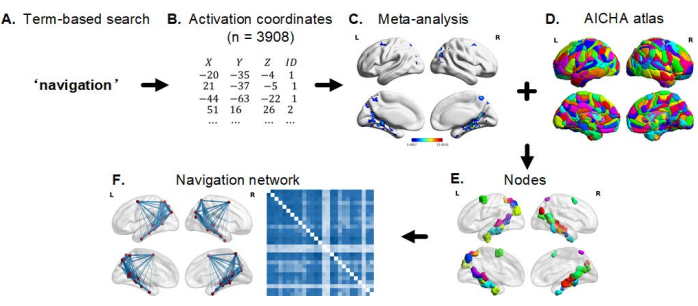
Figure 2: General workflow for the construction and analyses of the navigation network. (A) Choose navigation as the term to be searched in Neurosynth database. (B) A list of activation coordinates can be generated. (C) Run a meta-analysis using functions from the Neurosynth to get several brain maps. (D,E) By incorporating the meta-analytic map and a whole-brain parcellation atlas (AICHA), nodes (ROI) can be generated. (F) The construction of a navigation network using the resulting navigation nodes and their functional connectivity (Connectivity Estimation and Network Analysis). Abbreviations: ROI = region of interest; AICHA = atlas of intrinsic connectivity of homotopic areas. Please click here to view a larger version of this figure.

1. Network node definition
   1. Download the latest Neurosynth database (neurosynth.org)²⁰ by typing the command in Python:
         
      >import neurosynth as ns
      >ns.dataset.download (path='./', unpack = True)
         
      NOTE: The dataset archive ('current_data.tar.gz') contains two files: 'database.txt' and 'features.txt'. These contain all the activation coordinates from neuroimaging articles and meta-analysis tags that occur at a high frequency in that article, respectively.
   2. Generate a new Dataset instance from the database.txt and add featuresto these data by typing the command:
         
      > from neurosynth.base.dataset import Dataset
      > dataset = Dataset('data/database.txt')
      > dataset.add_features('data/features.txt')
         
   3. Run a meta-analysis with the term of interest (i.e., 'navigation')by typing the command:
         
      > ids = dataset.get_ids_by_features ('navigation', threshold=0.01)
      > ma = meta.MetaAnalysis (dataset, ids)
      > ma.save_results('.', 'navigation')
         
      NOTE: The meta-analysis results in several brain maps in NIFTI format. A false discovery rate (FDR) threshold of 0.01 was applied to control the false positive rate. Filed knowledge is needed at this step for ensuring that the commonly-reported regions are included in the meta-analytic map. Similar steps can be applied to run meta-analyses for other cognitive functions such as language and memory.
   4. Define clusters of interest by incorporating the meta-analytic map and a whole-brain parcellation atlas by typing the command from FSL:
         
      >fslmaths navigation_0.01.nii.gz -bin navi_bin.nii.gz
      >fslmaths navi_bin.nii.gz -mul AICHA/AAL.nii.gz navi_label_aicha/aal.nii.gz
      >fslmaths navi_label_aicha/aal.nii.gz -thr n -uthr n label _n.nii.gz
      >cluster -i label _n.nii.gz -t 0.2 -o cluster_n.nii.gz
      >fslmaths cluster_n.nii.gz -thr m -uthr m cluster_n_m.nii.gz
      >fslmaths cluster_n_m.nii.gz -bin -mul x node_x.nii.gz
      >fslmaths node_1.nii.gz -add … -add node_x.nii.gz navi_AICHA/AAL_mask.nii.gz
         
      NOTE: Two atlas were used here: AAL and AICHA. The AAL is the atlas that was used in the original study for the node definition¹². This atlas was created based on the anatomical profiles. The atlas of intrinsic connectivity of homotopic areas (AICHA)²¹ has a much finer resolution and higher functional homogeneity. We defined the regions of interest using each of the atlas.
   5. Type scripts in Python for checking the size of each region in the map:
         
      >for i in np.arange(n)+1:
      >____region_list.append(i)
      >____size1_list.append(np.sum(img_dat==i))
      >____size2_list.append(np.sum(aicha_img_dat==i))
      >____pct_list.append(np.sum(img_dat==i)/np.sum(aicha_img_dat==i))
         
      NOTE: The integer n in the script indicates the total number of regions within the AICHA and AAL parcellation (384 and 128, respectively). To avoid the effects of spurious clusters, it is suggested that clusters with relatively small sizes (e.g., 100 voxels) could be removed. The AICHA atlas used here is generated using functional connectivity data, with each region showing homogeneity of functional temporal activity within itself.
2. Network connectivity estimation
   NOTE: The GRETNA toolbox is used for connectivity estimation and network analysis.
   1. Click the batch of FC Matrix Construction. Load the preprocessed rs-fMRI data by selecting the path of the functional dataset. Click the static correlation option. Upload the node obtained in the previous step as an atlas to calculate the static correlation of rs-fMRI signals of each pair of regions and transfer them into Fisher's z scores for improving normality.
      NOTE: The detailed operation is shown in Figure 1. The navigation network matrices of N × N (N represents the number of nodes) for each participant would be obtained in .txt format.
   2. Get a positive and weighted network with the following steps, as shown in Figure 3.
      1. Click the batch of Network Analysis. Add the network matrixes into the Brain Connectivity Matrix window and choose one output directory for preparation.
      2. For the pipeline option of Network Configuration, select positive in the Sign of matrix, which will set negative connections in the function connection matrix to 0 and eliminate ambiguous connections²². Choose the network type as weighted to get the undirected weighted network.
         NOTE: Besides the weighted networks, one could also binarize the networks to create binary networks for subsequent analyses (with different approaches), but the weighted one is often considered to show higher reliability^23,24.
3. Network analysis
   1. Add small world, global efficiency, clustering coefficient, shortest path length, degree centrality, and local efficiency to the GRETNA network metric analysis pipeline, as shown in Figure 3.
      NOTE: Small world and global efficiency are two global network metrics. Specifically, the network with small-worldness can maximize the efficiency of information transfer at a comparatively low wiring cost. Global efficiency reflects the transmission efficiency parallel information in the transportation network. For nodal network metrics, the degree centrality measures the number of links connected to a node. The shortest path length, as its name, is a basis for measuring integration. The clustering coefficient indicates the degree to which the nodes' neighbors are interrelated with each other. Local efficiency is the efficiency of communication with the node and its neighbors (the detailed formula and usage are shown in these papers) ^17,25. Brain connectivity toolbox (BCT)²⁵ and other toolboxes can also be used for the calculation of the network metrics.
   2. Select Network Sparsity in the thresholding method to exclude the confounding effects of spurious connections, and enter a set of threshold sequences (i.e., 0.05, 0.1, 0.15, 0.2, 0.25, 0.3, 0.35, 0.4, 0.45, 0.5 is used here) to further determine the appropriate threshold according to the statistical results.
      NOTE: The ratio of edges to the maximum number of edges in a network with the sample number of nodes is known as the sparsity threshold. A sparsity threshold guarantees that different individuals have the same number of edges. We chose to explore different thresholds for validation, which could provide helpful data for choosing an optimal threshold in future studies.
   3. Set the random network number as 1,000 to generate random networks using a Markov wiring algorithm²⁶. Click Run to run the pipeline in GRETNA after all steps are set up.
      NOTE: Similar to genuine brain networks, the random networks maintain the same number of nodes, edges, and degree distribution. To determine whether they are considerably non-randomly topologically constructed, they will be compared to brain networks. After running the pipeline, a group of scores for the network metrics for each of the thresholds would be obtained for further statistical analyses.
   4. Determine the optimal number of modules in the network in four steps.
      1. Calculate the averaging navigation network. Click the bath of Metric Comparison and choose Connection. Load the network matrixes obtained above and choose the Averaged (Functional) operation. Select an output direction to preserve the averaged network matrix; see Figure 4 for more details.
      2. Divide the average network obtained from the above step into 2, 3, 4, and 5 modules using the function spectralcluster in MATLAB.
      3. Calculate the proportion of nodes divided into the same module in REST 1 and REST 2 after aligning the module divisions using the script procrustes_alignment.m. Use the proportion as the index of repeatability of the module partition.
      4. Select the number of modules with the highest repeatability.
4. Statistical analyses
   NOTE: The following analyses are mainly for validation and would not be necessary when applying this protocol to individual variation studies.
   1. Examine the similarity of these network metrics between two networks with different types of strategies for node definition (i.e., the new one generated in the present study, termed as NaviNet_AICHA and the earlier one from Kong et al., termed as NaviNet_AAL)¹². Calculate the Pearson correlation using the function corrcoef in MATLAB and repeat the analyses for each sparsity threshold.
      NOTE: After extracting the network metrics, one can conduct any statistical analyses they are interested in.
   2. Check the test-retest reliability of these network metrics using the function ICC in MATLAB^27,28, which implements the calculation of the Intraclass Correlation Coefficient.
      NOTE: The original uncorrected p values were reported in the representative results section. 0.2 < ICC < 0.4 is interpreted as indicative of a fair test-retest reliability and ICC > 0.4 is interpreted as moderate to good test-retest reliability^29,30. Negative ICC scores were set to zero, given the fact that the presence of negative ICCs is meaningless and difficult to interpret³¹.

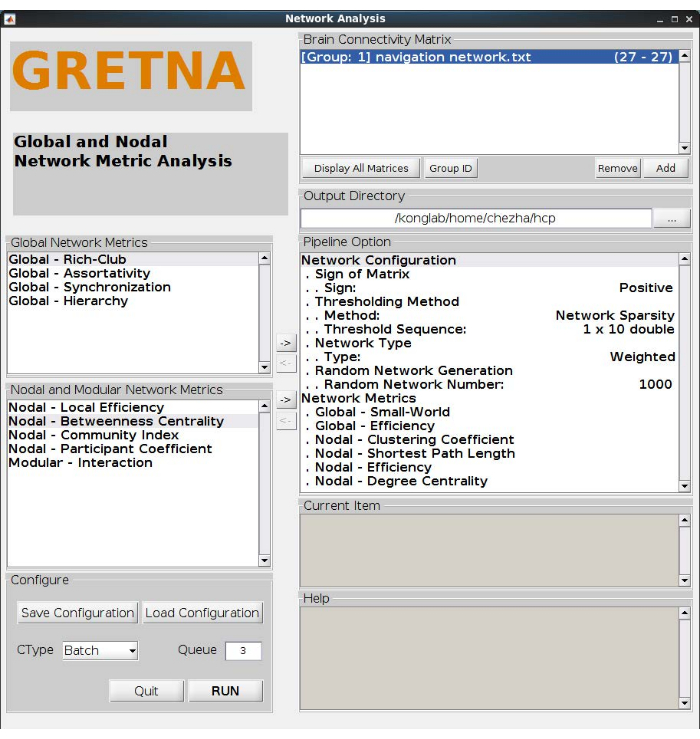
Figure 3: Network metrics analysis. This analysis defines the weighted positive networks with 10 thresholds. Calculate two global network metrics of small word and efficiency, four nodal network metrics of clustering coefficient, shortest path length, efficiency, and degree centrality. Please click here to view a larger version of this figure.

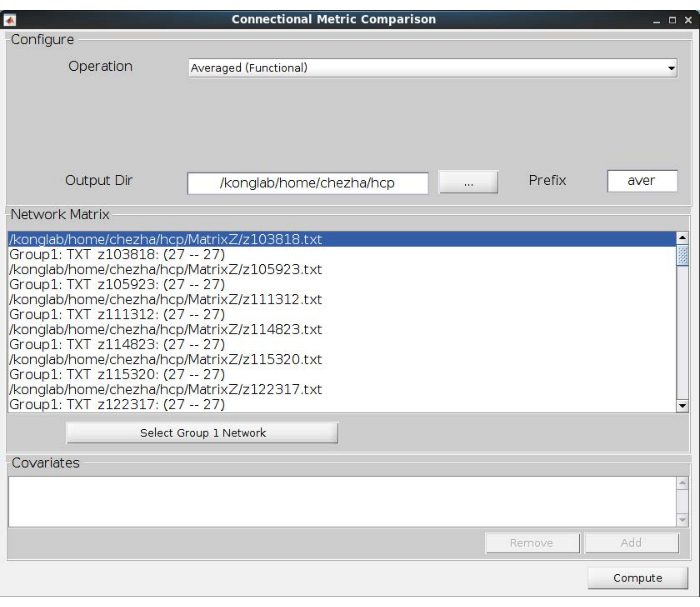
Figure 4: The calculation of average navigation networks. The averaged (functional) operation helps to calculate the average networks of all participants. Please click here to view a larger version of this figure.

Wyniki

The navigation networks
The present study identified 27 brain regions, which are associated with spatial navigation, by incorporating the latest meta-analysis neuroimaging database and the AICHA atlas. These regions consisted of the medial temporal and the parietal regions that have been commonly reported in navigation neuroimaging studies. The spatial distribution of these regions is shown in Figure 5A and Figure 5C. As a...

Dyskusje

Network neuroscience is expected to help in understanding how the brain network supports human cognitive functions³². This protocol demonstrates an integrative approach to studying the functional network for spatial navigation in the human brain, which can also inspire network modeling for other cognitive constructs (e.g., language).

This approach consisted of three main steps: node definition, network construction, and network analysis. While network construction and n...

Materiały

Name	Company	Catalog Number	Comments
Brain connectivity toolbox (BCT)	Mikail Rubinov & Olaf Sporns	2019	The Brain Connectivity Toolbox (brain-connectivity-toolbox.net) is a MATLAB toolbox for complex-network (graph) analysis of structural and functional brain-connectivity data sets.
GRETNA	Jinhui Wang et al.	2	GRETNA is a graph theoretical network analysis toolbox which allows researchers to perform comprehensive analysis on the topology of brain connectome by integrating the most of network measures studied in current neuroscience field.
MATLAB	MathWorks	2021a	MATLAB is a programming and numeric computing platform used by millions of engineers and scientists to analyze data, develop algorithms, and create models.
Python	Guido van Rossum et al.	3.8.6	Python is a programming language that lets you work more quickly and integrate your systems more effectively.
Statistical Parametric Mapping (SPM)	Karl Friston et.al	12	Statistical Parametric Mapping refers to the construction and assessment of spatially extended statistical processes used to test hypotheses about functional imaging data.