Modélisation du réseau fonctionnel pour la navigation spatiale dans le cerveau humain

Résumé

Cet article présente une approche intégrative pour étudier le réseau fonctionnel de la navigation spatiale dans le cerveau humain. Cette approche intègre une base de données méta-analytique de neuroimagerie à grande échelle, l’imagerie par résonance magnétique fonctionnelle à l’état de repos, ainsi que des techniques de modélisation de réseau et de théorie des graphes.

Résumé

La navigation spatiale est une fonction complexe impliquant l’intégration et la manipulation d’informations multisensorielles. En utilisant différentes tâches de navigation, de nombreux résultats prometteurs ont été obtenus sur les fonctions spécifiques de diverses régions du cerveau (par exemple, l’hippocampe, le cortex entorhinal et la zone parahippocampique). Récemment, il a été suggéré qu’un processus de réseau non agrégé impliquant plusieurs régions cérébrales en interaction pourrait mieux caractériser la base neuronale de cette fonction complexe. Cet article présente une approche intégrative pour la construction et l’analyse du réseau fonctionnel spécifique pour la navigation spatiale dans le cerveau humain. Brièvement, cette approche intégrative se compose de trois grandes étapes : 1) identifier les régions cérébrales importantes pour la navigation spatiale (définition des nœuds) ; 2) d’estimer la connectivité fonctionnelle entre chaque paire de ces régions et de construire la matrice de connectivité (construction du réseau) ; 3) étudier les propriétés topologiques (par exemple, la modularité et la petitesse du monde) du réseau résultant (analyse du réseau). L’approche présentée, du point de vue du réseau, pourrait nous aider à mieux comprendre comment notre cerveau supporte une navigation flexible dans des environnements complexes et dynamiques, et les propriétés topologiques révélées du réseau peuvent également fournir des biomarqueurs importants pour guider l’identification précoce et le diagnostic de la maladie d’Alzheimer dans la pratique clinique.

Introduction

La spécificité fonctionnelle est un principe d’organisation fondamental du cerveau humain, qui joue un rôle crucial dans la formation des fonctions cognitives¹. Des anomalies dans l’organisation de la spécificité fonctionnelle peuvent refléter des déficiences cognitives caractéristiques et les fondements pathologiques associés à des troubles cérébraux majeurs tels que l’autisme et la maladie d’Alzheimer ^2,3. Alors que les théories et les recherches conventionnelles ont eu tendance à se concentrer sur des régions cérébrales uniques, telles que la zone faciale fusiforme (FFA) pour la reconnaissance faciale⁴ et la zone de lieu parahippocampe (PPA)⁵ pour le traitement de la scène, un nombre croissant de preuves suggère que les fonctions cognitives complexes, y compris la navigation spatiale et le langage, nécessitent une activité coordonnée dans plusieurs régions du cerveau⁶. L’étude des mécanismes sous-jacents aux interactions à l’appui des fonctions cognitives complexes est une question scientifique cruciale qui aidera à faire la lumière sur l’architecture fonctionnelle et le fonctionnement du cerveau. Ici, en prenant l’exemple de la navigation spatiale, nous présentons une méthode intégrative pour modéliser le réseau fonctionnel de la navigation spatiale dans le cerveau humain.

La navigation spatiale est une fonction cognitive complexe, qui implique l’intégration et la manipulation de multiples composants cognitifs, tels que le codage visuo-spatial, la mémoire et la prise de décision⁷. Avec l’imagerie par résonance magnétique fonctionnelle (IRMf), de nombreuses études ont permis de réaliser des progrès significatifs dans la compréhension du traitement cognitif sous-jacent et des mécanismes neuronaux. Par exemple, des fonctions spécifiques ont été liées à différentes régions du cerveau à l’aide de diverses tâches de navigation : le traitement de la scène est spécifiquement associé à l’APP, et la transformation des stratégies de navigation est associée au cortex rétrosplénien (RSC)^8,9. Ces études ont fourni des informations importantes sur les bases neuronales de la navigation spatiale. Cependant, la navigation est une fonction intrinsèquement dynamique et multimodale, et les fonctions d’une seule région ne sont pas suffisantes pour expliquer les grandes différences individuelles dans la navigation spatiale¹⁰ qui sont couramment observées.

Avec l’émergence de la connectomique basée sur l’IRMf, les chercheurs ont commencé à explorer comment certaines régions clés du cerveau interagissent les unes avec les autres pour soutenir la navigation spatiale. Par exemple, il a été démontré que la connectivité fonctionnelle entre les cortex cingulaire entorhinal et postérieur sous-tend les divergences de navigation dans la maladie d’Alzheimer à risque¹¹. Dans une autre étude, nous avons proposé pour la première fois une approche de réseau en intégrant des méthodes de connectome et presque toutes les régions fonctionnellement pertinentes (nœuds) pour la navigation spatiale, et les résultats ont montré que les propriétés topologiques de ce réseau présentaient des associations spécifiques avec les comportements de navigation¹². Cette étude fournit de nouvelles informations sur les théories sur la façon dont plusieurs régions du cerveau interagissent les unes avec les autres pour soutenir des comportements de navigation flexibles^10,13.

Le présent travail démontre une version actualisée de l’approche intégrative pour la modélisation du réseau fonctionnel. Brièvement, deux mises à jour ont été incluses : 1) Alors que les nœuds définis dans l’étude originale ont été identifiés sur la base d’une base de données antérieure et plus petite (55 études avec 2 765 activations, consultées en 2014), la présente définition était basée sur la base de données la plus récente (77 études avec 3 908 activations, consultées en 2022) ; 2) Pour augmenter l’homogénéité fonctionnelle de chaque nœud, en plus de l’atlas anatomique AAL (Anatomical Automatic Labeling)¹⁴ original, nous avons appliqué une nouvelle parcellisation cérébrale, qui a une résolution beaucoup plus fine et une homogénéité fonctionnelle plus élevée (voir ci-dessous). Nous nous attendions à ce que les deux mises à jour améliorent la modélisation du réseau fonctionnel. Ce protocole mis à jour fournit une procédure détaillée pour étudier les bases neuronales de la navigation spatiale du point de vue du réseau et aide à comprendre les variations individuelles des comportements de navigation dans la santé et la maladie. Une procédure similaire pourrait également être utilisée pour la modélisation de réseaux pour d’autres constructions cognitives (par exemple, le langage et la mémoire).

Protocole

REMARQUE : Tous les logiciels utilisés ici sont indiqués dans le tableau des matériaux. Les données utilisées dans cette étude à des fins de démonstration proviennent du Human Connectome Project (HCP : http://www. humanconnectome.org)¹⁵. Toutes les procédures expérimentales ont été approuvées par l’Institutional Review Board (IRB) de l’Université de Washington. Les données d’imagerie de l’ensemble de données HCP ont été acquises à l’aide d’un scanner 3T Siemens Skyra modifié avec une bobine de tête à 32 canaux. D’autres paramètres d’acquisition d’images sont détaillés dans un article antérieur¹⁶. Un minimum de données prétraitées a été téléchargé pour la démonstration, qui s’est terminée en suivant les étapes de prétraitement : correction de la distorsion du gradient, correction du mouvement, prétraitement de la carte de terrain, correction de la distorsion spatiale, normalisation spatiale dans l’espace de l’Institut neurologique de Montréal (INM), normalisation de l’intensité et suppression du champ de biais. Les données d’IRMf à l’état de repos provenant de projets de chercheurs peuvent également être utilisées.

1. Prétraitement des données

1. Vérifiez la qualité des données et excluez les participants dont les données de retest sont manquantes et dont le mouvement de la tête est excessif (3 mm en translation et 3° en rotation).
   NOTE : Cinq participants ont été retirés et 38 jeunes adultes (22-35 ans) ont été inclus dans les analyses principales.
2. Ouvrez la boîte à outils GRETNA (Graph Theoretical Network Analysis)¹⁷ dans MATLAB pour effectuer d’autres étapes de prétraitement. Cliquez sur le lot de FC Matrix Construction. Sélectionnez le chemin d’accès du jeu de données fonctionnel pour charger les documents NIFTI et exécutez les étapes suivantes, comme indiqué dans l’option de pipeline de la figure 1 :
   1. Supprimez les 10 premières images en double-cliquant sur Numéro de point temporel à supprimer dans Supprimer les premières images et en saisissant 10.
   2. Lissage dans l’espace (pleine largeur à la moitié maximale [FWHM] = [4 4 4] en double-cliquant sur FWHM (mm) dans Lissage spatial et en saisissant [4 4 4]).
   3. Régresser les covariables. Choisissez White matter signals (Signaux de matière blanche), Signaux LCR (Signaux de LCR) et Head Motion (Mouvement de la tête ) sur TRUE (Vrai). Sélectionnez le masque approprié en fonction de la taille réelle du voxel, par exemple, un masque de 2 mm ici, et choisissez les paramètres Friston-24 pour Mouvement de la tête.
   4. Filtrer temporellement. Entrez la valeur de TR en fonction du temps de répétition de l’IRM (par exemple, 720 ms ici) et supprimez le bruit haute fréquence et basse fréquence en double-cliquant sur Bande (Hz) et en entrant [0.01 0.1].
      REMARQUE : Les résultats avec et sans régression des signaux du cerveau entier sont présentés ci-dessous. Lors de l’utilisation de données non prétraitées, il est également recommandé d’utiliser des pipelines bien établis tels que l’IRMf¹⁸ et l’Assistant de traitement des données pour l’IRMf à l’état de repos (DPARSF)¹⁹ .

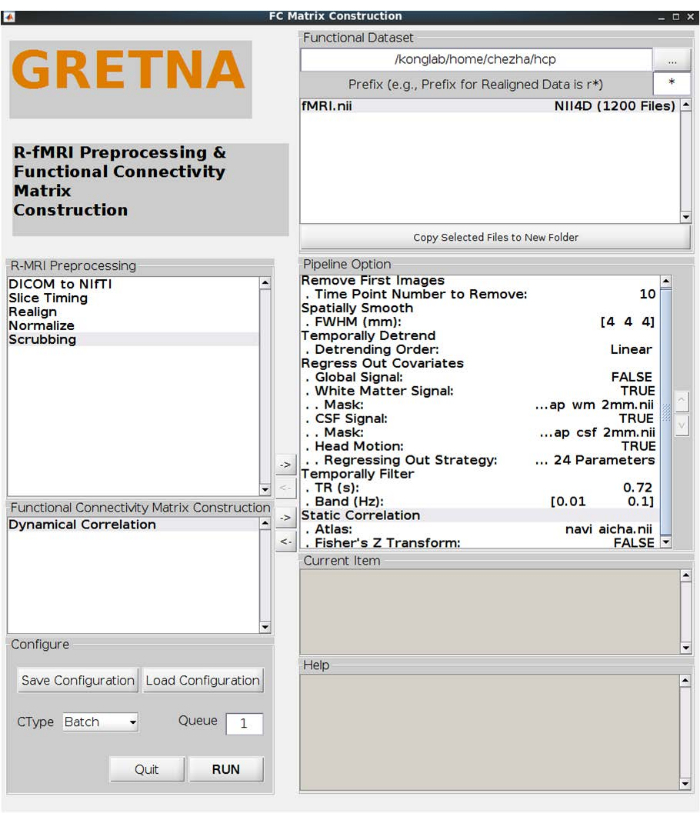
Figure 1 : Prétraitement de l’IRMf Rs-f, estimation de la connectivité fonctionnelle du réseau. Les paramètres de prétraitement (suppression des 10 premières images, lissage spatial avec FWHM de 4 mm, détendance temporelle linéaire, régression des signaux de la substance blanche, des signaux du liquide céphalorachidien (LCR) et du mouvement de la tête avec 24 paramètres, filtrage de la bande de 0,01-0,1 HZ) et la corrélation statique avec le Z de Fisher transformé. Abréviations : Rs-IRMf = imagerie par résonance magnétique fonctionnelle à l’état de repos ; FWHM = pleine largeur à mi-maximum ; LCR = liquide céphalo-rachidien. Veuillez cliquer ici pour voir une version agrandie de cette figure.

2. Construction et analyses de réseaux

NOTE : Le flux de travail général pour la construction et l’analyse du réseau de navigation est résumé en trois étapes principales (Figure 2).

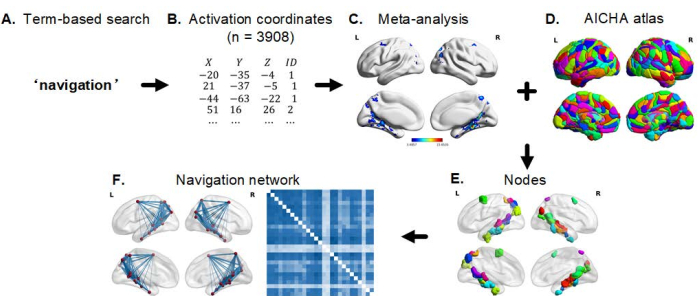
Figure 2 : Flux de travail général pour la construction et l’analyse du réseau de navigation. (A) Choisissez la navigation comme terme à rechercher dans la base de données Neurosynth. (B) Une liste de coordonnées d’activation peut être générée. (C) Exécutez une méta-analyse en utilisant les fonctions du Neurosynth pour obtenir plusieurs cartes cérébrales. (D,E) En incorporant la carte méta-analytique et un atlas de parcellation du cerveau entier (AICHA), des nœuds (ROI) peuvent être générés. (F) La construction d’un réseau de navigation à l’aide des nœuds de navigation qui en résultent et de leur connectivité fonctionnelle (estimation de la connectivité et analyse du réseau). Abréviations : ROI = région d’intérêt ; AICHA = atlas de la connectivité intrinsèque des aires homotopiques. Veuillez cliquer ici pour voir une version agrandie de cette figure.

1. Définition du noeud de réseau
   1. Téléchargez la dernière base de données Neurosynth (neurosynth.org)²⁰ en tapant la commande en Python :
         
      >importer un neurosynthé en tant que ns
      >ns.dataset.download (chemin = './', unpack = True)
         
      REMARQUE : L’archive du jeu de données ('current_data.tar.gz') contient deux fichiers : 'database.txt' et 'features.txt'. Ceux-ci contiennent toutes les coordonnées d’activation des articles de neuroimagerie et des balises de méta-analyse qui se produisent à une fréquence élevée dans cet article, respectivement.
   2. Générez une nouvelle instance de jeu de données à partir de la database.txt et ajoutez des entités à ces données en tapant la commande :
         
      > à partir de neurosynth.base.dataset import Jeu de données
      > dataset = Jeu de données('données/database.txt')
      > dataset.add_features('données/features.txt')
         
   3. Exécutez une méta-analyse avec le terme d’intérêt (c’est-à-dire 'navigation') en tapant la commande :
         
      > ids = dataset.get_ids_by_features ('navigation', threshold=0.01)
      > ma = méta. Méta-analyse (jeu de données, ids)
      > ma.save_results('.', 'navigation')
         
      REMARQUE : La méta-analyse donne lieu à plusieurs cartes cérébrales au format NIFTI. Un seuil de taux de fausses découvertes (FDR) de 0,01 a été appliqué pour contrôler le taux de faux positifs. Des connaissances classées sont nécessaires à cette étape pour s’assurer que les régions couramment déclarées sont incluses dans la carte méta-analytique. Des étapes similaires peuvent être appliquées pour effectuer des méta-analyses pour d’autres fonctions cognitives telles que le langage et la mémoire.
   4. Définissez les groupes d’intérêt en incorporant la carte méta-analytique et un atlas de parcellisation du cerveau entier en tapant la commande de FSL :
         
      >fslmaths navigation_0.01.nii.gz -bin navi_bin.nii.gz
      >fslmaths navi_bin.nii.gz -mul AICHA/AAL.nii.gz navi_label_aicha/aal.nii.gz
      >fslmaths navi_label_aicha/aal.nii.gz -thr n -uthr n label _n.nii.gz
      >cluster -i label _n.nii.gz -t 0.2 -o cluster_n.nii.gz
      >fslmaths cluster_n.nii.gz -thr m -uthr m cluster_n_m.nii.gz
      >fslmaths cluster_n_m.nii.gz -bin -mul x node_x.nii.gz
      >fslmaths node_1.nii.gz -add ... -add node_x.nii.gz navi_AICHA/AAL_mask.nii.gz
         
      NOTE : Deux atlas ont été utilisés ici : AAL et AICHA. L’AAL est l’atlas qui a été utilisé dans l’étude originale pour la définition du nœud¹². Cet atlas a été créé sur la base des profils anatomiques. L’atlas de la connectivité intrinsèque des aires homotopiques (AICHA)²¹ a une résolution beaucoup plus fine et une homogénéité fonctionnelle plus élevée. Nous avons défini les régions d’intérêt à l’aide de chacun des atlas.
   5. Tapez des scripts en Python pour vérifier la taille de chaque région de la carte :
         
      >pour i dans np.arange(n)+1 :
      >____region_list.Ajouter(i)
      >____size1_list.append(np.sum(img_dat==i))
      >____size2_list.append(np.sum(aicha_img_dat==i))
      >____pct_list.append(np.sum(img_dat==i)/np.sum(aicha_img_dat==i))
         
      REMARQUE : L’entier n dans le script indique le nombre total de régions dans la parcellation AICHA et AAL (384 et 128, respectivement). Pour éviter les effets des amas parasites, il est suggéré d’enlever les amas de taille relativement petite (p. ex., 100 voxels). L’atlas AICHA utilisé ici est généré à l’aide de données de connectivité fonctionnelle, chaque région montrant l’homogénéité de l’activité temporelle fonctionnelle en son sein.
2. Estimation de la connectivité réseau
   REMARQUE : La boîte à outils GRETNA est utilisée pour l’estimation de la connectivité et l’analyse du réseau.
   1. Cliquez sur le lot de FC Matrix Construction. Chargez les données rs-fMRI prétraitées en sélectionnant le chemin d’accès au jeu de données fonctionnel. Cliquez sur l’option de corrélation statique . Téléchargez le nœud obtenu à l’étape précédente sous forme d’atlas pour calculer la corrélation statique des signaux rs-IRMf de chaque paire de régions et transférez-les dans les scores z de Fisher pour améliorer la normalité.
      REMARQUE : Le fonctionnement détaillé est illustré à la Figure 1. Les matrices du réseau de navigation de N × N (N représente le nombre de nœuds) pour chaque participant seraient obtenues dans .txt format.
   2. Obtenez un réseau positif et pondéré en procédant comme suit, comme illustré à la figure 3.
      1. Cliquez sur le lot d’analyse de réseau. Ajoutez les matrices de réseau dans la fenêtre Matrice de connectivité cérébrale et choisissez un répertoire de sortie pour la préparation.
      2. Pour l’option de pipeline de Configuration réseau, sélectionnez positif dans la matrice Signe de, ce qui définira les connexions négatives dans la matrice de connexion de fonction sur 0 et éliminera les connexions ambiguës²². Choisissez le type de réseau pondéré pour obtenir le réseau pondéré non dirigé.
         NOTE : Outre les réseaux pondérés, on peut également binariser les réseaux pour créer des réseaux binaires pour des analyses ultérieures (avec des approches différentes), mais le réseau pondéré est souvent considéré comme présentant une plus grande fiabilité^23,24.
3. Analyse de réseau
   1. Ajoutez le petit monde, l’efficacité globale, le coefficient de clustering, la longueur de chemin la plus courte, la centralité du degré et l’efficacité locale au pipeline d’analyse des métriques du réseau GRETNA, comme illustré à la figure 3.
      REMARQUE : Le petit monde et l’efficacité globale sont deux mesures de réseau globales. Plus précisément, le réseau à petite échelle peut maximiser l’efficacité du transfert d’informations à un coût de câblage relativement faible. L’efficacité globale reflète l’information parallèle sur l’efficacité de la transmission dans le réseau de transport. Pour les métriques de réseau nodal, le degré de centralité mesure le nombre de liaisons connectées à un nœud. La longueur de chemin la plus courte, comme son nom l’indique, est une base pour mesurer l’intégration. Le coefficient d’agrégation indique le degré d’interdépendance entre les nœuds voisins. L’efficacité locale est l’efficacité de la communication avec le nœud et ses voisins (la formule détaillée et l’utilisation sont présentées dans ces articles) ^17,25. Brain connectivity toolbox (BCT)²⁵ et d’autres toolboxes peuvent également être utilisés pour le calcul des métriques du réseau.
   2. Sélectionnez Parcimonie du réseau dans la méthode de seuillage pour exclure les effets de confusion des connexions parasites, puis entrez un ensemble de séquences de seuils (c’est-à-dire 0,05, 0,1, 0,15, 0,2, 0,25, 0,3, 0,35, 0,4, 0,45, 0,5 est utilisé ici) pour déterminer davantage le seuil approprié en fonction des résultats statistiques.
      REMARQUE : Le rapport entre le nombre de tronçons et le nombre maximal de tronçons dans un réseau avec le nombre d’échantillons de nœuds est connu sous le nom de seuil de parcimonie. Un seuil de parcimonie garantit que différents individus ont le même nombre d’arêtes. Nous avons choisi d’explorer différents seuils de validation, ce qui pourrait fournir des données utiles pour choisir un seuil optimal dans les études futures.
   3. Définissez le numéro de réseau aléatoire sur 1 000 pour générer des réseaux aléatoires à l’aide d’un algorithme de câblage de Markov²⁶. Cliquez sur Exécuter pour exécuter le pipeline dans GRETNA une fois toutes les étapes configurées.
      REMARQUE : Similaires aux véritables réseaux cérébraux, les réseaux aléatoires conservent le même nombre de nœuds, d’arêtes et la même distribution de degrés. Pour déterminer s’ils sont construits topologiquement de manière non aléatoire, ils seront comparés à des réseaux cérébraux. Après l’exécution du pipeline, un groupe de scores pour les métriques réseau pour chacun des seuils serait obtenu pour d’autres analyses statistiques.
   4. Déterminez le nombre optimal de modules dans le réseau en quatre étapes.
      1. Calculez la moyenne du réseau de navigation. Cliquez sur le bain de Comparaison de métriques et choisissez Connexion. Chargez les matrices de réseau obtenues ci-dessus et choisissez l’opération Moyenne (fonctionnelle). Sélectionnez une direction de sortie pour conserver la matrice de réseau moyennée ; voir la figure 4 pour plus de détails.
      2. Divisez le réseau moyen obtenu à partir de l’étape ci-dessus en 2, 3, 4 et 5 modules à l’aide de la fonction spectralcluster dans MATLAB.
      3. Calculez la proportion de noeuds divisés dans le même module dans REST 1 et REST 2 après avoir aligné les divisions de module à l’aide du script procrustes_alignment.m. Utilisez la proportion comme indice de répétabilité de la partition de module.
      4. Sélectionnez le nombre de modules avec la répétabilité la plus élevée.
4. Analyses statistiques
   NOTA : Les analyses suivantes sont principalement destinées à la validation et ne seraient pas nécessaires lors de l’application de ce protocole à des études de variation individuelles.
   1. Examinez la similitude de ces métriques de réseau entre deux réseaux ayant des types différents de stratégies pour la définition des nœuds (c’est-à-dire la nouvelle générée dans la présente étude, appelée NaviNet_AICHA et la précédente de Kong et al., appelée NaviNet_AAL)¹². Calculez la corrélation de Pearson à l’aide de la fonction corrcoef dans MATLAB et répétez les analyses pour chaque seuil de parcimonie.
      REMARQUE : Après avoir extrait les métriques du réseau, on peut effectuer toutes les analyses statistiques qui l’intéressent.
   2. Vérifiez la fiabilité test-retest de ces métriques réseau à l’aide de la fonction ICC dans MATLAB^27,28, qui implémente le calcul du coefficient de corrélation intraclasse.
      NOTA : Les valeurs p originales non corrigées ont été rapportées dans la section des résultats représentatifs. 0,2 < ICC < 0,4 est interprété comme indiquant une fiabilité test-retest passable et ICC > 0,4 est interprété comme une fiabilité test-retest modérée à bonne^29,30. Les scores négatifs de l’ICC ont été mis à zéro, étant donné que la présence d’ICC négatifs n’a pas de sens et est difficile à interpréter³¹.

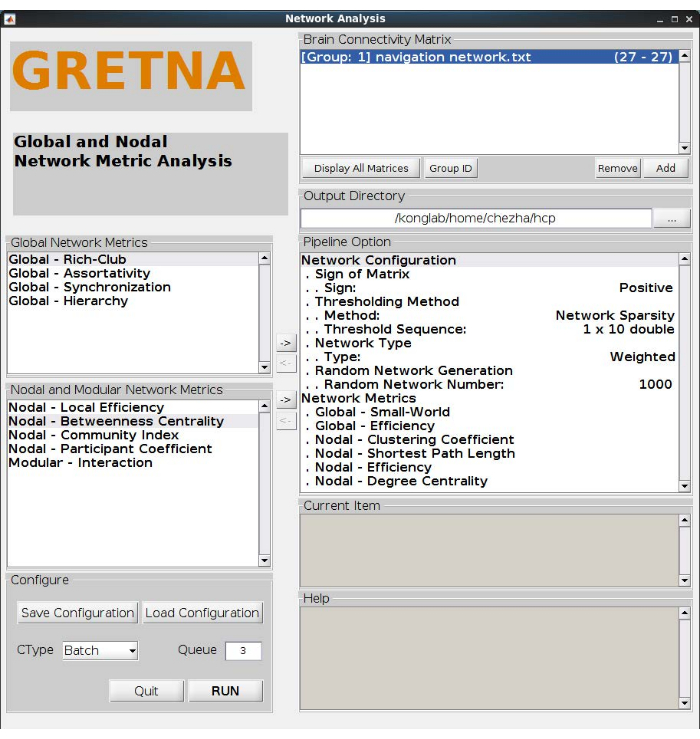
Figure 3 : Analyse des métriques du réseau. Cette analyse définit les réseaux positifs pondérés avec 10 seuils. Calculez deux mesures de réseau global de mots petits et d’efficacité, quatre mesures de réseau nodal de coefficient de clustering, de longueur de chemin le plus court, d’efficacité et de degré de centralité. Veuillez cliquer ici pour voir une version agrandie de cette figure.

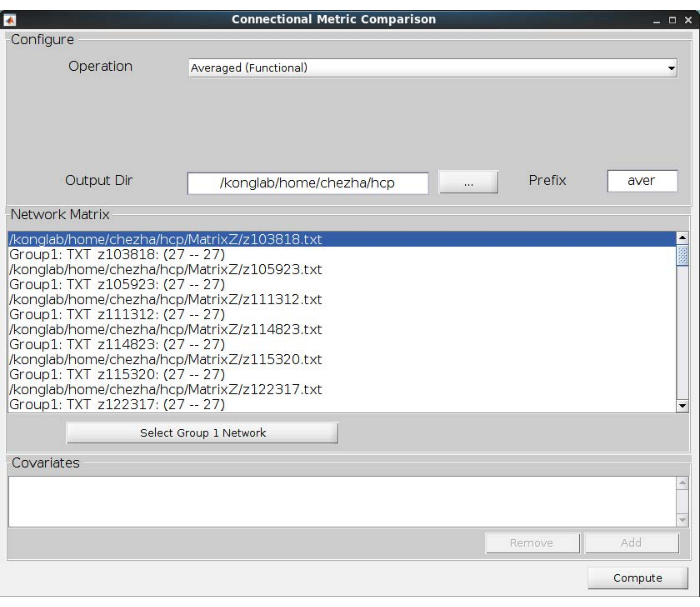
Figure 4 : Calcul de la moyenne des réseaux de navigation. L’opération moyenne (fonctionnelle) permet de calculer les réseaux moyens de tous les participants. Veuillez cliquer ici pour voir une version agrandie de cette figure.

Résultats

Les réseaux de navigation
La présente étude a identifié 27 régions du cerveau, qui sont associées à la navigation spatiale, en incorporant la dernière base de données de neuroimagerie de méta-analyse et l’atlas AICHA. Ces régions étaient constituées des régions temporales médiales et pariétales qui ont été couramment rapportées dans les études de neuroimagerie de navigation. La répartition spatiale de ces régions est illustrée à la figure 5A et ?...

Discussion

On s’attend à ce que les neurosciences des réseaux aident à comprendre comment le réseau cérébral soutient les fonctions cognitives humaines³². Ce protocole démontre une approche intégrative de l’étude du réseau fonctionnel pour la navigation spatiale dans le cerveau humain, ce qui peut également inspirer la modélisation de réseau pour d’autres constructions cognitives (par exemple, le langage).

Cette approche se composait de trois étapes principales...

matériels

Name	Company	Catalog Number	Comments
Brain connectivity toolbox (BCT)	Mikail Rubinov & Olaf Sporns	2019	The Brain Connectivity Toolbox (brain-connectivity-toolbox.net) is a MATLAB toolbox for complex-network (graph) analysis of structural and functional brain-connectivity data sets.
GRETNA	Jinhui Wang et al.	2	GRETNA is a graph theoretical network analysis toolbox which allows researchers to perform comprehensive analysis on the topology of brain connectome by integrating the most of network measures studied in current neuroscience field.
MATLAB	MathWorks	2021a	MATLAB is a programming and numeric computing platform used by millions of engineers and scientists to analyze data, develop algorithms, and create models.
Python	Guido van Rossum et al.	3.8.6	Python is a programming language that lets you work more quickly and integrate your systems more effectively.
Statistical Parametric Mapping (SPM)	Karl Friston et.al	12	Statistical Parametric Mapping refers to the construction and assessment of spatially extended statistical processes used to test hypotheses about functional imaging data.