动量守恒

动量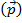定义为物体时间为其速度的质量:

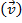.（方程 1）

此外可以定义对象 （牛顿第二定律） 力推动:

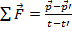.（公式 2）

在这里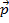，是最初的动力和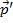是最后的势头，与相同的约定时间用于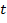和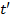。对象的作用力的总和等于物体的动量随时间变化。因此，如果对象没有净力，动量的变化将为零。说另一种方式，在一个封闭的系统与不受外力作用，最初的动力将等于最后的势头。

这一概念是最容易理解的一维、 二维碰撞。在一维碰撞，物体都有重量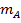和初始速度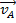碰撞与另一个物体都有重量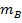和初始速度。在这些碰撞，将假定外部力量为太小了，有效果。在实验室中，气垫导轨用来减少摩擦，外力的作用，对滑翔飞行的鸟类。如果最初的动力是等于最后的势头，那么:

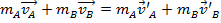（公式 3）

在那里引物的速度代表最后的流速与非底层的之间代表初始速度。

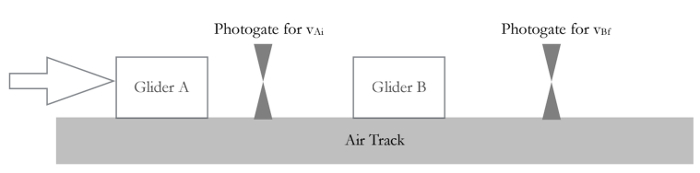
图 1.实验设置。

表 1。从两个滑翔机的质量相等的结果。

滑翔机 （试行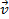）	(cm/s)	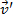(cm/s)	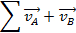(cm/s)	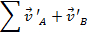(cm/s)	差异 (%)
(1)	72.5	-0.2	-	-	-
B (1)	0.0	67.1	72.5	66.9	8
A （2）。	35.6	0.3	-	-	-
B (2)	0.0	37.4	35.6	37.7	6
(3)	47.4	0.0	-	-	-
B (3)	0.0	47.8	47.4	47.8	1

表 2。结果从两个滑翔机的不同的质量。

滑翔机 （试行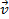）	(cm/s)	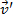(cm/s)	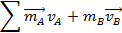(公斤厘米/s)	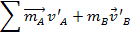(公斤厘米/s)	差异 (%)
(1)	52.9	-10.7	-	-	-
B (1)	0.0	37.7	52.9	64.7	22
A （2）。	60.2	-13.2	-	-	-
B (2)	0.0	41.5	60.2	69.8	16
(3)	66.2	-12.0	-	-	-
B (3)	0.0	45.9	66.2	79.7	20

表 3。从不从休息的质量相等的结果。

滑翔机 （试行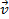）	(cm/s)	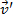(cm/s)	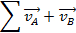(cm/s)	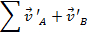(cm/s)	差异 (%)
(1)	48.8	-29.9	-	-	-
B (1)	-42.4	39.8	6.4	9.9	55
A （2）。	38.6	-25.2	-	-	-
B (2)	-33.4	32.8	5.2	7.6	46
(3)	38.9	-43.1	-	-	-
B (3)	-48.5	36.3	-9.6	-6.8	41

步骤 2、 3 和 4 的结果确认方程 3所作的预测。在步骤 2 中，滑翔机 A 来到后相撞滑翔机 B.几乎完全停止因此，几乎所有其动量传输到滑翔机 B.在步骤 3 中，滑翔机 A 不到站下车后与重滑翔机 B.相撞相反，它返回后传授一些动力滑翔机 B.向相反的方向在步骤 4 中，系统的总动量保持不变，尽管这两个滑翔机的方向变化。事实上，在某些情况下，总动量似乎会增加两个滑翔机下降的速度是与事实有关，那里是实验误差和碰撞本身并非完全弹性。声音和碰撞的废热可以采取系统的能量。这一事实，气垫导轨可能不是完全水平可以改变的速度滑翔飞行的鸟类的行为。如果甚至略微倾斜的轨道，速度会增加，由于重力的方向。结果还表明，系统，无论初始速度的总动量保持不变。

没有动量守恒，火箭将永远不会离开地面。火箭不实际上反对任何推-他们依靠推力起飞。最初，火箭和火箭本身的燃料都一动不动，和有动量为零。启动时，火箭推进了乏的燃料非常迅速。这乏的燃料的质量和动量。如果最后的势头必须等于最初的势头 （零），然后在相反的方向的废弃燃料必须有一些势头。因此，火箭是向上推进。

曾经开了一枪的人理解动量守恒。火箭的燃料系统从上面，像枪/弹药系统也开始在休息。当弹药发射出枪以惊人的速度时，在相反的方向来抵消子弹的势头必须有一些势头。这被称为反冲，并且可以是非常强大的。

由几个金属球，悬挂在字符串组成的流行桌装饰称为"牛顿摇篮"很好的理由。这是动量的另一个例子守恒。当一个球是解除和释放时，看来它的邻居，转移其势头。这一势头沿着线直到最后球第一，使其向外凸出的发展势头。这会走下去，如果不是因为外部力量，如空气阻力及能量损失的碰撞。

在这个实验中，通过考虑碰撞的两个滑翔机附近无摩擦的轨道上验证了动量守恒定律的法律。这个基本的法律也许是最重要的因为它能解决问题。如果有人知道初始动量，然后她知道最终的动量，反之亦然。