Conservação do Momento

Fonte: Nicholas Timmons, Asantha Cooray, PhD, Departamento de Física & Astronomia, Escola de Ciências Físicas, Universidade da Califórnia, Irvine, CA

O objetivo deste experimento é testar o conceito de conservação do momento. Ao configurar uma superfície com muito pouco atrito, colisões entre objetos em movimento podem ser estudadas, incluindo seu momento inicial e final.

A conservação do impulso é uma das leis mais importantes da física. Quando algo é conservado na física, o valor inicial é igual ao valor final. Para o momento, isso significa que o impulso inicial total de um sistema será igual ao momento final total. A segunda lei de Newton diz que a força em um objeto será igual à mudança no momento do objeto com o tempo. Este fato, combinado com a ideia de que o impulso é conservado, sustenta o funcionamento da mecânica clássica e é uma poderosa ferramenta de resolução de problemas.

O 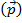momento é definido como a massa de um objeto vezes sua 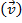velocidade:

. (Equação 1)

Pode-se também definir o impulso em termos das forças que agem sobre um objeto (segunda lei de Newton):

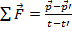. (Equação 2)

Aqui, 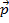é o momento inicial e é o momento 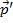final, com a mesma convenção usada para o tempo 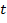e 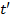. A soma das forças que agem sobre um objeto é igual à mudança no momento do objeto com o tempo. Portanto, se não houver força líquida agindo sobre um objeto, a mudança no momento será zero. Dito de outra forma, em um sistema fechado sem forças externas, o impulso inicial será igual ao momento final.

Este conceito é mais facilmente compreendido no contexto de colisões unidimensionais e bidimensionais. Em colisões unidimensionais, um objeto com massa 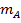e velocidade inicial 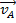colide com outro objeto com massa 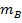e velocidade inicial. Nessas colisões, as forças externas serão consideradas muito pequenas para ter um efeito. No laboratório, uma pista de ar é usada para reduzir a quantidade de atrito, uma força externa, nos planadores. Se o momento inicial é igual ao momento final, então:

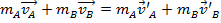, (Equação 3)

onde as velocidades preparadas representam que as velocidades finais e as velocidades não primidas representam as velocidades iniciais.

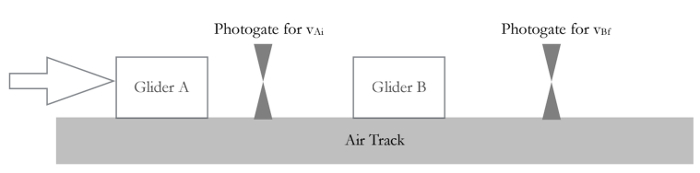
Figura 1. Configuração experimental.

1. Entendendo o temporizador do fotogate.

1. Usando um equilíbrio, meça e grave a massa de cada planador.
2. Coloque um planador na pista com um temporizador de fotogate.
3. Ajuste o temporizador do photogate para a configuração "portão".
4. Quando o planador passar pelo fotogate, ele registrará o tempo em que a bandeira acima do planador passa pelo portão. Em uma viagem de volta, o photogate não exibirá um novo tempo. Alterne o alternador para "ler" para que ele exiba o tempo inicial mais a hora da segunda passagem pelo portão.
5. A bandeira tem 10 cm de comprimento; determinar a velocidade do planador usando o fato de que a velocidade é a distância dividida pelo tempo.
6. Envie o planador através do fotogate várias vezes, incluindo as viagens de retorno depois que ele saltou da parede distante, e meça as velocidades a fim de se familiarizar com o equipamento. Lembre-se que a velocidade tem uma direção. Que a direção de velocidade inicial represente positivo e a direção oposta represente valores de velocidade negativos.

2. Dois planadores de massa igual.

1. Coloque dois planadores e dois temporizadores de fotogate na pista, como na Figura 1.
2. Use a Equação 3 para determinar a expressão para as velocidades finais. Nesta parte do experimento, o planador B começará de repouso.
3. Dê ao planador A alguma velocidade inicial para que ele colida com o planador B. Regisse a velocidade inicial do planador A, bem como as velocidades finais de cada planador. Faça isso três vezes, registe seus resultados e compare-os com a previsão teórica.

3. Dois planadores de massa desigual.

1. Adicione 4 pesos ao planador B, que dobrará sua massa. Repita as etapas 2.1-2.3.

4. Massas iguais não começam do repouso

1. Remova os pesos do planador B.
2. Repita as etapas 2.1-2.3, mas dê ao planador B uma velocidade inicial também, na direção do planador A.

Mesa 1. Resultados de dois planadores de massa igual.

Planador (julgamento)	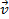(cm/s)	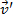(cm/s)	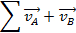(cm/s)	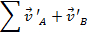(cm/s)	Diferença (%)
A (1)	72.5	-0.2	-	-	-
B (1)	0.0	67.1	72.5	66.9	8
A (2)	35.6	0.3	-	-	-
B (2)	0.0	37.4	35.6	37.7	6
A (3)	47.4	0.0	-	-	-
B (3)	0.0	47.8	47.4	47.8	1

Mesa 2. Resultados de dois planadores de massa desigual.

Planador (julgamento)	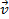(cm/s)	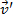(cm/s)	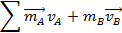(kg cm/s)	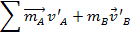(kg cm/s)	Diferença (%)
A (1)	52.9	-10.7	-	-	-
B (1)	0.0	37.7	52.9	64.7	22
A (2)	60.2	-13.2	-	-	-
B (2)	0.0	41.5	60.2	69.8	16
A (3)	66.2	-12.0	-	-	-
B (3)	0.0	45.9	66.2	79.7	20

Mesa 3. Resultados de massas iguais que não começam do repouso.

Planador (julgamento)	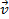(cm/s)	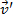(cm/s)	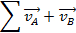(cm/s)	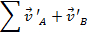(cm/s)	Diferença (%)
A (1)	48.8	-29.9	-	-	-
B (1)	-42.4	39.8	6.4	9.9	55
A (2)	38.6	-25.2	-	-	-
B (2)	-33.4	32.8	5.2	7.6	46
A (3)	38.9	-43.1	-	-	-
B (3)	-48.5	36.3	-9.6	-6.8	41

Os resultados das etapas 2, 3 e 4 confirmam as previsões feitas pela Equação 3. Na etapa 2, o planador A chega a uma parada quase completa depois de colidir com o planador B. Portanto, quase todo o seu impulso é transferido para o planador B. Na etapa 3, o planador A não para depois de colidir com o planador B mais pesado. Em vez disso, ele retorna na direção oposta depois de transmitir algum impulso ao planador B. Na etapa 4, o impulso total do sistema permanece o mesmo, apesar das mudanças de direção de ambos os planadores. O fato de que, em alguns casos, o impulso total parece aumentar e as velocidades de ambos os planadores diminuem está relacionado ao fato de que há erro experimental e as colisões em si não são completamente elásticas. Som e calor devidos pelas colisões podem tirar energia do sistema. O fato de que a pista aérea pode não estar totalmente nivelada pode mudar o comportamento das velocidades dos planadores. Se a pista estiver ligeiramente inclinada, as velocidades aumentarão nessa direção devido à gravidade. Os resultados ainda mostram que o impulso total do sistema, independentemente das velocidades iniciais, permanece constante.

Sem a conservação do impulso, os foguetes nunca sairiam do solo. Foguetes não empurram contra nada - eles dependem de impulso para decolar. Inicialmente, o combustível de um foguete e o foguete em si estão imóveis e não têm impulso. Ao lançar, o foguete impulsiona o combustível gasto muito rapidamente. Este combustível gasto tem massa e impulso. Se o momento final deve ser igual ao momento inicial (zero), então deve haver algum impulso na direção oposta do combustível descartado. Assim, o foguete é impulsionado para cima.

Qualquer um que já disparou uma arma entende a conservação do momento. Como o sistema de foguetes/combustível de cima, o sistema de armas/munições também começa em repouso. Quando a munição é disparada para fora da arma a uma velocidade tremenda, deve haver algum impulso na direção oposta para cancelar o impulso da bala em alta velocidade. Isso é conhecido como recuo e pode ser muito poderoso.

O ornamento de mesa popular que consiste em várias bolas de metal penduradas em cordas é chamado de "berço de Newton" por uma boa razão. É outro exemplo da conservação do momento. Quando uma bola é levantada e liberada, ela atinge seu vizinho, transferindo seu ímpeto. O ímpeto desce a linha até que a bola final tenha o impulso do primeiro, fazendo com que ela gire para fora. Isso continuaria para sempre se não fosse por forças externas, como resistência ao ar e perda de energia devido às colisões.

Neste experimento, a lei de conservação do momento foi verificada considerando a colisão de dois planadores em uma pista quase sem atrito. Esta lei fundamental é talvez mais importante devido ao seu poder de resolver problemas. Se alguém sabe o momento inicial, então ela sabe o momento final, e vice-versa.