胡克的法律和简谐运动
Overview
资料来源: Ketron 米切尔韦恩博士, Asantha 库雷博士,物理系 & 天文,物理科学学院,加利福尼亚大学,加利福尼亚州欧文市
势能是物理学的一个重要概念。势能是与力量,取决于对象相对于其周围环境的位置相关联。重力势能,讨论在另一段视频,是相关联的能量,是对象地面以上的高度成正比。同样,也可以定义弹簧势能,它是春天的位移从放松的状态直接成正比。拉伸或压缩弹簧有潜在的能量,因为它有能力来做工作的对象。"能够做的工作"是经常引述能源的基本定义。
这个视频将展示存储在弹簧中的势能。它还将核查弹簧,或者胡克定律的恢复力方程。不同弹性的弹簧,弹簧常数是不同的。将验证胡克定律和弹簧常数测定附着一个悬浮的弹簧在不同的权重和测量结构的位移。
Principles
举行春季或者其压缩或拉伸的位置需要某人或某物在弹簧上施加一个力。这支部队是春天的位移,而主峰,成正比。反过来,弹簧产生一个相同大小的力:
F = -k Δy,(方程 1)
在哪里k称为"弹簧刚度常数"。这是通常称为"恢复力"因为弹簧作用力方向相反的位移,负号表示。方程 1被称为胡克定律。
简谐运动将发生时是位移成正比的平衡,正如在胡克定律的恢复力。从牛顿第二定律, F = ma,并认识到加速度是位移随时间的二阶导数,方程 1可以重写为:
m (d2y/dt2) = -k y。(方程 2)
此二阶微分方程的解决方案是众所周知的:
y(t) = (ωt + φ),罪 (方程 3)
其中,A 是振幅,ω = (k/m)1/2和相角φ取决于系统的初始条件。中的方程 3形式的方程描述什么叫做简谐运动。周期 T,频率f,并且不断 ω 被相关的:
Ω = 2 πf = 2 π/t (方程 4)。
因此,通过给出周期 T:
T = 2 π (m/k)1/2。(方程 5)
请注意,T 不取决于振荡的振幅 A。因此,如果重量吊吊垂直的弹簧,振荡的产生时期会附加重量的平方根成正比。
拉伸弹簧所需工作距离 y 是 W = <F> y,在那里 <F> 是伸展的字符串所需的平均力。由于F是线性的y,平均是只是武力处于平衡状态 (= 0) 和y力:
<F> = ½ [0 + ky]。(方程 6)
做的工作,因此弹性势能,PE,可以写成:
PE = ½ k y2。(方程 7)
势能的春天将在这个实验室中测量。
Procedure
1.测量的弹簧常数和弹簧的势能和确认的关系质量和振荡周期 t。
- 获取与已知的弹簧常数,立场要附加到春天,至少 5 权重的不同人群,可以附加到春天,一根米尺和秒表的春天。
- 安全立场到了坚实的基础和附上春天的立场。确保有足够的空间,下面为它没有击中的表或地面伸展弹簧。
- 对于每个群众,计算由地球的引力施加在弹簧上的力 (F =毫克)。从开始的最大规模的重量。在表 1中记录这些值。
- 衡量如何高出地面的表的春天是在其未拉伸的位置中。
- 附加到春天的最巨大的重量和测量位移 Δy1 (见图 1)。在表 1中记录此位移。
- 附加的重量,略有提高重前释放它。观察振荡运动。测量周期 T 用秒表。更准确的测量,记录的多周期时间和划分当时所观察到的期数。做这个多次和记录测量周期 T表 1中的平均时间。
- 重复步骤 1.5-1.6,所有的群众,在订单的质量增加。
- 计算为每个不同的群众弹簧势能和记录在表 1中。
- 情节的力F作为位移 Δy的函数。根据方程 1,这应该是线性的。适合边坡线。该边坡将对应于弹簧常数 k.春天的已知值的测量值比较。
- 使用已知的弹簧常数和方程 5,计算振荡周期 T 应为每个群众;报告他们在表 1中。它们比作测量用秒表在步 1.6 T。
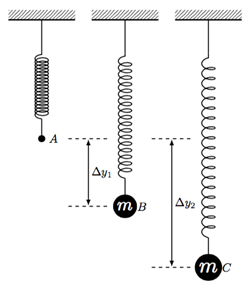
图 1: 霸气振荡,
Results
代表的实验,结果与弹簧常数k = 10m N,表 1所示。F与位移 Δy的情节是下面绘制在图 2中。线性函数拟合一条线,和直线斜率等于弹簧常数,在误差范围内。线性度的结果表明,胡克定律 (方程 1)。
检查表 1以查看如何振荡周期 T 附加到春天的质量有关。越重附加到春天,期限越长的质量会,因为它是大众 (方程 5) 的平方根成正比。另外,请注意,当较大的质量附加到春末,春天将进一步延伸。系统的潜在能量较大,因为它是从平衡 (方程 7) 平方位移的函数。时间较长的一大弥撒有道理 — — 因为春天流离失所进一步平衡,它需要更长的时间去旅行,更长的距离。
表 1。结果。
| 质量 (公斤) | 重量 / F (N) | Δy (m) | PE (J) | T 测量 (s) | 计算 T (s) |
| 0.5 | 4.9 | 0.49 | 2.4 | 1.3 | 1.4 |
| 0.75 | 7.4 | 0.74 | 5.4 | 1.6 | 1.7 |
| 1 | 9.8 | 0.98 | 9.6 | 1.9 | 1.9 |
| 1.5 | 14.7 | 1.5 | 21.6 | 2.5 | 2.4 |
| 2 | 19.6 | 2 | 38.4 | 2.9 | 2.8 |
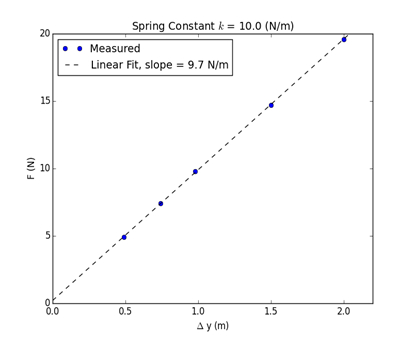
图 2: 情节的作用力 (N) 与位移。
Application and Summary
弹簧的使用是在我们的日常生活中无处不在。现代汽车的悬架是由正常阻尼的弹簧。这就需要知识的弹簧常数。凯迪拉克兜风顺畅,使用弹簧与较低的弹簧常数,和骑的是"mushier"。高性能的汽车使用弹簧与更高的弹簧常数更好的处理。跳水板也是用不同的弹簧常数,取决于"反弹"多少渴望当跳水板弹簧。岩石攀岩绳也是略有弹性,因此如果一名登山者攀爬时,绳子将不仅救她撞到地上,但它也会抑制秋天与它的弹性。越小的登山绳弹簧常数,越接近它类似于蹦极。
在此研究中,测量位移的弹簧产生的力的不同程度的应用。胡克定律的正确性通过绘制结构的位移作为函数的后悬挂弹簧施加的力。振荡运动也观察到,随着时间的平方根成正比的附加到春天的质量。
跳至...
此集合中的视频:

Now Playing
胡克的法律和简谐运动
Physics I
61.6K Views

牛顿的运动定律
Physics I
76.9K Views

力和加速度
Physics I
79.6K Views

在多个方向向量
Physics I
182.7K Views

运动学和抛体运动
Physics I
73.1K Views

牛顿的万有引力定律
Physics I
192.7K Views

动量守恒
Physics I
43.6K Views

摩擦
Physics I
53.1K Views

平衡和自由体图
Physics I
37.6K Views

扭矩
Physics I
26.2K Views

转动惯量
Physics I
43.8K Views

角动量
Physics I
36.6K Views

能源和工作
Physics I
50.3K Views

焓
Physics I
60.6K Views

熵
Physics I
17.8K Views
版权所属 © 2025 MyJoVE 公司版权所有,本公司不涉及任何医疗业务和医疗服务。