Loi de Hooke et mouvement harmonique simple

Source : Ketron Mitchell-Wynne, PhD, Antonella Cooray, Ph.d., département de physique & astronomie, école de Sciences physique, University of California, Irvine, CA

Énergie potentielle est un concept important en physique. Énergie potentielle est l’énergie associée aux forces qui dépendent de la position d’un objet par rapport à son environnement. Gravitationnel énergie potentielle, qui est discuté dans une autre vidéo, est l’énergie associée qui est directement proportionnelle à la hauteur d’un objet au-dessus du sol. De même, il est possible de définir énergie potentielle de printemps, qui est directement proportionnelle au déplacement d’un ressort de son état de relaxation. Un ressort étiré ou comprimé a énergie potentielle, comme il a la possibilité de faire un travail sur un objet. La « capacité d’effectuer un travail » est souvent citée comme la définition fondamentale de l’énergie.

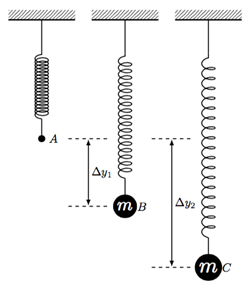
Cette vidéo fera la démonstration de l’énergie potentielle stockée en ressorts. Il vérifiera également l’équation restauration de force des ressorts, ou loi de Hooke. La constante du ressort est différente pour les ressorts des élasticités différentes. Loi de Hooke sera vérifiée et la constante de ressort mesurée en joignant les différents poids à un ressort de suspension et de mesurer les déplacements qui en résultent.

Tenant un ressort soit dans sa position comprimée ou étirée exige que quelqu'un ou quelque chose exerce une force sur le ressort. Cette force est directement proportionnelle au déplacement, Δy, du printemps. À son tour, le printemps va exercer une égale et opposée forcer :

F = -k Δy, (équation 1)

où k est appelé la « constante de raideur du ressort. » On parle souvent d’une « force de rappel » parce que le ressort exerce une force dans la direction opposée au déplacement, indiquée par le signe négatif. Équation 1 est appelée Loi de Hooke.

Mouvement harmonique simple se produit chaque fois qu’il y a une force de rappel qui est proportionnelle au déplacement de l’équilibre, comme c’est dans la Loi de Hooke. De la seconde loi de Newton, F = maet reconnaissant que l’accélération a est la dérivée seconde de déplacement en fonction du temps, 1 équation peut être réécrite sous la forme :

m (d²y/dt²) = y -k. (Équation 2)

La solution à ce différentiel du second ordre est bien connue pour être :

y (t) = A sin (ωt + φ), (équation 3)

où : A représente l’amplitude d’oscillation, ω = (k/m)^1/2et la phase angle φ varie selon les conditions initiales du système. Équations sous la forme de l’équation 3 décrivent ce qu’on appelle un mouvement harmonique simple. La période T, la fréquence fet la constante ω sont liées par :

Ω = 2πf = 2π/T. (équation 4)

Ainsi, la période T est donnée par :

T = 2π (m/n)^1/2. (Équation 5)

Notez que T ne dépend pas de l’amplitude A d’oscillation. Par conséquent, si un poids est suspendu à un ressort de suspension à la verticale, la période résultante d’oscillation serait proportionnelle à la racine carrée du poids attaché.

Le travail nécessaire pour tendre le ressort une distance y est W = <F> y, où <F> est la force moyenne nécessaire pour tendre la chaîne. Puisque F est linéaire en y, la moyenne est juste la force à l’équilibre (= 0) et la force à y:

<F> = ½ [0 + ky]. (Équation 6)

Le travail effectué et donc l’énergie de potentielle élastique, PE, peuvent être écrite comme :

PE = ½ k y². (Équation 7)

On mesurera l’énergie potentielle d’un ressort dans ce laboratoire.

1. mesurer la constante du ressort et l’énergie potentielle d’un ressort et confirmer la relation entre la masse et oscillatoire période T.

1. Obtenir un ressort avec une constante connue de printemps, un support pour fixer le ressort à, au moins 5 caractères de masses différentes qui peuvent être attachés au printemps, un bâton de compteur et un chronomètre.
2. Fixer le support à une fondation solide et attachez le ressort sur le support. Assurez-vous qu’il y a suffisamment d’espace sous le ressort pour qu’il puisse s’étirer sans heurter la table ou au sol.
3. Pour chacune des masses, calculer la force exercée sur le ressort de la force de gravitation de la terre (F = mg). Commencez par le poids moins massif. Enregistrez ces valeurs dans le tableau 1.
4. Mesurer la hauteur au-dessus de la surface de la table au printemps est tandis que, dans sa position non tendue.
5. Fixez la moins massif au printemps et mesurer la Δy1 de déplacement (voir la Figure 1). Enregistrer ce déplacement dans le tableau 1.
6. Avec le poids attaché, soulever légèrement le poids avant de le relâcher. Observer le mouvement oscillatoire. Mesurer la période T avec un chronomètre. Pour une mesure plus précise, enregistrer le temps pour plusieurs périodes et diviser ce temps par le nombre de périodes observées. Faire ce plusieurs fois et d’enregistrer le temps moyen mesuré pour la période T dans le tableau 1.
7. Répétez les étapes 1.5-1.6 pour l’ensemble des masses, par ordre croissant de masse.
8. Calculer l’énergie potentielle du ressort pour chacune des différentes masses et de les enregistrer dans le tableau 1.
9. Tracer la force F en fonction du déplacement Δy. Selon l’équation 1, ce doit être linéaire. Monter une pente de la ligne. Cette pente correspondra à la printemps constante k. comparer la valeur mesurée à la valeur connue du ressort.
10. À l’aide de la constante du ressort connue et l’équation 5, calculer ce que la période T d’oscillation devrait être pour chacun des masses ; Signalez-les au tableau 1. Comparez-les aux T qui a été mesurée avec un chronomètre à l’étape 1.6.

Figure 1 : Srping oscillation,

Des résultats représentatifs de l’expérience, menée avec un ressort de constante k = 10 N/m, sont présentées au tableau 1. L’intrigue de F par rapport à Δ de déplacementy est tracée ci-dessous à la Figure 2. La fonction linéaire est dotée d’une ligne, et la pente de la courbe est égale à la constante de ressort, avec une marge d’erreur. La linéarité du résultat montre la validité de la Loi de Hooke (équation 1).

Inspectez le tableau 1 pour voir comment la période T d’oscillation est liée à la masse qui est attachée au printemps. Plus la masse attachée au printemps, plus la période sera, comme elle est proportionnelle à la racine carrée de la masse (équation 5). Notez également que lorsqu’une masse plus importante est attachée à la fin du printemps, le printemps sera tendu plus loin. L’énergie potentielle du système est plus grande, car c’est une fonction du déplacement de l’équilibre (équation 7) au carré. Il est logique que le délai est plus long pour une masse plus importante — parce que le printemps soit déplacé plus loin de l’équilibre, il faudra plus de temps pour parcourir cette distance plue.
Le tableau 1. Résultats.

Masse (kg)	Poids / F (N)	Δy (m)	PE (J)	T mesurée (s)	T calculé (s)
0,5	4.9	0,49	2.4	1.3	1.4
0,75	7.4	0,74	5.4	1.6	1.7
1	9.8	0,98	9.6	1,9	1,9
1.5	14,7	1.5	21,6	2.5	2.4
2	19.6	2	38,4	2.9	2.8

Figure 2 : Représentation graphique de force appliquée (N) par rapport aux déplacements.

L’utilisation des ressorts est omniprésente dans notre vie quotidienne. La suspension des voitures modernes est issue de ressorts qui sont bien amorties. Cela nécessite la connaissance des constantes printemps. Pour des promenades plus lisses de Cadillac, ressorts avec une constante de ressort inférieur sont utilisés, et le trajet est « mushier ». Les voitures haute performance utilisent des ressorts avec une constante de ressort supérieure pour une meilleure manipulation. Tremplins sont aussi faites avec des ressorts des constantes différentes printemps, dépendant de « rebondir » combien est souhaitée lors d’une plongée hors du plateau. Cordes d’escalade sont également légèrement élastiques, donc si un alpiniste tombe alors qu’il montait, la corde va non seulement sauver de heurter le sol, mais il freinera aussi la chute avec son élasticité. Plus la constante du ressort d’une corde d’escalade, plus il ressemble beaucoup à saut.

Dans cette étude, a été mesuré le déplacement d’un ressort résultant de l’application des forces d’amplitudes variables. La validité de la Loi de Hooke a été vérifiée en traçant les déplacements qui en résultent en fonction de la force exercée sur le ressort de suspension. Mouvement oscillatoire observa aussi, avec des périodes proportionnelles à la racine carrée de la masse attaché au printemps.