Generation und kohärente Steuerung der gepulsten Quantum Frequenzkämmen

Zusammenfassung

Ein Protokoll ist für die praktische Erzeugung und kohärente Manipulation von hochdimensionalen Frequenz-bin verstrickt Photon Staaten mit integrierten Mikro-Hohlräumen und standard Telekommunikation Komponenten bzw. vorgestellt.

Zusammenfassung

Wir präsentieren eine Methode zur Erzeugung und kohärente Manipulation von Frequenzkämmen gepulster Quanten. Bis jetzt sind Methoden zur Vorbereitung hochdimensionalen Staaten auf Chip auf praktische Weise schwer aufgrund der zunehmenden Komplexität der Quanten-Schaltung zur Vorbereitung und Verarbeitung solcher Staaten geblieben. Hier beschreiben wir wie hochdimensionalen, Frequenz-bin verstrickt, zwei-Photonen-Staaten können durch erzeugt werden mit einer stabilen, Generation Rate eine verschachtelte Hohlraum, aktiv modengekoppelten Anregung von nicht-linearen Mikro-Kavitäten. Diese Technik wird verwendet, um gepulste Quantum Frequenzkämmen produzieren. Darüber hinaus präsentieren wir wie die Quantenzustände kohärent sein kann mit standard Telekommunikation Komponenten wie programmierbare Filter und elektrooptische Modulatoren manipuliert. Insbesondere zeigen wir im Detail wie Zustand Charakterisierung Messungen wie Dichte Matrix Rekonstruktion, koinzidenzerkennung und einzelnes Photon Spektrum Bestimmung zu erreichen. Die vorgestellten Methoden bilden eine zugängliche, rekonfigurierbare und skalierbare Grundlage für komplexe hochdimensionalen Staat Vorbereitung und Manipulation Protokolle im Frequenzbereich.

Einleitung

Die Kontrolle der Quantenphänomene eröffnet die Möglichkeit für neue Anwendungen in so unterschiedlichen Bereichen wie sichere Quanten Kommunikation¹, leistungsstarke Quantum Informationsverarbeitung²und Quantum sensing³. Während eine Vielzahl von physischen Plattformen sind für die Erkenntnisse der Quantenphysik Technologien⁴aktiv erforscht, sind optische Quantenzustände wichtige Kandidaten wie sie mal lange Kohärenz und Stabilität von Außenlärm, ausgezeichnete aufweisen können Übertragungseigenschaften sowie Kompatibilität mit bestehenden Telekommunikations- und Silizium-Chip (CMOS)-Technologien.

In Richtung voll erkannte das Potenzial von Photonen für Quantentechnologien, kann durch den Einsatz mehrerer verwickelten Parteien und/oder High-Dimensionalität Zustand Komplexität und Informationsgehalt erhöht werden. Allerdings fehlt die auf Chip-Generation solcher optischen Staaten Praktikabilität Setups sind kompliziert, nicht perfekt skalierbare bzw. hochspezialisierten Komponenten verwenden. Insbesondere hochdimensionalen Pfad-Verstrickung erfordert zusammenhängend aufgeregt identisch Quellen und aufwendige Schaltungen der Strahlteiler⁵ (wo ist die Staat Dimensionalität), während Zeit-Verstrickung komplexe braucht Multi-Arm Interferometer⁶. Bemerkenswert ist, der Frequenzbereich eignet sich gut für die skalierbare Erzeugung und Steuerung komplexer Zustände, dargestellt durch seine jüngsten Ausbeutung in Quantum Frequenz Kämme (QFC)^7,8 mit einer Kombination aus integrierten Optik und Telekommunikations-Infrastrukturen⁹, und bietet einen viel versprechenden Rahmen für zukünftige Quantum Information Technologies.

Auf dem Chip QFCs entstehen integrierte Micro-Hohlräume nichtlineare optische Effekte bei. Mit solchen nichtlinearen Mikro-Resonator, sind zwei verschränkte Photonen (angegeben als Signal und Müßiggänger) produziert durch spontane vier-Wellen-mischen, über die Vernichtung der beiden Erregung Photonen - mit dem daraus resultierenden Paar in einer Überlagerung der Kavität erzeugt gleichmäßig verteilt Resonanzfrequenz Modi (Abbildung 1). Wenn es Kohärenz zwischen den einzelnen Frequenz-Modi, ist ein Frequenz-bin verstrickt Staat gegründeten¹⁰, die oft als eine modengekoppelten zwei Photon staatliche¹¹bezeichnet wird. Dieser Zustand Wellenfunktion kann durch beschrieben werden:

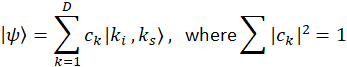
Hier, 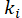und 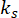sind die Monomode-Frequenz Müßiggänger und Komponenten, bzw. signal und 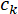ist die Wahrscheinlichkeit Amplitude für die -ten Signal-Faulenzer-Modus Paar.

Früheren Demonstrationen auf dem Chip QFCs markieren Sie ihre Vielseitigkeit als tragfähige Quantum Informationsplattformen und umfassen Waben korrelierte Photonen¹², Kreuz-polarisierte Photonen¹³, verschränkte Photonen^{14,15 , 16}, Multi-Photonen erklärt¹⁵, und Frequenz-bin verstrickt Staaten^9,17. Hier bieten wir einen detaillierten Überblick über die QFC-Plattform und ein Protokoll für hochdimensionale Frequenz-bin verstrickt, optische State-Erzeugung und Kontrolle.

Künftigen Anwendungen, insbesondere solche mit High-Speed-Elektronik (für die zeitgerechte Informationsverarbeitung), verbunden sein Verlangen die Hochrate-Generation von hochreinen Photon Staaten in einem kompakten und stabilen Aufbau. Wir verwenden eine aktiv-Modus gesperrt, geschachtelte Hohlraum-Schema, um QFCs in der Telekommunikation S, C und L Frequenzbänder zu produzieren. Ein Mikro-Ring ist in einem größeren gepulste Laser Hohlraum, mit optische Verstärkung (bereitgestellt von einem Erbium-dotierte Faser-Verstärker, EDFA) gefiltert, um die Mikro-Ring Erregung Bandbreite¹⁸übereinstimmen integriert. Modus-Verriegelung wird aktiv über Elektro-optische Modulation der Kavität Verluste¹⁹realisiert. Ein Isolator sorgt dafür, dass Puls Ausbreitung eine einzige Richtung folgt. Die daraus resultierende Impulsfolge hat sehr niedrige Root-Mean-Square (RMS) Lärm und Ausstellungen einstellbaren Wiederholraten und Puls Befugnisse. Hohe Isolation Notch-Filter trennt die emittierten QFC Photonen aus dem Bereich der Erregung. Diese einzelnen Photonen werden dann durch Fasern für Kontrolle und Nachweis geführt.

Unsere Regelung ist ein Schritt in Richtung einer hohen Generation-Rate, kompakte QFC Quelle, da alle verwendete Komponenten möglicherweise auf einem photonischen Chip integriert werden können. Darüber hinaus ist gepulste Anregung besonders gut geeignet für Quanten-Anwendungen. Erstens erzeugt mit Blick auf ein paar Micro-Cavity Resonanzen symmetrisch zu der Anregung, es zwei-Photonen-Staaten, wo jedes Photon ist gekennzeichnet durch eine Einzel-Frequenz Modus – Zentrale für lineare optische Quantencomputer²⁰. Darüber hinaus können Multi-Photonen-Staaten durch höhere Macht Erregung Regimes und Auswählen von mehreren Signal-Faulenzer Paare¹⁵erzeugt werden. Zweitens wie Photonen in bekannten Zeitfenster entsprechend der gepulsten Anregung emittiert werden, Nachbearbeitung und Anspritzung realisierbar um Zustand Erkennung zu verbessern. Vielleicht unterstützt vor allem unsere hohen Raten von Photon Staaten mit harmonischen Modus-Verriegelung, ohne Verringerung der Zufall zu zufälligen Verhältnis (Auto) – das könnte den Weg für High-Speed-, multi-Channel Quanteninformation Technologien.

Um die Auswirkungen und die Machbarkeit der Frequenz-Domäne zu demonstrieren, muss die Kontrolle der QFC Staaten auf gezielte Weise, hocheffiziente Transformationen und Staat Kohärenz zu gewährleisten durchgeführt werden. Um diesen Anforderungen gerecht zu werden, verwenden wir kaskadierten programmierbare Filter und Phase Modulatoren – bewährte Komponenten in der Telekommunikationsbranche. Programmierbare Filter lässt sich eine beliebige spektralen Amplitude und Phase Maske auf die einzelnen Photonen mit einer Auflösung ausreichend, um jede Frequenzmodus individuell anzusprechen zu verhängen; und Phase elektrooptische Modulatoren angetrieben durch Radiofrequenz (RF) Signalgeneratoren ermöglichen das Mischen von Frequenz Komponenten²¹.

Der wichtigste Aspekt dieser Regelung ist, dass sie auf alle Quantum-Modi der Photonen gleichzeitig in einem einzigen räumlichen Modus, über einzelne Bedienelemente arbeitet. Erhöhung der Quantenzustand Dimensionalität führt nicht zu einer Erhöhung der Setup-Komplexität, im Gegensatz zu Weg-Zeit bin Verschränkung Systeme. Darüber hinaus sind alle Komponenten extern rekonfigurierbare (d. h. die Vorgänge verändert werden können, ohne eine Änderung das Setup) und bestehende Telekommunikationsinfrastruktur zu verwenden. So können bestehende und kommende Entwicklungen auf dem Gebiet der ultraschnelle optische Verarbeitung direkt an die skalierbare Steuerung von Quantenzuständen in Zukunft übertragen werden.

Zusammenfassend lässt sich sagen die Ausbeutung der Frequenzbereich von QFCs unterstützt die Hochrate-Generation von komplexen Quantenzustände und deren Kontrolle, und eignet sich somit für die Nutzung komplexer Zustände auf praktische und skalierbare Quantentechnologien.

Protokoll

1. Generation des hochdimensionalen Frequenz-Kastens verstrickt Staaten über gepulste Anregung

1. Im Anschluss an das Schema in Abbildung 2 (Erzeugungsstufe) beschrieben verbinden Sie jede Komponente mit Lichtleitfasern Polarisation-Pflege (für verbesserte Umweltstabilität).
2. Verbinden Sie ein Netzteil mit der Amplitude der elektrooptischen Modulator und wenden Sie einen DC-Spannung-Offset tuning des Offset-Werts, bis die optische Leistung durch es übertragen etwa halbiert wird (gemessen mit einem optische Leistungsmesser), zB., so dass eine Spitze Getriebe-Wert von 2 mW wird halbiert, bis 1 mW.
3. Messen Sie die Länge der ungefähre externe Hohlraum. Berechnen Sie den externen Hohlraum Modus Abstand unter Zugrundelegung der Beziehung,
   
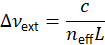
   wo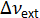 ist der externe Hohlraum Modus Abstand, c ist die Lichtgeschwindigkeit im Vakuum, 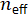ist der effektive Index des Mediums Hohlraum und L ist die Länge der äußeren Hohlraum. Zum Beispiel wäre die ungefähre Hohlraum Modus Abstand für einen 20 m-Hohlraum bestehend aus Glasfaser mit einer effektiven Brechungsindex 1,46, 10,2 MHz.
4. Schalten Sie die EDFA lasing einzuleiten.
5. Legen Sie die schnelle Fotodiode in das Setup auf den Hohlraum-Koppler oder anderen ringports. Verbinden Sie Fotodiode Signal auf einem Oszilloskop die Erregung Feldstärke in den Zeitbereich zu beobachten.
6. Die Oszilloskop-Zeitauflösung soll < 100 Ps (durch die horizontale Skalierung Knopf) um die ns-Skala Impulse zu lösen. Bei diesem Schritt wird ohne den Modulator aktiviert, die Ausgabe auf dem Oszilloskop instabil Pulsbetrieb mit einer niedrigen Qualität, hohen Geräuschpegel Impulsfolge zeigen.
7. Verbinden Sie einen Funktionsgenerator mit der Amplitude der elektrooptischen Modulator. Stellen Sie die Frequenz des Generators Funktionsausgang die (ungefähre) externe Hohlraum Modus Abstand oberhalb (oder einer harmonischen). Dieses Signal führt die Modus-Verriegelung. Wählen Sie entweder ein Puls (rechteckig) Wellenform oder Sinuswelle für Amplitudenmodulation. Schalten Sie den Funktionsgenerator.
8. Stimmen Sie die RF-Funktion Generator Frequenz und DC offset zur Optimierung und Stabilisierung der Impulsform Zug auf dem Oszilloskop. Signal wird verwendet, wenn eine gepulste fahren, die Einschaltdauer zu optimieren.
9. Manuell anpassen den EDFA-Gewinn zu verringern (oder erhöhen) Impulsintensität gegen das Regime, wo die Eigenschaften der erzeugten Photonen sind, wie gewünscht durch den Benutzer (Auto ist hier eine nützliche Metrik - siehe unten für Details auf die Messung). Vergleichen Sie hierzu die jeweiligen Zufall Histogramme erzeugt durch die visuelle Schnittstelle, die mit der Timing-Elektronik kommt.
10. Füttern Sie Timing Elektronik Sync Kanal mit dem Zug Pulssignal (entdeckt von der Photodiode) oder das HF-Modus-Verriegelung Signal, Einzelphotonen-Detektoren mit der Photon-paar-Generation zu synchronisieren.
11. Um die Generation der QFCs zu erhöhen, fahren die Modus-Verriegelung-Modulator bei höheren harmonischen von den externen Hohlraum Frequenzabstand während gleichzeitig Vermehrung des EDFA-Gewinns um die gleiche Leistung pro Puls zu gewährleisten – dadurch wird das Photon Auto beim koppeln steigern die paar Produktionsrate (Abbildung 3). Hierzu erhöhen Sie die Funktion Generator Ausgangsfrequenz und EDFA Gewinn bzw..

2. Beherrschung der hochdimensionalen Frequenz-bin verstrickt Staaten

1. Im Anschluss an das Schema in Abbildung 2 (regelstufe) beschrieben Verbindung aller Elemente mit Polarisation Aufrechterhaltung Fasern. Verbinden Sie der Notch-Filter in der Generation-Regelung ab, in Serie die erste programmierbare Filter, Phase Modulator und zweite programmierbare Filter. Schließlich verbinden Sie die Einzelphotonen-Detektoren für Zwecke der Messung.
2. Programmierbare Filter Betrieb
   Hinweis: Abhängig von der spezifischen Anwendung/Messung durchgeführt wird, die Regelparameter des QFC variiert und die Phase und Amplitude Masken angewendet, die Frequenz-Modi müssen entsprechend ermittelt werden. Die Amplitude Maske lässt sich mildern oder blockieren bestimmte Frequenz-Modi und die Phase-Maske kann eine willkürliche Phasenverschiebung auf jeden Modus vermitteln.
   1. Die notwendigen Masken für die gewünschte Anwendung/Messung zu bestimmen.
   2. Legen Sie über die programmierbare Filter visuelle Schnittstelle²²die Amplitude der gewünschten Frequenz Modus Kanäle und dämpfen Sie alle anderen.
   3. Ebenso gelten Sie die Phase-Maske (die Phase auf die unerwünschte Kanäle angewendet ist unwichtig, da sie vollständig gedämpft sind). Steuern Sie die programmierbare Filter mit einer visuellen Schnittstelle, wo die gewünschten Frequenzen ausgewählt werden.
3. Phasenmodulation Betrieb
   1. Phasenmodulation, angetrieben durch ein periodisches Signal mit einzelnen spektralen Komponenten in Seitenbänder durch die Frequenz des Signalgenerators die Phase Modulator treibt gleichmäßig aufgeteilt. Hiermit können Sie um mehrere verschiedene Quanten Frequenz-Modi, mit räumlichen Strahlteiler im Pfad-Verstrickung Regelungen analog zu mischen. Elektrooptische Phasenmodulation gilt in der Quanten-Regime eine Quantum Streuung Betrieb²³.
   2. Bestimmen die Ziel-Frequenz-Modi (abhängig von und die Messung/Verarbeitung durchgeführt wird) und die Spannung-Muster (Frequenz und Amplitude für eine Sinus-Generator) berechnen, um die gewünschte Optimierung 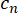Werte (siehe unten für einige Details hierzu).
   3. Verbinden Sie den Signalgenerator mit der HF-Verstärker mit verlustarmen Kabeln (z. B. SMC Kabel). Verbinden Sie den HF-Verstärker-Ausgang mit der Phase Modulator, auch mit ausreichenden HF-Kabel. Sobald alle RF Enden verbunden sind und ordnungsgemäß beendet, die HF-Verstärker-bias.
   4. Sicherzustellen, dass die HF-Verstärker ausreichende Ausgangsleistung hat, die elektro-optischen Phase Modulator mit ausreichend Spannung die gewünschte Mischung erfüllen zu fahren – handelt es sich in der Größenordnung von mehreren 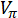(die Halbwellen-Spannung des Modulators Phase). Stellen Sie außerdem sicher, dass das HF-Kabel und Steckverbinder für die Bandbreite und Frequenz Auswahl an die ansteuersignalerzeugungseinrichtung ausreichend sind.
   5. Eine Frequenz, die die gewünschte Modi mit der erstellten Seitenbänder überlappen den RF Signalgenerator (die Phase Modulator treibt) festgesetzt (zB., 33 GHz).
   6. Schalten Sie den Signalgenerator, der Frequenz-Modi zu mischen.
   7. Um sicherzustellen, dass die richtige Modulation angewendet wird, senden Sie einen Dauerstrich-Laser durch die Phase Modulator und überprüfen Sie, ob das ausgangsspektrum die vorgesehene Modulation mit Hilfe eines optischen Spektrumanalysator entspricht (die Modulation Parameter können weitere werden optimiert, siehe Anmerkungen).
      Hinweis: Optimiert die Durchmischung des Frequenz-Modi (Bestimmung der optimalen Funktion Frequenz und Amplitude) ist stark abhängig von der gewünschten Misch-Schema, experimentieren durchgeführt wird und staatliche Dimensionalität . Wenn möglich, sollten mischen Systeme Modi in der Nähe der ersten Frequenzmodus (bei Low-Ganzzahl Seitenbänder) mischen, um die mischenden Leistungsfähigkeit erhöhen. Zum Beispiel, wenn 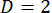, die Vermischung wird empfohlen, auf halbem Weg zwischen den zwei Frequenz-Modi auftreten (so die Phasenmodulation sollten Gefahren werden auf eine Frequenz, die eine Ganzzahl mehrere gleich die Hälfte hat die Quanten-Modus Frequenz Abstand oder frei Spektralbereich (FSR)). Jedoch für 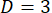, mischen wird empfohlen, in die Center-Frequenz-Modus (Phase Modulation sollte bei einer Frequenz mit Integer mehrere gleich zu der FSR Gefahren werden) auftreten. Z. B. mit 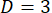und Mikro-Hohlraum 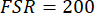GHz, die Phasenmodulation fahren Signal auf 33,33 GHz festgelegt ist, dass die 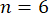Seitenband überschneidet sich mit den benachbarten Frequenz-Modi - wobei auch ausreichenden Intensität in der Mitte Frequenzmodus. Dadurch wird die Überlappung der Seitenbänder benachbarten Modi 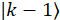, 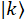und 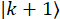auf die Center-Frequenz-Modus 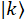. Abbildung 4a visualisiert ein Beispiel für die Modulation und Seitenband-Koeffizienten. Jede Frequenzmodus erfährt die gleiche Phase Modulation und schafft die gleiche Seitenband-Verteilung, aber zentriert über der ursprünglichen Frequenzmodus (Abb. 4a). Für eine einzelne Frequenz-Modus die Seitenband Amplituden als die Koeffizienten der Fourier-Reihen²⁴berechnet werden,
      
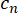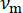      wo wird die Amplitude übertragen die -ten Seitenband, ist die Frequenz, die der Phase Modulator, angetrieben wird 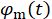ist die Phasenmodulation Muster (periodische mit Frequenz 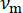), und 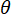ist die Argument der Funktion periodische Modulation (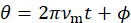). Für eine sinusförmige ansteuersignalerzeugungseinrichtung 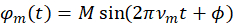, Seitenband Amplituden werden beschrieben durch die Jacobi-Wut-Expansion
      
      
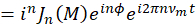
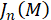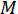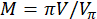      wo ist die -ter Ordnung Bessel Funktion von der ersten Art bewertet und ist die maximale Phasenverschiebung (wo 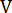ist die Spannungsamplitude des einstufiges treibende Signals).

(3) die Verarbeitung von hochdimensionalen Frequenz-bin verstrickt Staaten

1. Einzelphotonen-Spektrum
   1. Legen Sie einen einzelnes Photon-Detektor nach der Filterung des Feldes Anregung aus der QFC am Ausgang eine programmierbare Filter.
   2. Fegen Sie über die programmierbare Filter-Computer-Software über die voll programmierbare Filter-Bandbreite mit Hilfe einer schmalen Bandpass Filter Amplitude Maske, Photon Zählraten als Funktion der Frequenz zu messen. Zum Beispiel wenn eine visuelle Schnittstelle/Kontrolle Skript in MATLAB dient (das mit der programmierbaren Filtersteuerung und Timing Elektronik verbunden ist), geben Sie die gewünschte Bandbreite Filterwerte und Schritt Nummer und klicken Sie auf "Ausführen". Sicherstellen Sie, dass ausreichend Integrationszeit zu richtigen Photon zählt.
   3. Um das Spektrum aus diesen Daten zu rekonstruieren, Grundstück (z. B. mit einem Matlab-Skript) die Photon Zählraten gegen die entsprechende Wellenlänge (Bandpass filter Mitte) wo sie erworben wurden.
2. Zufall-Messung
   1. Um einen Zufall-Messung durchzuführen, teilen Sie und leiten Sie das Signal und die Spannrolle Photonen Einzelphotonen-Detektoren zu trennen. Wenn die programmierbare Filter mehrere Anschlüsse verfügt, können sie die Trennung durchführen. Andernfalls legen Sie eine Dichte Wellenlänge Division multiplexer (DWDM) vor der Einzelphotonen-Detektoren und verwenden Sie diese Option zum Weiterleiten der Photonen.
   2. Wählen Sie ein Signal und die Spannrolle Paar (z. B. die zweite resonanzlinien im Hinblick auf die Erregerfrequenz, Signal-2 und Faulenzer-2) mit der programmierbaren Filtern (über die mitgelieferte Software-Schnittstelle) und leiten Sie sie an zwei separaten Einzelphotonen-Detektoren. Zum Beispiel für die WaveManager-Software, klicken Sie auf das Untermenü "FlexTabelle", klicken Sie auf "Hinzufügen" und geben Sie die Wellenlänge und Output Port für den gewählten Kanal²².
   3. Notieren Sie die Ankunftszeit des Signals und Spannrolle Photonen mit dem Zeit-zu-Digital-Konverter. Aus diesen Messungen ist die zeitliche Verzögerung zwischen den beiden Photonen zu berechnen. Grundstück ein Histogramm (z. B. mit einem Matlab-Skript) zählt für eine Zeitverzögerung von Zufall zwischen Signal und Müßiggänger – Dies bietet eine Zufall-Messung.
      Hinweis: Die Auto-Metrik vergleicht die Anzahl der echten Zufall Grafen aus die generierte Photon-Paare mit den zufälliges Zusammentreffen Grafen aus Multi-Photonen-Prozesse und dunklen zählt.
   4. Aus der oben berechneten Bewertung, notieren Sie die Anzahl der Grafen in der Mitte-Spitze (Zufälle aus Photonen, die in der gleichen Puls, zentriert um die NULL Verzögerung produziert 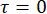) – Zufall Wert.
   5. Notieren Sie die durchschnittliche Anzahl der Grafen in jede Seite-Spitze (Zufälle von Photonen in verschiedenen Impulsen erzeugt wo ist ein Vielfaches der Puls trainieren, dh., das Gegenteil von der Pulswiederholrate), zufälligen Wert.
      Hinweis: Das Auto ist einfach das Verhältnis dieser beiden Werte (Zufall Wert/zufälligen Wert).
3. Dichte Matrix Wiederaufbau
   Hinweis: Für Dichte Matrix Wiederaufbau richtet sich nach mehreren Parametern von den Quantenzustand: die Dimensionalität der Photonen, die Anzahl der Photonen, und welche Betriebsarten gemessen werden. Die Anzahl der rohen Messungen erforderlich ist gleich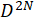, woist die Dimensionalität und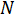ist die Anzahl der Photonen. So zum Beispiel, ein zwei-Photonen-Paar mit einem Dimensionalität der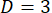81 Messungen benötigen. Dieses Protokoll wird einen Überblick über die allgemeine Vorgehensweise zur Dichte Matrix Wiederaufbau, mit Beispielen für ein paar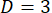Frequenz-Modus Photonen.
   1. Bestimmen Sie eine Reihe von Basisvektoren für den gewünschten Zustand und ein Satz von Projektion Vektoren (siehe unten für Details wie diese entsprechend wählen).
   2. Verwenden Sie mit einem Zufall Messung entweder eine programmierbare Filter oder ein DWDM-Weg-Signal und Spannrolle Photonen Einzelphotonen-Detektoren zu trennen.
   3. Wählen Sie über die programmierbare Filter-Software-Steuerung die gewünschte Frequenz-Modi und vermindern Sie alle anderen zu. Legen Sie die Phase Maskenwerte ein Zufall-Messung zu jeder Projektion Wavevector individuell zu realisieren. Es ist wichtig, um die gleichen Integrationszeit zwischen verschiedenen Projektion Zufall zählt zu ermöglichen.
   4. Mit einem benutzerdefinierten Computer-Skript, Berechnen der Dichtematrix der Photonen mit der rohen Zufall Graf Messungen von jeder Projektion Wavevector (computational Einzelheiten siehe unten).
      Hinweis: Wenn Sie Basisvektoren für die Messung der Dichte Matrix zu bestimmen, müssen sie der Zustandsraum umfassen. Für den Beispielfall sind die Basisvektoren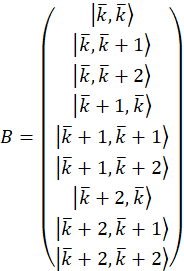
      
      Für einen Staat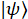 , die Dichtematrix beschreibt den Quantenzustand,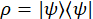
      
      Die Dichtematrix sein für jedes echte physikalische System muss eine positiv-definitive, hermitesche Matrix - aber wegen Lärm, dies nicht immer kann der Fall. In dem Beispielfall mit der gewählten Basis kann die Wavevector für den Idealzustand maximal Frequenz verstrickt als dargestellt werden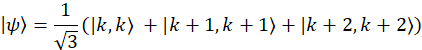
      
      und so wäre die theoretischen Dichtematrix:
      
      Projektion Messungen auf einer Reihe von Projektion Wavevectors,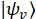 . Zufall zählt für jede Projektion werden als gegeben,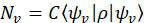
      
      wo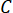 ist eine Konstante (Definition siehe unten).
   5. Wählen Sie eine orthogonale Gruppe von 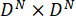, normalisiert, Matrizen, 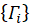, so dass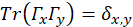
      
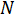      wo ist die Spur, ist die Dimension ist die Anzahl der Photonen, und 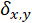ist die Kronecker-Delta-Funktion. Diese Matrizen können konstruiert werden, mit der speziellen einheitlichen SU () Generatoren (davon sind 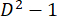), zusammen mit der Identitätsmatrix, durch alle möglichen Tensor Produkt Kombinationen²⁵. Siehe unten für die orthogonalen Matrizen der Beispielfall.
   6. Rekonstruktion der Dichtematrix, 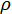, über die folgenden Beziehungen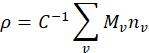
      
      
      
      
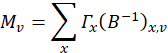
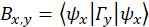
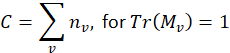
      wo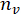 ist das Photon zählt für die -ten projektionsvektor, 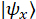sind die Projektion Vektoren (siehe nächster Schritt), wo 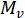und sind nach der Definition der Gleichung berechnet.
      Hinweis: Projektion Wavevectors für den Beispielfall sind,
      
      
      
      
      
      
      
      
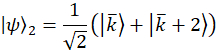
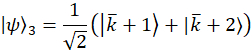
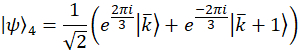
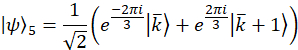
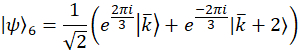
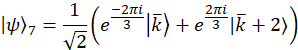
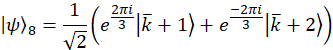
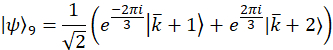
      Diese Wavevectors sind experimentell, durch Vermittlung der entsprechenden Phasenverschiebung auf jeden Modus über die programmierbare Filter realisiert. Beziehen sich auf frühere Veröffentlichung²⁵ für Diskussion über Projektion Vektoren. Die orthogonale Gruppe von Matrizen,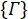 für das Beispiel sind Fall gewählt, zunächst über die SU(3) Generatoren zusammen mit der Identitätsmatrix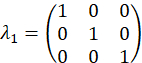
      
      
      
      
      
      
      
      
      
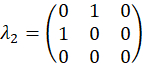
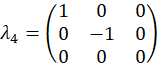
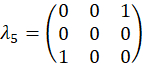
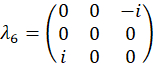
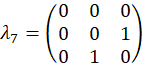
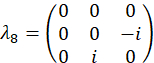
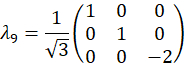
      und werden als, berechnet
      
   7. Eine tiefer gehende Diskussion über hochdimensionalen staatlichen Wiederaufbau finden Sie unter Referenz 25 ²⁵.

Ergebnisse

Die skizzierten Schema für die Erzeugung und die Kontrolle der hochdimensionalen Frequenz-bin Staaten (basierend auf der Anregung von nicht-linearen Mikro-Hohlräumen, Abbildung 1) ist in Abbildung 2dargestellt. Dieses Setup verwendet standard Telekommunikation Komponenten und ist sehr flexibel in der Photon-Produktion-Rate und die Verarbeitungen angewendet. Abbildung 3 zeigt die Charakterisierung d...

Diskussion

Die optischen Frequenzbereich über QFCs, ist vorteilhaft in Quanten-Anwendungen für eine Vielzahl von Gründen. Operationen sind global, handeln auf allen Staaten gleichzeitig, die Ergebnisse in einem Design, das nicht in der Größe oder Komplexität mit zunehmender Staat Dimensionalität skaliert wird. Dies wird verbessert, da die Komponenten on-the-Fly ohne Änderung der Einstellungen neu konfiguriert werden und sind in der Lage können, auf dem Chip integrierte durch Ausnutzung der vorhandenen und/oder Halbleiter u...

Materialien

Name	Company	Catalog Number	Comments
Superconducting Nanowire Single-Photon Detector System	Quantum Opus	Opus One
Electro-optic phase modulator	EO-Space	Low loss model
Programmable filter	Finisar	WaveShaper 4000s
Timing electronics	PicoQuant	HydraHarp 400
Micro-ring resonator			200 GHz FSR micro-ring resonator made from high refractive index glass. See Ref. 24 for platform details.
Erbium-doped fiber amplifier	Keopsys	PEFA-SP-C-PM-27-B202-FA-FA
Electro-optic amplitude modulator	Oclaro	SD40
RF tone source	Rohde & Schwarz	SMP 04
RF tone amplifier	RF-Lambda	RFLUPA27G34GA
Function generator	Tetronix	AFG 3251
Isolator	General Photonics	NISO-S-15-SS-FC/APF
Oscilloscope	Tetronix	TDS5052B
Photodiode	Finisar	XPDV 50 GHz
DWDM	OptiWorks	DWFUQUMD08BN
Power supply	Madell	CA18303D