Geração e controle coerente de pentes de frequência pulsada Quantum

Resumo

Um protocolo é apresentado para a geração prática e coerente manipulação de Estados de fóton de frequência alta dimensão-bin enredada usando integradas microcavidades e componentes de telecomunicações padrão, respectivamente.

Resumo

Nós apresentamos um método para a geração e a manipulação coerente de pentes de frequência quântica pulsado. Até agora, métodos de preparação de alta dimensão Estados em-microplaqueta de forma prática permaneceu indescritíveis devido à complexidade crescente do circuito quântica necessário para preparar e processar esses Estados. Aqui, nós esboçamos como alta dimensão, frequência-bin enredada, dois fotões Estados podem ser gerados a um ritmo estável, alta geração usando uma excitação aninhados-cavidade, ativamente modo bloqueado de uma microcavidade não-linear. Essa técnica é usada para produzir pentes de frequência quântica pulsado. Além disso, apresentamos como os estados quânticos pode ser coerentemente manipulado usando componentes padrão de telecomunicações como filtros programáveis e moduladores eletro-óptica. Em especial, mostramos em detalhes como realizar medições de caracterização do estado como reconstrução de matriz de densidade, detecção de coincidência e determinação do espectro de fóton único. Os métodos apresentados formam uma base acessível, reconfigurável e escalável para protocolos de preparação e manipulação de estado elevado-dimensionais complexas no domínio da frequência.

Introdução

O controle de fenômenos quânticos abre a possibilidade de novas aplicações em campos tão diversos como seguro quântica comunicações¹, informação quântica poderoso processamento²e quântica sensoriamento³. Enquanto uma variedade de plataformas físicas ativamente estão sendo pesquisados para as realizações de quântica tecnologias⁴, óticos estados quânticos são candidatos importantes, como eles podem apresentar vezes longo coerência e estabilidade do ruído externo, excelente Propriedades de transmissão, bem como compatibilidade com existente das telecomunicações e tecnologias de silício microplaqueta (CMOS).

No sentido de realizar plenamente o potencial de fótons para tecnologias quânticas, conteúdo de informações e a complexidade do estado pode ser aumentado com o uso de múltiplas partes emaranhadas e/ou alta-dimensionalidade. No entanto, a geração de em-microplaqueta desses Estados óptico não possui praticidade como configurações são complicadas, não perfeitamente escalável, e/ou usam componentes altamente especializados. Especificamente, requer alta dimensão caminho-emaranhamento fontes idênticas coerentemente-animado e elaborados circuitos de feixe-divisores⁵ (onde é a dimensionalidade do estado), enquanto que precisa de tempo-entrelaçamento complexo interferômetros multi braço⁶. Notavelmente, o domínio da frequência é adequado para a geração escalável e o controle dos Estados complexos, como mostrado pela sua recente exploração em quântica frequência pentes (QFC)^7,8 usando uma combinação de óptica integrada e de infra-estruturas de telecomunicações⁹e fornece um quadro promissor para as tecnologias da informação quântica futura.

QFCs em-microplaqueta são gerados usando efeitos ópticos não lineares em microcavidades integradas. Usando tal um não-linear microressonador, dois fótons emaranhados (Note-se como sinal e tensor) são produzidos por espontânea quatro ondas de mistura, através da aniquilação de dois fótons de excitação - com o par resultante gerado em uma superposição da cavidade modos de frequência ressonante uniformemente espaçados (Figura 1). Se há coerência entre os modos de frequência individual, um estado de frequência-bin enredado é formado¹⁰, que é muitas vezes referida como um estado de modo bloqueado dois fótons¹¹. Esta função de onda do estado pode ser descrita por,

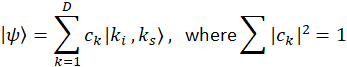
Aqui, 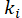e 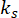são o tensor de frequência-monomodo e sinal de componentes, respectivamente, e 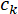é a amplitude de probabilidade para o par de modo de sinal-tensor - th.

Manifestações anteriores em-microplaqueta QFCs destacam sua versatilidade como plataformas de informação quântica viável e incluem pentes de fótons correlacionados¹², fótons polarizados Cruz¹³,^14,de fótons emaranhados^{15 , 16}, multi fóton afirma¹⁵e frequência-bin enredada Estados^9,17. Aqui, nós fornecemos uma descrição detalhada sobre a plataforma QFC e um protocolo para frequência alta dimensão-bin emaranhado controle e geração de ópticas do estado.

Aplicações futuras quântica, especialmente aqueles para ser interfaceado com eletrônica de alta velocidade (para o processamento de informações oportunas), exigem a geração de altas taxas de Estados de fótons de alta pureza em uma configuração compacta e estável. Nós usamos um esquema de cavidade ativamente modo bloqueado, aninhados para produzir QFCs dentro das Telecomunicações S, C e L bandas de frequência. Um anel de micro é incorporado uma cavidade mais ampla do laser pulsado, com ganho óptico (fornecido por um amplificador de fibra dopados com érbio, EDFA) filtrada para coincidir com a excitação de microanel de largura de banda¹⁸. Modo de bloqueio é realizado activamente através da modulação electro-óptica da cavidade perdas¹⁹. Isolador garante que a propagação do pulso segue uma única direção. O trem de pulso resultante tem ruído muito baixo raiz média quadrática (RMS) e exibe a repetência ajustáveis e poderes de pulso. Um filtro de entalhe elevado isolamento separa os fótons emitidos de QFC do campo de excitação. Estes fótons único então são guiados através de fibras de controle e de detecção.

Nosso esquema é um passo para uma alta taxa de geração, fonte QFC reduzido, como todos os componentes usados, potencialmente, podem ser integrados em um chip fotônico. Além disso, excitação pulsada é particularmente bem adaptada para aplicações de quântica. Primeiro, olhando para um par de microcavidade ressonâncias simétricas para a excitação, ele gera dois fotões Estados onde cada fóton é caracterizada por uma frequência única modalidade – central para linear óptica quântica computação²⁰. Também, fótons vários Estados podem ser gerados, movendo-se para regimes de excitação maiores poder e selecionando múltiplos pares de sinal-tensor¹⁵. Em segundo lugar, como os fótons são emitidos em janelas de tempo conhecido correspondente a excitação pulsada, pós-processamento e retenção podem ser implementados para melhorar detecção do estado. Talvez mais significativamente, o nosso esquema suporta taxas de alta geração de fótons Estados usando o bloqueio de modo harmônico sem reduzir a relação de coincidência-para-acidental (carro) – que poderá abrir caminho para informação quântica de alta velocidade, multi-canal tecnologias.

Para demonstrar o impacto e a viabilidade do domínio de frequência, controle de Estados QFC deve ser realizado em maneiras de alvo, garantindo a coerência do estado e transformações altamente eficientes. Para satisfazer tais requisitos, usamos filtros programáveis em cascata e moduladores de fase – componentes estabelecidos na indústria de telecomunicações. Filtros programáveis podem ser usados para impor uma amplitude espectral arbitrária e as máscaras de fase os fótons única, com uma resolução suficiente para abordar cada modo de frequência individualmente; e moduladores de electro-óptica fase impulsionados por geradores de sinal de rádio-frequência (RF) facilitam a mistura dos componentes de frequência²¹.

O aspecto mais importante deste esquema de controle é que opera em todos os modos de quântica dos fótons simultaneamente em um único modo espacial, usando elementos de controle único. Aumentando a dimensionalidade do estado quântico não conduzirá a um aumento da complexidade da instalação, em contraste com esquemas de emaranhamento do caminho - ou tempo-bin. E também todos os componentes são reconfigurável externamente (ou seja, as operações podem ser alteradas sem que altera a configuração) e usar a infra-estrutura de telecomunicações existente. Assim, existentes e futuros desenvolvimentos no campo do processamento óptico ultra rápido podem ser transferidos diretamente para o controle evolutivo de estados quânticos no futuro.

Em resumo, a exploração do domínio de frequência por QFCs oferece suporte a geração de altas taxas de complexos estados quânticos e seu controle e, assim, é well-suited para o aproveitamento dos Estados complexos para as tecnologias de quântico prático e escalável.

Protocolo

1. a geração da frequência alta dimensão-bin enredada Estados via excitação pulsada

1. Seguindo o esquema descrito na Figura 2 (estágio de geração), conecte cada componente usando polarização-mantendo as fibras ópticas (para melhor estabilidade ambiental).
2. Conectar uma fonte de alimentação para o modulador de amplitude de electro-óptica e aplicar um DC offset de tensão, ajuste o valor de deslocamento até a potência óptica transmitida através dele é aproximadamente metade (medido usando um medidor de potência óptica), por exemplo., de tal forma que um pico valor de transmissão de 2 mW é reduzida para metade de 1 mW.
3. Meça o comprimento aproximado de cavidade externa. Calcular o espaçamento de modo externo cavidade usando a relação,
   
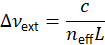
   onde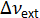 é o modo de cavidade externa espaçamento, c é a velocidade da luz no vácuo, 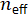é o índice eficaz do meio de cavidade, e L é o comprimento da cavidade externa. Por exemplo, para uma cavidade de 20m compreendida de fibra com um índice de refração eficaz de 1,46, o espaçamento de modo aproximado cavidade seria 10,2 MHz.
4. Ligue o EDFA iniciar lasing.
5. Insira o fotodiodo rápido a instalação o acoplador de cavidade ou outras portas de anel. Conecte o sinal do fotodiodo para um osciloscópio para observar a intensidade do campo de excitação no domínio do tempo.
6. Definir a resolução de tempo do osciloscópio de < 100 ps (através do botão de escala horizontal) a fim de resolver os pulsos ns-escala. Neste passo, sem o modulador ativado, a saída no osciloscópio mostrará operação pulso instável com uma qualidade baixa, trem de pulso de ruído elevado.
7. Conecte um gerador de função para o modulador de amplitude de electro-óptica. Defina a frequência da saída do gerador de função para o espaçamento de modo (aproximado) cavidade externa encontrada acima (ou uma harmônica do mesmo). Este sinal executa o modo de bloqueio. Escolha uma forma de onda (Retangular) de pulso ou para modulação de amplitude da onda de seno. Liga o gerador de função.
8. Sintonize a frequência de gerador de função RF e DC deslocamento para otimizar e estabilizar a forma do trem de pulso no osciloscópio. Se for usado um sinal pulsado de condução, Otimize seu ciclo de dever.
9. Ajustar manualmente o ganho EDFA para reduzir (ou aumentar) a intensidade do pulso ao regime onde as propriedades dos fótons gerados são como desejado pelo usuário (o carro é uma métrica útil aqui - veja abaixo para obter detalhes sobre sua medição). Por isso, compare os histogramas de coincidência respectivos gerados pela interface visual que vem com o sistema eletrônico de cronometragem.
10. Alimente o canal de sincronização de eletrônica de sincronismo com o sinal de trem de pulso (detectado pelo fotodiodo) ou o sinal de bloqueio de modo RF para sincronizar os detectores de fóton único com a geração de par de fótons.
11. Para aumentar a taxa de geração das QFCs, dirigir o modulador de bloqueio de modo à maiores harmônicos de espaçamento de frequência a cavidade externa, enquanto aumentando simultaneamente o ganho EDFA para garantir a mesma energia por pulso — Isso mantém o fóton emparelhar o carro enquanto aumentar a taxa de produção de par (Figura 3). Por isso, aumente a frequência de saída de gerador de função e ganho EDFA respectivamente.

2. controle da frequência-bin High-dimensional enredada Estados

1. Seguindo o esquema descrito na Figura 2 (estágio de controle), conecte todos os componentes, utilizando fibras de polarização-manutenção. A partir do filtro do entalhe no regime de geração, liga em série o primeiro filtro programável, modulador de fase e segundo filtro programável. Finalmente, ligar os detectores de fóton único, para fins de medição.
2. Operação do filtro programável
   Nota: Dependendo da aplicação/medição específica sendo executada, os parâmetros de controle do QFC irão variar e as máscaras de fase e amplitude aplicadas para os modos de frequência devem ser determinadas em conformidade. A máscara de amplitude pode ser usada para atenuar ou bloquear determinados modos de frequência e a máscara de fase pode dar uma mudança de fase arbitrários em cada modo.
   1. Determine as máscaras necessárias para a aplicação desejada/medição.
   2. Através do filtro programável interface visual²², definir a amplitude dos canais modo frequência desejada e atenuar todas as outras.
   3. Da mesma forma, aplica a máscara de fase (fase aplicada para os canais indesejados é sem importância, como eles são inteiramente atenuados). Controle o filtro programável com uma interface visual, onde as frequências desejadas são selecionadas.
3. Operação de modulação de fase
   1. Usando a modulação de fase, impulsionada por um sinal periódico, dividir cada componente espectral em faixas laterais-espaçadas pela frequência do gerador de sinal que está dirigindo o modulador de fase. Use isto para misturar vários modos de frequência quântica diferentes, análogos com divisores de feixe espaciais em esquemas de caminho-emaranhamento. No regime quântico, modulação de fase de electro-óptica é considerada um quantum dispersando operação²³.
   2. Determinar os modos de frequência alvo (dependente de e a medição/transformação sendo executada) e calcular o padrão de tensão (frequência e amplitude para um gerador de onda senoidal) para otimizar o desejado 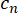valores (veja abaixo para alguns detalhes sobre isso).
   3. Ligue o gerador de sinal para o amplificador de RF usando cabos de baixa perda (tais como cabos SMC). Conecte a saída do amplificador de RF do modulador de fase, também usando os cabos de RF adequados. Uma vez que todos os fins de RF estão conectados e corretamente finalizado, viés do amplificador de RF.
   4. Certifique-se de que o amplificador de RF tem potência suficiente para conduzir o modulador de fase de electro-óptica com tensão suficiente para cumprir as condições de mistura desejadas — estas são da ordem de vários 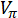(a tensão de meia onda do modulador de fase). Além disso, certifique-se que os cabos de RF e conectores são adequados para a faixa de largura de banda e frequência do sinal de condução.
   5. Definir o gerador de sinal de RF (que está dirigindo o modulador de fase) em uma frequência que se sobrepõem os modos desejados com os lado-bandas criados (por exemplo., 33 GHz).
   6. Liga o gerador de sinal para misturar os modos de frequência.
   7. Para verificar que a modulação correta é aplicada, enviar um laser assemelhace através do modulador de fase e verifique se o espectro de saída corresponde à modulação pretendido utilizando um analisador de espectro óptico (os parâmetros de modulação podem ainda ser otimizado, ver notas).
      Nota: Otimizando a mistura de modos de frequência (determinar a frequência de funcionamento ideal e a amplitude) é altamente dependente do regime de misturando desejado, experimentar sendo executada e dimensionalidade do estado . Se possível, os esquemas de misturando devem misturar modos de perto o modo de frequência inicial (em bandas laterais de baixo-inteiro) para aumentar a eficiência da mistura. Por exemplo, se 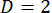, a mistura é recomendada para ocorrer no meio do caminho entre os modos de duas frequências (assim, a modulação de fase deve ser conduzida em uma frequência que tem um número inteiro múltiplo igual à metade da frequência de modo quântico espaçamento ou livre faixa espectral (FSR)). No entanto, para 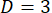, mistura é recomendado para ocorrer no modo de frequência de centro (fase modulação deve ser conduzida em uma frequência com um número inteiro múltiplo igual para o FSR). Por exemplo, com 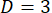e microcavidade 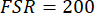GHz, a modulação de fase, sinal de condução é definida como 33,33 GHz tal que a 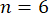lateral sobrepõe-se com os modos de frequência vizinha - deixando também intensidade suficiente no centro modo de frequência. Isso resulta na sobreposição de bandas laterais vizinhas modos 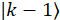, 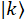e 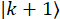no modo de frequência centro 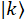. Figura 4a visualiza um exemplo do processo de modulação e os coeficientes de banda lateral. Cada modo de frequência sofre a mesma modulação de fase e cria a mesma distribuição de banda lateral, mas centrado sobre o modo de frequência original (figura 4a). Para um modo de frequência simples, as amplitudes de banda lateral são calculadas como os coeficientes de uma série de Fourier²⁴,
      
      onde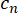 é a amplitude, transferida para o lateral -th, 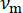é a frequência com que o modulador de fase é conduzido, 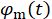é o padrão de modulação de fase (periódica com frequência 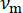), e 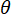é o argumento da função de modulação periódica (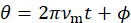). Para um sinal senoidal de condução, 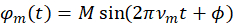, as amplitudes de faixa lateral são descritas pela expansão Jacobi-Anger,
      
      
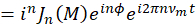
      onde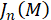 é o ordem -ésima função de Bessel do primeiro tipo avaliado em 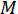e 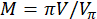é a mudança de fase máxima (onde 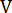é a amplitude da tensão do sinal de condução do Tom simples).

3. processamento da frequência-bin High-dimensional enredada Estados

1. Espectro de fóton único
   1. Inserir um detector de fóton único após a filtragem do campo de excitação do QFC, na saída de um filtro programável.
   2. Através do software de computador filtro programável, varra a largura de banda do filtro completo programável usando uma máscara de amplitude de filtro passa-banda estreita, taxas de contagem de fótons de medição em função da frequência. Por exemplo, se um visual interface/controle script em MATLAB é usado (que é conectada com o controle de filtro programável e cronometragem eletrônica), insira os valores de largura de banda do filtro desejado e passo número e clique em "Executar". Certifique-se de tempo suficiente de integração para obter adequado fotão conta.
   3. Para reconstruir o espectro desses dados, plotagem (por exemplo, usando um script Matlab) as taxas de contagem de fótons contra o comprimento de onda correspondente (centro do filtro passa-banda) onde foram adquiridas.
2. Medição de coincidência
   1. Para realizar uma medição de coincidência, dividir e rotear o sinal e fótons tensor para separar detectores de fóton único. Se o filtro programável tem várias portas, usá-lo para realizar a separação. Caso contrário, inserir uma comprimento de onda densa divisão multiplexador (DWDM) antes dos detectores de fóton único e usar isso para rotear os fótons.
   2. Selecione um sinal e tensor par (por exemplo, as linhas segunda ressonância em relação à frequência de excitação, sinal-2 e tensor-2) usando o programável do filtro (através da interface do software fornecido) e encaminhá-los aos dois detectores de fóton único separado. Por exemplo, para o software WaveManager, clique o Flexgrid sub-menu, clique em "Adicionar" e digite a porta de saída e o comprimento de onda para o canal escolhido²².
   3. Registrar o tempo de chegada do sinal e tensor fótons usando o conversor tempo-digital. Partir destas medições, calcule o tempo de atraso entre os dois fótons. Plotar um histograma (por exemplo, usando um script Matlab) coincidência conta um time-delay entre o sinal e tensor — isto fornece uma medida da coincidência.
      Nota: A métrica de carro compara o número de contagens de verdadeira coincidência de pares de fótons gerados com as contagens de coincidência acidental decorrentes de processos de fótons multi e contagens escuras.
   4. Desde a medição de computado-acima, registrar o número de contagens no pico do centro (coincidências decorrentes de fótons produzidos no mesmo pulso, centrado em torno do zero atraso, 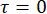) — que é o valor de coincidência.
   5. Gravar o número médio de contagens em cada lado do pico (coincidências de fótons produziram em diferentes pulsos, onde é um múltiplo do pulso treinar muito tempo, i. e., o inverso da taxa de repetição de pulso), que é o valor acidental.
      Nota: O carro é simplesmente a relação entre esses dois valores (valor de valor/acidental coincidência).
3. Reconstrução de matriz densidade
   Nota: O processo de reconstrução de matriz densidade depende de vários parâmetros do estado quântico: a dimensionalidade dos fótons, o número de fótons, e quais modos estão sendo medidos. O número de medições crus necessário é igual a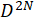, ondeé a dimensionalidade e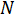é o número de fótons. Assim, por exemplo, um par de dois fotões com uma dimensionalidade dos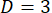exigirá 81 medições. Este protocolo irá delinear o processo geral para a reconstrução da matriz densidade, com exemplos para um par de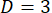fótons de modo de frequência.
   1. Determine um conjunto de vetores de base para o estado desejado e um conjunto de vetores de projeção (veja abaixo para obter detalhes sobre como escolher adequadamente estas).
   2. Com uma medição de coincidência, use ou um filtro programável ou um sinal de rota DWDM e fótons tensor para separar detectores de fóton único.
   3. Através do controle de software de filtro programável, selecione os modos de frequência desejada e atenuar todas as outras. Defina a fase valores de máscara para realizar cada vetor de onda de projeção individualmente e gravar uma medição de coincidência. É importante permitir que o mesmo tempo de integração entre projeção diferentes contagens de coincidência.
   4. Usando um script personalizado computador, calcule a matriz de densidade dos fótons usando as medidas de contagem crua coincidência de cada vetor de onda de projeção (veja abaixo para detalhes relevantes computacionais).
      Nota: Ao determinar os vetores de base para a medição de matriz de densidade, eles devem abrangem o espaço do estado. Para o caso de exemplo, são os vetores de base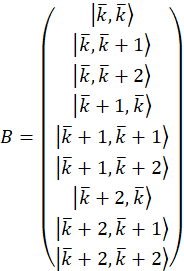
      
      Para um estado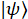 , a matriz de densidade descreve o estado quântico,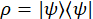
      
      A matriz de densidade para qualquer sistema físico real deve ser uma matriz definida positiva e Hermitiana - mas devido ao ruído, isto pode nem sempre ser o caso. No caso de exemplo, com a base escolhida, o vetor de onda para o estado ideal màxima emaranhados de frequência pode ser representada como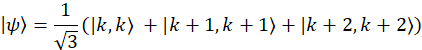
      
      e assim, a matriz de densidade teórica seria:
      
      São efectuadas medições de projeção de uma série de projeção wavevectors,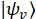 . Coincidência de contagens para cada projeção são dadas como,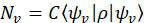
      
      onde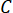 é uma constante (veja definição abaixo).
   5. Escolher um conjunto ortogonal de 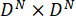, normalizado matrizes, 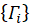, tal que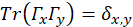
      
      onde é o traço, é a dimensão, 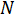é o número de fótons, e 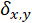é a função delta de Kronecker. Estas matrizes podem ser construídos usando o especial unitário SU () geradores (das quais existem 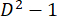), juntamente com a matriz de identidade, através de todos os possíveis tensor produto combinações²⁵. Veja abaixo as matrizes ortogonais do caso exemplo.
   6. Reconstruir a matriz de densidade, 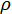, via as seguintes relações,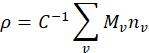
      
      
      
      
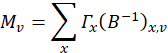
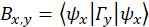
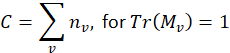
      onde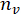 é o fóton conta para o vetor de projeção -th, 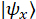são os vectores de projeção (ver próximo passo), ond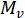e e são calculados de acordo com a definição da equação.
      Nota: São wavevectors de projeção para o caso de exemplo,
      
      
      
      
      
      
      
      
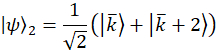
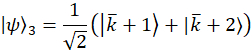
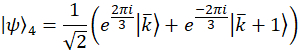
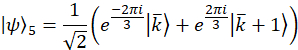
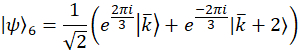
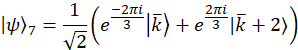
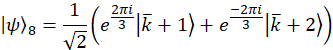
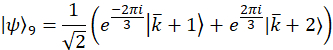
      Experimentalmente, estes wavevectors são realizados por transmitir a mudança de fase apropriada em cada modo através do filtro programável. Referem-se a anterior publicação²⁵ para discussão sobre vetores de projeção. O conjunto ortogonal de matrizes,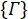 exemplo de caso são escolhidos primeiro usando os geradores SU(3) junto com a matriz de identidade,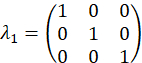
      
      
      
      
      
      
      
      
      
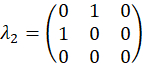
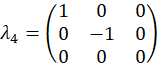
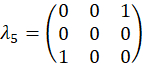
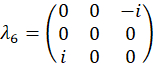
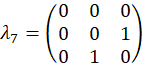
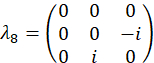
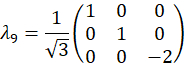
      e são computados como,
      
   7. Para uma discussão mais aprofundada da reconstrução do estado alta dimensão, consulte referência 25 ²⁵.

Resultados

O esquema descrito para a geração e o controle dos Estados de frequência alta dimensão-bin (baseado na excitação de microcavidades não-lineares, Figura 1) é mostrado na Figura 2. Esta configuração usa componentes de telecomunicações padrão e é altamente flexível, a taxa de produção de fótons e as operações de processamento aplicadas. A Figura 3 mostra a caracterização do regime ...

Discussão

O domínio de frequência óptico, através de QFCs, é vantajoso em aplicações quântico para uma série de razões. As operações são globais, atuando em todos os Estados simultaneamente, que resulta em um projeto que não se adapta em tamanho ou complexidade como os aumentos de dimensionalidade do estado. Isto é realçado como os componentes podem ser reconfigurada on-the-fly sem alterar a configuração e são capazes de ser integrado no chip explorando existentes e/ou desenvolvimento de infra-estruturas de tele...

Materiais

Name	Company	Catalog Number	Comments
Superconducting Nanowire Single-Photon Detector System	Quantum Opus	Opus One
Electro-optic phase modulator	EO-Space	Low loss model
Programmable filter	Finisar	WaveShaper 4000s
Timing electronics	PicoQuant	HydraHarp 400
Micro-ring resonator			200 GHz FSR micro-ring resonator made from high refractive index glass. See Ref. 24 for platform details.
Erbium-doped fiber amplifier	Keopsys	PEFA-SP-C-PM-27-B202-FA-FA
Electro-optic amplitude modulator	Oclaro	SD40
RF tone source	Rohde & Schwarz	SMP 04
RF tone amplifier	RF-Lambda	RFLUPA27G34GA
Function generator	Tetronix	AFG 3251
Isolator	General Photonics	NISO-S-15-SS-FC/APF
Oscilloscope	Tetronix	TDS5052B
Photodiode	Finisar	XPDV 50 GHz
DWDM	OptiWorks	DWFUQUMD08BN
Power supply	Madell	CA18303D