Method Article
Introducción al procesamiento, ajuste e interpretación de datos de absorción transitoria
En este artículo
Resumen
Este protocolo es una puerta de entrada para principiantes en el procesamiento, ajuste e interpretación de espectros de absorción transitoria. El enfoque de este protocolo es la preparación de conjuntos de datos y el ajuste utilizando tanto la cinética de una sola longitud de onda como el análisis de la vida útil global. Se discuten los desafíos asociados con los datos de absorción transitoria y su ajuste.
Resumen
La espectroscopia de absorción transitoria (TA) es un potente método espectroscópico resuelto en el tiempo que se utiliza para rastrear la evolución de los procesos de estado excitado a través de cambios en el espectro de absorción del sistema. Las primeras implementaciones de la AT se limitaron a laboratorios especializados, pero la evolución de los sistemas comerciales llave en mano ha hecho que la técnica esté cada vez más disponible para los grupos de investigación de todo el mundo. Los sistemas modernos de TA son capaces de producir grandes conjuntos de datos con alta resolución energética y temporal que son ricos en información fotofísica. Sin embargo, el procesamiento, el ajuste y la interpretación de los espectros de TA pueden ser un desafío debido a la gran cantidad de características de estado excitado y artefactos instrumentales. Hay muchos factores que deben tenerse en cuenta a la hora de recopilar, procesar y ajustar los datos de TA para reducir la incertidumbre sobre qué modelo o conjunto de parámetros de ajuste describe mejor los datos. El objetivo de la preparación y el ajuste de los datos es reducir la mayor cantidad posible de estos factores extraños y, al mismo tiempo, preservar los datos para su análisis. En este método, los principiantes reciben un protocolo para procesar y preparar los datos de TA, así como una breve introducción a los procedimientos y modelos de ajuste seleccionados, específicamente el ajuste de una sola longitud de onda y el análisis de la vida útil global. Se comentan algunos de los problemas más comunes en la preparación de datos y los métodos para abordarlos, seguidos de un análisis de los retos y limitaciones de estos sencillos métodos de ajuste.
Introducción
La espectroscopia de absorción transitoria (TA) es una técnica espectroscópica resuelta en el tiempo que monitorea la evolución de las especies fotoexcitadas a través de cambios dependientes del tiempo en su espectro de absorción después de la excitación con un pulso de luz. Debido a que la AT es una técnica de absorción, se pueden identificar las señales espectroscópicas que surgen de estados que experimentan tanto transiciones radiativas (es decir, estados que normalmente emiten un fotón) como transiciones no radiativas (estados que normalmente no son fluorescentes y experimentan conversión interna, cruce entre sistemas o participan en fotorreacciones) y se puede seguir su evolución 1,2. Dependiendo de los detalles de la fuente de excitación y el método de detección, el TA permite el acceso a la cinética desde los femtosegundos hasta más allá de los microsegundos y desde el UV hasta el infrarrojo lejano, lo que lo convierte en una herramienta espectroscópica versátil. La comercialización de espectrómetros TA ha avanzado significativamente en las últimas décadas, lo que ha llevado a que más laboratorios e instalaciones tengan acceso a esta poderosa técnica2.
Los sistemas modernos de TA son capaces de producir grandes conjuntos de datos con alta resolución energética y temporal. Los conjuntos de datos generalmente toman la forma de una matriz 2D de valores de diferencia de transmitancia o absorbancia en función de la longitud de onda y el retardo de tiempo en relación con el pulso de excitación. Este dataset se puede ver como un mapa de calor bidimensional o un mapa topográfico tridimensional. La interpretación de estos datos se ha vuelto más compleja a medida que los investigadores se esfuerzan por incluir todo el conjunto de datos al generar los ajustes que mejor describen su sistemade interés.
Aunque el TA puede cubrir una amplia gama de longitudes de onda y escalas de tiempo, este protocolo se centra en una de sus formas más accesibles4: la espectroscopia de banda ancha en la región UV-visible impulsada por un láser pulsado de femtosegundos. En la Figura 1 se presenta un esquema 5,6 de dicho instrumento. El experimento comienza tomando un pulso del láser y dividiéndolo en dos copias. Se utiliza una copia del pulso, llamada "bomba", para excitar la muestra. Normalmente se utiliza un dispositivo como un amplificador paramétrico óptico (OPA) para transformar el pulso de la bomba a la longitud de onda de excitación deseada 5,7. La segunda copia del pulso, llamada "sonda", entra en una etapa de retardo mecánico, que puede variar el retardo de tiempo entre los pulsos de la bomba y la sonda variando la distancia que recorre el pulso. A continuación, el pulso de la sonda de una sola longitud de onda se transforma en un continuo de luz blanca utilizando un cristal de zafiro o fluoruro de calcio (CaF2)8. El pulso de luz blanca pasa a través de la muestra y su espectro se mide utilizando un detector de banda ancha, como una cámara de dispositivo de carga acoplada (CCD). Al medir los cambios en el espectro del pulso de luz blanca con y sin la bomba, se pueden medir los cambios en el espectro de absorción de la muestra inducidos por la bomba, ΔA(T). Los lectores interesados pueden dirigirse a esta útil revisión9 para obtener más información sobre el proceso de detección.
En todas las formas de espectroscopía TA, los espectros ΔA(t) se calculan tomando la diferencia entre la absorción del estado fundamental, lasonda A, y la del estado excitado, Abomba+sonda, en un retardo de tiempo dado, t, entre los dos pulsos 2,5,9,10.
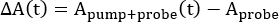 (1)
(1)
Tenga en cuenta que unasonda es equivalente al espectro de absorción en estado estacionario de la muestra y es independiente del tiempo; la resolución temporal del experimento surge del retardo entre la bomba y la sonda capturada en Abomba+sonda (t). En la Figura 2A se muestra una simulación de estos datos.
A diferencia de los espectros de absorción en estado estacionario, los espectros TA pueden tener características tanto positivas como negativas debido a la diferencia tomada en la Ecuación 1. Las características positivas son el resultado de nuevas especies absorbentes creadas por el pulso de bombeo y pueden representar estados cromóforos excitados, estados tripletes, reordenamientos geométricos, efectos de solvatación o fotoproductos en estado excitado3. En el debate se presentarán directrices generales para identificar estas características y asignarlas a las especies químicas. Las características negativas pueden surgir de la lejía en estado fundamental (GSB) o de la emisión estimulada (SE) (Figura 2B). El GSB se debe a la pérdida de población en estado fundamental después de la absorción del pulso de la bomba. Las moléculas promovidas al estado excitado ya no absorben en la misma región que su estado fundamental; por lo tanto, se absorbe menos pulso de la sonda, y la diferencia en la Ecuación 1 puede ser negativa en esa región. El GSB se caracteriza por tener la misma forma espectral que la de la absorción del estado fundamental pero con un signo opuesto. Las señales SE son el resultado de la emisión de una especie en estado excitado estimulada por el pulso de la sonda3. La emisión de estas especies da como resultado que llegue más luz al detector, lo que equivale a tener menos absorción en esas longitudes de onda. La señal SE tendrá una forma espectral similar a la del espectro de emisión espontánea de la especie, pero con un signo negativo y una ponderación de frecuencia diferente10.
Además de la información sobre las especies en estado excitado, los espectros de AT pueden contener una serie de artefactos y características extrañas que pueden distorsionar la dinámica subyacente y oscurecer la asignación de bandas de absorción11. El tratamiento inadecuado de estos artefactos en la preparación y análisis de los datos puede conducir a la aplicación de modelos fotofísicos inapropiados a los datos y, en consecuencia, a conclusiones engañosas11. Por lo tanto, la primera parte de este protocolo se centra en cómo procesar correctamente los conjuntos de datos de TA después de que se recopilan. El objetivo de esta sección es proporcionar a los investigadores nuevos en la AT un conjunto de pautas que ayudarán a desarrollar la intuición y el aprecio por la preparación y el procesamiento rigurosos de sus datos.
Una vez procesado un conjunto de datos, se dispone de una gran cantidad de herramientas y modelos para ajustar e interpretar los espectros con diversos niveles de complejidad y rigor10. El objetivo de la segunda sección de este protocolo es preparar al lector para aplicar el ajuste de una sola longitud de onda y el análisis global a los datos y proporcionar orientación sobre cuándo estos modelos son apropiados para describir sus datos. El software comercial ahora está disponible para preparar y tratar datos de TA, como Surface Xplorer12,13 de sistemas ultrarrápidos (descarga y uso gratuitos, consulte la Tabla de materiales). Otras alternativas gratuitas han sido lanzadas por investigadores académicos, como Glotaran14. Glotaran es un programa de software libre desarrollado para el análisis global y de objetivos de datos de espectroscopía y microscopía resueltos en el tiempo. Sirve como interfaz gráfica de usuario (GUI) para el paquete R TIMP14. Además, los usuarios pueden utilizar lenguajes de programación como Python para escribir sus propios códigos que lleven a cabo el análisis. Cada una de estas soluciones de software y programación tiene características positivas que las convierten en importantes contribuciones. Para el propósito de este estudio, podemos presentar solo un software para el componente visual de esta actividad. Una discusión en profundidad de cada software de ajuste está más allá del alcance de este artículo.
Este artículo proporciona un procedimiento paso a paso para (1) procesar datos de AT, (2) ajustar datos de TA utilizando cinética de longitud de onda única y análisis global, y (3) extraer datos y ajustarlos a otros modelos. Se incluye un conjunto de datos representativos de AT para que el lector los utilice como práctica (Archivo Suplementario 1 y Archivo Suplementario 2). Los datos son una medición de una muestra de 165 μM de 1,4-bis(5-feniloxazol-2-il)benceno (POPOP) en etanol excitado a 330 nm y recogido en un rango de -5 ps a 5,5 ns. Además, se recolectó una muestra "en blanco" que contenía solo etanol y ninguna muestra en las mismas condiciones experimentales en un rango de -5 ps a 5 ps, que se utiliza en la preparación de los datos para el ajuste (paso 1). Los espectros se recogieron utilizando un espectrómetro de absorción transitoria ultrarrápida. La muestra se contuvo en una cubeta de 2 mm de longitud y se sometió a agitación constante. El procedimiento de procesamiento y ajuste descrito se basa en el software Surface Xplorer que ajusta los datos en el formato *.ufs, y que en lo sucesivo se denominará el "programa de ajuste". Existen programas para convertir conjuntos de datos en otros formatos a archivos *.ufs15. Aunque los detalles de este protocolo son específicos de Surface Xplorer, los pasos que siguen son generalizables a cualquier paquete de software, comercial o casero. Además, los resultados del procesamiento de datos pueden extraerse y ajustarse utilizando estos otros paquetes de software. Un fichero de información justificativa (Fichero Complementario 3) proporciona asesoramiento adicional sobre la instalación.
Protocolo
1. Preparación de los datos para el ajuste
- Cargue el conjunto de datos SAMPLE en el software de ajuste. Los datos aparecerán como se muestra en la Figura complementaria 1.
- Cuando la luz de excitación dispersa esté presente dentro de la ventana de detección óptica del experimento, utilice la opción Restar luz dispersa (Figura complementaria 2). Si no hay ninguna luz de excitación dispersa en los datos, continúe con el paso 1.5.
NOTA: La luz dispersa se observa con mayor frecuencia cuando la longitud de onda de excitación cae dentro de la ventana óptica. La luz dispersa aparece como una característica negativa nítida (blanqueadora) en la longitud de onda de excitación (o algún orden de difracción, o longitud de onda producida en el OPA) que no varía con el tiempo. - Haga clic en el menú Superficie y, a continuación, haga clic en la opción Restar luz dispersa (Figura complementaria 2). Aparecerá una nueva ventana.
- En la nueva ventana, haga clic en los botones de flecha para establecer el número de espectros de fondo en promedio (Figura complementaria 3) para realizar la corrección de fondo. El uso de diez espectros proporciona un buen punto de partida y el número se puede ajustar como se desee. Haga clic en Aceptar para realizar la resta (continúe con el paso 1.7).
NOTA: Los espectros de fondo se extraen de los primeros espectros presentes en el conjunto de datos y luego avanzan temporalmente utilizando tantos espectros de fondo como sea necesario para proporcionar un promedio de la señal de fondo; Sin embargo, si se usan demasiados, se comenzarán a usar espectros que contienen la señal de interés, así que no use demasiados. Con datos de ventana de tiempo larga, es posible que la función de dispersión no aparezca al final de la ventana de tiempo de los datos. Esto puede ocurrir si la ventana de tiempo supera el tiempo de integración de la cámara, u otros motivos, en función de cómo se construya el experimento de TA. Para corregir esto, se puede utilizar la opción de establecer rango de tiempo como se describe en el Archivo complementario 3. - Para los datos en los que no hay luz dispersa dentro de la ventana óptica, haga clic en el menú Superficie y, a continuación, haga clic en la opción Restar fondo .
- En la ventana que aparece, haga clic en los botones de flecha en la parte inferior derecha para que "Número de espectros" promedie (elija 10) y haga clic en Aceptar.
NOTA: Los espectros de fondo en esta opción funcionan igual que en la opción "Restar luz dispersa". Comenzar con diez espectros proporciona un buen promedio. Se pueden usar más espectros, pero se debe tener cuidado de no usar demasiados para evitar incluir espectros que contengan señales de interés. El manual de usuario de Surface Xplorer describe las diferencias en la corrección aplicada para la opción "Restar luz dispersa" frente a la opción "Restar luz dispersa". la corrección más básica de "Restar fondo". Es importante aplicar la corrección adecuada para el artefacto16. - Los datos cerca de los bordes de la ventana óptica pueden tener una relación señal-ruido muy baja como resultado de la forma del espectro de la sonda y/o de que la muestra absorbe demasiada luz blanca. Los datos ruidosos en estas regiones dificultan el análisis. Elimine estas partes inútiles del espectro. Haga clic en las longitudes de onda finales del espectro (mosaico inferior izquierdo), escriba nuevos valores (Figura complementaria 4) y haga clic en enter. Elija un rango de longitud de onda que elimine los datos ruidosos en los bordes de la ventana. Para los datos proporcionados, el rango es de 340-680 nm.
- Finalice el ajuste de la ventana espectral al rango deseado de longitudes de onda. Haga clic en el menú Superficie y, a continuación, haga clic en Recortar (Figura complementaria 5). Aparecerá una ventana emergente.
- Haga clic en Aceptar. Haga clic en el menú Archivo , luego haga clic en Guardar archivo como. A continuación, haga clic en Aceptar. Cierre este conjunto de datos.
NOTA: Tenga cuidado al recortar, ya que la función recortará los datos a lo largo de los ejes de longitud de onda y retardo de tiempo, eliminando todos los demás datos. Asegúrese de que la ventana de retardo de tiempo contenga la parte de los datos que se van a conservar. Además, se recomienda encarecidamente guardar los datos recortados como un archivo nuevo y debidamente etiquetado para dejar intacta la superficie de datos sin procesar como copia de seguridad.
- Haga clic en Aceptar. Haga clic en el menú Archivo , luego haga clic en Guardar archivo como. A continuación, haga clic en Aceptar. Cierre este conjunto de datos.
- Para los datos recopilados en las escalas de tiempo fs o ps, se debe aplicar una corrección de chirrido. Abra la superficie de datos con solo el disolvente o sustrato (sin muestra) tomado en la misma configuración experimental que los datos. Este ejemplo se denomina ejecución de experimento "en blanco". Realice el mismo conjunto de pasos en los datos "en blanco" (del paso 1.2 al paso 1.8) que se realizaron en los datos de muestra.
NOTA: Se recomienda encarecidamente que un experimento "en blanco" de este tipo se ejecute en las mismas condiciones que la muestra pero con una ventana de tiempo más corta (por ejemplo, ~ −5 ps a 5 ps) para garantizar un alto número de puntos alrededor del tiempo cero. Esta corrida "en blanco" debe consistir solo en solvente o sustrato, dependiendo del tipo de muestra, y se utiliza para establecer la curvatura del chirrido. La preparación de la "pieza en blanco" hasta este punto debe seguir la misma corrección de fondo y recorte que los datos de muestra. Si no se ejecutó un "espacio en blanco", la corrección del chirrido se puede realizar directamente en el conjunto de datos. - Inicie el proceso de corrección de chirridos. En el mosaico del mapa de calor (arriba a la izquierda), haga clic en la cruz y arrastre el componente de línea vertical hasta el extremo azul del espectro. Comience en el rango de longitud de onda azul cerca del comienzo de la ventana espectral. Haga clic en el menú Cinética y, a continuación, haga clic en Ajustar respuesta al disolvente.
NOTA: La respuesta de ajuste del solvente solo debe realizarse en una muestra "en blanco" que no genere ninguna señal más allá del tiempo cero. Si se intenta aplicar esta función de ajuste a un conjunto de datos que contiene datos sobre una molécula o material de interés, el programa intentará ajustar los datos en lugar de la IRF (función de respuesta del instrumento). En el caso de las muestras "en blanco", la única señal presente debe ser un artefacto coherente que surja de la modulación de fase cruzada. La modulación de fase cruzada ocurre solo donde los haces de la bomba y la sonda se superponen y, por lo tanto, proporciona un rastro de la curvatura del chirp que se puede ajustar utilizando la opción "Ajustar respuesta al solvente". La colocación manual de puntos será necesaria para los datos que no tengan un "espacio en blanco" que los acompañe para su corrección y se describen con más detalle en el Archivo Complementario 3. - Se abre una nueva ventana "Ajustar respuesta al disolvente". Haga clic en el botón Ajustar (Figura complementaria 6). El ajuste generará un ajuste a la función de respuesta del instrumento utilizando la primera y segunda derivadas de un gaussiano. Haga clic en el botón Guardar , luego haga clic en x para cerrar la pantalla.
NOTA: La línea roja ajustada debe coincidir bien con los puntos de datos (cuadrados huecos azules) en todo el rango de tiempo, lo más importante es la característica grande que se ve cerca del tiempo cero (0.1-2.0 ps). El ajuste tendrá el mayor éxito si hay un gran número de puntos alrededor del tiempo cero, lo que se puede lograr utilizando una ventana de retardo de tiempo corta para el experimento "en blanco" y reteniendo un gran número de puntos. Si el ajuste no parece coincidir bien con los puntos de datos, marque la casilla "Agregar gaussiano (R0)" y vuelva a intentar el ajuste. Esta opción agregará una suma de la gaussiana a la primera y segunda derivadas y puede ajustarse mejor a la forma de la característica IRF en esta longitud de onda. Si el accesorio de respuesta al disolvente sigue sin capturar la señal IRF, seleccione una longitud de onda diferente. - Realice este proceso (pasos 1.10-1.11) al menos cinco veces, ya que se requerirán cinco puntos para corregir correctamente un chirrido. Los puntos deben estar espaciados a lo largo de toda la ventana espectral si es posible. Es posible que algunos disolventes/sustratos no generen una señal observable en partes de la ventana espectral, dependiendo de las condiciones experimentales. Se pueden agregar/usar más puntos según sea necesario para producir un ajuste aceptable. Cuando haya terminado, cierre el conjunto de datos "en blanco".
NOTA: Cada punto guardado se escribe en un archivo de Excel en la carpeta de trabajo como una nueva fila tan pronto como el usuario hace clic en Guardar. Si se guarda un punto no deseado, el punto se puede eliminar del archivo de Excel eliminando la fila del punto no deseado. - Vuelva a abrir el conjunto de datos recortado y sustraído en segundo plano. Haga clic en el menú Superficie , luego haga clic en la opción Corrección de chirrido . Aparecerá una nueva pantalla con tres ventanas y un menú en la parte inferior derecha (Figura complementaria 7).
- Agregue la corrección de chirrido que se acaba de crear. Haga clic en la opción Agregar desde archivo , seleccione el archivo de Excel que termina en "ajustar coeficientes" y haga clic en Aceptar. El ajuste de corrección de chirridos ahora se muestra en la ventana superior izquierda como una línea negra con marcadores X (Figura 8 suplementaria).
NOTA: La corrección del chirrido se muestra como una línea continua; los marcadores X a lo largo de la línea son los puntos generados a partir del proceso de respuesta al disolvente de ajuste. Los puntos se pueden agregar manualmente ajustando el punto de mira y haciendo clic en Agregar. Los puntos también se pueden eliminar resaltándolos y pulsando Eliminar. Otros puntos se pueden editar a mano escribiendo valores en la lista en la parte inferior derecha. Finalmente, si se desea, la corrección actual también se puede guardar como un archivo para su posterior reutilización usando el botón Guardar en archivo . - Haga clic en el botón Vista previa de la corrección del chirrido . Esto aplica temporalmente la corrección de chirrido. Observe la corrección en la ventana superior izquierda para asegurarse de que los datos se han aplanado temporalmente y no se puede observar más curvatura.
- Si está satisfecho con la corrección del chirrido, haga clic en el botón Aplicar y salir . Si no está satisfecho, repita los pasos 1.10-1.14, eligiendo más (o diferentes) longitudes de onda para el ajuste de la corrección del chirp hasta obtener una corrección satisfactoria.
NOTA: Al aplicar la corrección de chirrido, se ajustará el tiempo cero a la línea enderezada tal como aparece en la vista previa. Puede haber alguna desalineación temporal entre el "espacio en blanco" y la superficie de datos.
- Si está satisfecho con la corrección del chirrido, haga clic en el botón Aplicar y salir . Si no está satisfecho, repita los pasos 1.10-1.14, eligiendo más (o diferentes) longitudes de onda para el ajuste de la corrección del chirp hasta obtener una corrección satisfactoria.
- Haga clic en el menú Archivo , luego haga clic en Guardar archivo como. Escriba un nombre adecuado para el archivo para indicar que se ha aplicado una corrección de chirrido. A continuación, haga clic en Aceptar.
- Es posible que algunas entidades de dispersión de los datos no se eliminen por completo al realizar la resta en segundo plano. Estas características afectan al ajuste y producen resultados de ajuste erróneos. Localice cualquiera de estas características en los datos que deben eliminarse. La característica de dispersión se puede identificar más fácilmente en la región de tiempo negativa.
- En el mosaico del mapa de calor superior izquierdo, haga clic y arrastre la cruz a la región de tiempo negativa. Manteniéndose dentro de la región de tiempo negativa, utilice el punto de mira para determinar las longitudes de onda en las que comienza y termina la entidad de dispersión. Tenga en cuenta el rango de longitud de onda de la entidad de dispersión (para el dataset proporcionado, el rango de características es de 654 nm a 672 nm).
NOTA: Al determinar si se debe eliminar una entidad, arrastre la cruz horizontal hacia arriba y hacia abajo a través de los ejes de tiempo para visualizar el rango espectral de la entidad. Las características de dispersión suelen tener trazas cinéticas de una sola longitud de onda muy ruidosas, por lo que el rango espectral de la característica también se puede verificar utilizando las trazas cinéticas.
- En el mosaico del mapa de calor superior izquierdo, haga clic y arrastre la cruz a la región de tiempo negativa. Manteniéndose dentro de la región de tiempo negativa, utilice el punto de mira para determinar las longitudes de onda en las que comienza y termina la entidad de dispersión. Tenga en cuenta el rango de longitud de onda de la entidad de dispersión (para el dataset proporcionado, el rango de características es de 654 nm a 672 nm).
- Comenzando con la longitud de onda inferior (azul) (es decir, 654 nm), haga clic en la longitud de onda del extremo derecho del espectro (mosaico inferior izquierdo) y escriba el valor de la extensión de entidad inferior (azul).
- Recorta los datos haciendo clic en el menú Superficie y, a continuación, haz clic en Recortar. Haga clic en Aceptar en el menú emergente. Guarde los datos recortados con un nombre de archivo único para indicar de qué lado de los datos se trata (se recomienda azul o izquierdo). Cierre el archivo.
- Abra el archivo con la corrección de chirp aplicada guardada en el paso 1.16. Continúe hasta la extensión de longitud de onda más alta (roja) de la entidad. Haga clic en la longitud de onda del extremo izquierdo del espectro (mosaico inferior izquierdo) y escriba el valor de la extensión superior de la entidad.
- Recorta los datos haciendo clic en el menú Superficie y, a continuación, haz clic en Recortar. Haga clic en Aceptar en el menú emergente. Guarde los datos recortados con un nombre de archivo único para indicar de qué lado de los datos se trata (se recomienda rojo o derecho).
- Combine los dos archivos haciendo clic en el menú Archivo , luego haga clic en Combinar varias superficies. En la nueva ventana, seleccione ambos lados de los datos (es decir, Derecha e Izquierda o Azul y Rojo). Use ctrl + clic para seleccionar cada archivo. Verifique que ambos archivos estén seleccionados en el cuadro "Nombre de archivo:", luego haga clic en Aceptar en la parte inferior derecha. Cuando finalice la barra de progreso, los datos se habrán combinado.
NOTA: Se puede combinar cualquier número de archivos de esta manera. Los datos se pueden unir a través de múltiples cortes tanto en el eje de tiempo como en el de longitud de onda. - Haga clic en el menú Archivo , luego haga clic en Guardar archivo como y elija un nombre de archivo único para indicar que está combinado (se recomienda Combinado o Compuesto). A continuación, haz clic en Aceptar para guardar el archivo.
NOTA: Consulte la sección 3 para obtener información sobre cómo guardar datos de la ventana de datos sin procesar para su posterior visualización y trazado. Los datos del mapa de calor (mosaico superior izquierdo) deberían aparecer como en la Figura 3 y ahora están listos para ajustarse. La visualización de los espectros representativos, como se muestra en la Figura 3, se describe en el paso 3.1.2.
2. Realizar un ajuste
- Cargue la superficie de datos correctamente preparada.
- Decida qué ajuste se realizará y muévase a la sección apropiada.
NOTA: Este protocolo presenta dos opciones de ajuste de datos: el paso 2.3 presenta el ajuste de trazas cinéticas de una sola longitud de onda, y el paso 2.4 presenta el ajuste de análisis global. - Ajuste de una sola longitud de onda
- Para configurar un solo ajuste cinético, mueva el cursor (ya sea en los mosaicos superior o inferior izquierdo) a la longitud de onda deseada. Haga clic en el menú Cinética , luego haga clic en Ajustar cinética. Para el conjunto de datos proporcionado, comience con 632 nm.
- En la nueva ventana que se abre (Figura suplementaria 9), observe que los parámetros de ajuste principales y los valores de inicialización se establecen en la parte superior izquierda de la ventana, debajo del logotipo del programa, en el cuadro junto a esta área bajo el texto "ajuste actual @ longitud de onda".
- Haga clic en los botones de flecha para ajustar el número de tiempos de vida (es decir, el número de decaciones exponenciales utilizadas para ajustar los datos) en el cuadro "Tiempos de vida finitos". Para el conjunto de datos proporcionado, elija 2 duraciones. De una a 3 vidas son típicas como punto de partida.
- Si la señal de datos se extiende más allá de la ventana de tiempo recopilada, se debe incluir un componente de vida útil "infinita". Para hacer esto, haga clic en la casilla de verificación Usar vida útil infinita . Si los datos decaen completamente a la línea base, no marque esta casilla. Para el conjunto de datos proporcionado, no marque la casilla.
NOTA: La "vida útil infinita" permite que permanezca un desplazamiento de la señal (es decir, el programa no forzará el ajuste a decaer de nuevo a la línea de base). El uso de un componente infinito es necesario cuando la señal en esa longitud de onda no decae a la línea de base dentro del rango de tiempo del experimento. - Introduzca los valores de estimación de la vida útil y las amplitudes asociadas, el tiempo de respuesta del instrumento y el tiempo cero para facilitar el proceso de ajuste (Figura complementaria 10). Haga clic en el parámetro deseado. Haga clic en la ventana de valor, escriba un valor de estimación y, a continuación, haga clic en el botón de estimación inicial para establecer el valor. Para el conjunto de datos proporcionado, los valores de estimación adecuados son: 0 = 0 ps, IRF = 0,25 ps, A1 = 0,6, t1 = 100 ps, A2 = 0,08, t2 = 1100 ps.
NOTA: "0" es la estimación del tiempo cero, "IRF" es el tiempo de respuesta del instrumento, "A" se refiere a la amplitud de un exponencial dado (ver Ecuación 3) y "t" es la constante de tiempo de vida/tiempo. Proporcionar buenos valores de conjetura ayuda al programa a obtener un ajuste razonable. Elija valores "A" que estén dentro de los valores del rango A en el conjunto de datos. Elija valores "t" en rangos de tiempo en los que se observe un cambio significativo en la traza cinética. La mejor manera de obtener intuición sobre cómo afectan los valores de conjetura al ajuste es probar varios conjuntos de valores de conjetura y observar los ajustes que producen. Si se conocen uno o más de estos parámetros, ese parámetro se puede establecer y "fijar" para que no varíe con el ajuste (Figura complementaria 11). - Cuando se ingresen todos los parámetros de adivinación, haga clic en el botón Ajustar . En la Figura 4 se muestra un ajuste representativo.
NOTA: Al aplicar el ajuste, se rellenará la gráfica de datos con la línea de ajuste y una gráfica residual que se puede utilizar para evaluar la calidad del ajuste. Los parámetros de ajuste, como la vida útil y las amplitudes asociadas, el tiempo cero y el tiempo de respuesta del instrumento, también se rellenan en el cuadro superior izquierdo. Utilice varios parámetros de ajuste diferentes para determinar el número de tiempos de vida y la inclusión/exclusión de un componente de tiempo "infinito" que produzca el mejor ajuste a los datos. - Guarde el ajuste haciendo clic en el botón Guardar (Figura complementaria 9).
NOTA: Consulte la sección 3 para obtener información sobre cómo guardar datos de la ventana de datos sin procesar para su posterior visualización y trazado.
- Ajuste de análisis global
- Haga clic en el menú Surface y, a continuación, haga clic en la opción Componentes principales a través de SVD . Aparece una nueva ventana (Figura complementaria 12).
NOTA: La ventana superior derecha muestra las trazas cinéticas principales y la inferior izquierda muestra los espectros principales. El mosaico superior izquierdo muestra un trazado de la superficie residual creada por la diferencia entre la superficie original y una superficie creada por los componentes principales seleccionados.
trazado de la superficie residual creada por la diferencia entre la superficie original y una superficie creada por los componentes principales seleccionados. - Haga clic en los botones de flecha para establecer el "Número de componentes principales" (Figura complementaria 12). Para el conjunto de datos proporcionado, elija 15.
NOTA: Al decidir el número de componentes principales a elegir, una forma es seguir aumentando el número hasta que tanto los espectros principales como las trazas cinéticas principales se asemejen a un patrón de ruido. Otra forma de determinar cuántos componentes principales elegir es observar los valores de coeficiente de peso que aparecen a la izquierda de la leyenda en el mosaico superior derecho. Continúe agregando componentes principales hasta que este valor llegue a 0,01. En general, es aconsejable agregar algunos más más allá de esto por si acaso. Esto puede dar lugar a que se seleccionen hasta 15 o más componentes principales. - Haga clic en el botón Guardar . Los componentes principales guardados son necesarios para avanzar al siguiente paso.
NOTA: Cada componente principal es una representación de complejidad reducida de la superficie de datos original. El uso de componentes principales dará como resultado una superficie simplificada en comparación con los datos sin procesar que se analizan. Tener en cuenta la mayoría de las características principales de la superficie de datos es muy importante para obtener un ajuste preciso, por lo que es clave utilizar suficientes componentes principales para capturar esas características. El uso de más componentes principales no comprometerá el ajuste. Por lo tanto, si hay alguna duda sobre cuántos componentes principales seleccionar, use más componentes principales en lugar de menos. Tenga en cuenta que el uso de demasiados puede ralentizar el software de adaptación. - Después de guardar los componentes principales, el programa volverá a la pantalla principal y ahora se puede intentar el ajuste global. Haga clic en el menú Superficie , luego haga clic en la opción Ajuste global . Se abrirá una nueva ventana (Figura complementaria 13).
NOTA: Las trazas cinéticas principales se muestran en el mosaico superior derecho. El mosaico superior izquierdo mostrará una superficie de ajuste en comparación con la superficie sin procesar. El mosaico inferior izquierdo mostrará los espectros de diferencia asociados a la desintegración (DADS) generados por el ajuste. Finalmente, el mosaico inferior derecho es donde se pueden establecer los parámetros de ajuste, incluido el número de funciones exponenciales que se usarán y si se debe usar una función infinita.
superficie de ajuste en comparación con la superficie sin procesar. El mosaico inferior izquierdo mostrará los espectros de diferencia asociados a la desintegración (DADS) generados por el ajuste. Finalmente, el mosaico inferior derecho es donde se pueden establecer los parámetros de ajuste, incluido el número de funciones exponenciales que se usarán y si se debe usar una función infinita. - Utilice los botones de flecha junto al "número de experiencia" para establecer el número de funciones exponenciales que se incluirán en el ajuste. Si la señal de datos se extiende más allá de la ventana de tiempo recopilada, se debe incluir un componente de vida útil "infinita". Para ello, haga clic en la casilla de verificación Usar desplazamiento (Ainf). Para el conjunto de datos proporcionado, elija 2 y no haga clic en la casilla. Si los datos decaen completamente a la línea base, no marque esta casilla.
NOTA: Los parámetros de ajuste se pueden corregir antes de realizar un ajuste haciendo clic en la columna de etiqueta en el cuadro inferior derecho debajo de los coeficientes de ajuste global. La etiqueta se volverá roja y cambiará para tener un indicador (fijo) en la etiqueta. Cualquier valor escrito en el cuadro de la derecha se utilizará para ese parámetro en lugar de variarse libremente para el ajuste. Se debe tener cuidado al fijar los valores de un ajuste, ya que esto puede sesgar los resultados del ajuste. - Haga clic en el botón Ajustar . El progreso de ajuste se mostrará a través de una pequeña barra de carga en el centro de la pantalla. Una vez completado el progreso del ajuste, las ventanas se rellenarán con los datos del ajuste (Figura 5 y Figura complementaria 14). Examine visualmente los resultados de la adaptación.
NOTA: La información tanto del ajuste cinético principal como del DADS se utiliza para determinar si vale la pena guardar el ajuste o si es demasiado deficiente. Por lo general, si el ajuste de las trazas principales coincide bien con los datos y no hay características o hay muy pocas en la gráfica, se puede aceptar el ajuste. Es fácil comprobar múltiples ajustes cambiando el número de vidas y/o marcando/desmarcando el botón "Usar desplazamiento (Ainf)". Se debe aceptar el mejor ajuste producido después de verificar múltiples variaciones de los parámetros de ajuste.
gráfica, se puede aceptar el ajuste. Es fácil comprobar múltiples ajustes cambiando el número de vidas y/o marcando/desmarcando el botón "Usar desplazamiento (Ainf)". Se debe aceptar el mejor ajuste producido después de verificar múltiples variaciones de los parámetros de ajuste. - Haga clic en el botón Guardar . Esto guardará el ajuste que se muestra actualmente junto con los datos en un archivo de Excel.
NOTA: El archivo de Excel se guarda en la misma ubicación de archivo que el conjunto de datos. Si se realizan ajustes adicionales y es necesario guardarlos, sobrescribirán cualquier versión anterior. Por lo tanto, antes de generar y guardar un nuevo ajuste, asigne un nombre único a cualquier ajuste antiguo. Los parámetros guardados del ajuste incluyen solo el tiempo cero, el IRF, las duraciones y los DADS que los acompañan. Este archivo no contiene ninguna información sobre la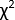 gráfica o el ajuste a las trazas cinéticas principales. El almacenamiento de las trazas cinéticas principales se describe en el paso 3.3. Consulte el paso 3.0 para obtener información sobre cómo guardar datos de la ventana de datos sin procesar para su posterior visualización y trazado.
gráfica o el ajuste a las trazas cinéticas principales. El almacenamiento de las trazas cinéticas principales se describe en el paso 3.3. Consulte el paso 3.0 para obtener información sobre cómo guardar datos de la ventana de datos sin procesar para su posterior visualización y trazado.
- Haga clic en el menú Surface y, a continuación, haga clic en la opción Componentes principales a través de SVD . Aparece una nueva ventana (Figura complementaria 12).
3. Extracción de datos en bruto y ajustes del software de ajuste para el trazado
NOTA: Los datos sin procesar o los ajustes producidos a partir de un ajuste de una sola longitud de onda o el análisis global se pueden exportar a archivos csv que se pueden abrir en una variedad de otros programas.
- Extracción de datos sin procesar para el trazado
- Para exportar el mapa de calor del conjunto de datos, haga clic en el menú Archivo y, a continuación, haga clic en Exportar a CSV (Figura complementaria 15). Esto abrirá una ventana, haga clic en Aceptar para guardar el archivo csv en el mismo directorio que el archivo de datos abierto con el mismo nombre que el archivo de datos.
NOTA: Alternativamente, los datos sin procesar se pueden exportar haciendo clic con el botón derecho en la ventana del mapa de calor y haciendo clic en Exportar datos al portapapeles. Esto guardará temporalmente los datos para que puedan pegarse en un documento de software de la elección del usuario. Pegue los datos en un archivo de Excel y, a continuación, guárdelos. - Se pueden mostrar múltiples espectros en la ventana para compararlos o con el propósito de hacer una figura. Arrastre el cursor horizontal (en el mapa de calor, arriba a la izquierda) hasta el punto de tiempo deseado. Presione Ctrl + S para seleccionar el espectro y guardarlo en la ventana espectral (abajo a la izquierda). Agregue tantos puntos de tiempo como sea necesario para mostrar la progresión de los datos (5-10 espectros), como se ve en la Figura 3.
NOTA: El número de espectros elegidos para representar los datos y la disposición temporal de estos espectros pueden depender en gran medida de la muestra específica y de las condiciones experimentales. La recomendación anterior es una guía general, pero los detalles del experimento deben dictar qué partes del conjunto de datos se enfatizan. - Exporte como datos haciendo clic con el botón derecho en la ventana que contiene los espectros. Haga clic en la opción Exportar datos al portapapeles . Los datos se guardan temporalmente. Pegue estos datos en el documento de software deseado (es decir, Excel) y guárdelos.
- Se pueden mostrar varias trazas cinéticas en la ventana cinética de la misma manera que en la ventana de espectros. Arrastre el cursor vertical (en el mapa de calor, arriba a la izquierda) a la longitud de onda deseada. Presione Ctrl + X para seleccionar el seguimiento del tiempo y guardarlo en la ventana de cinética (arriba a la derecha). Agregue tantos puntos de tiempo como desee. Esto guardará temporalmente el trazado cinético actual en la ventana.
- Exporte como datos haciendo clic con el botón derecho en la ventana que contiene las trazas cinéticas. Haga clic en la opción Exportar datos al portapapeles . Los datos se guardan temporalmente. Pegue estos datos en el documento de software deseado (es decir, Excel) y guárdelos.
- Para exportar el mapa de calor del conjunto de datos, haga clic en el menú Archivo y, a continuación, haga clic en Exportar a CSV (Figura complementaria 15). Esto abrirá una ventana, haga clic en Aceptar para guardar el archivo csv en el mismo directorio que el archivo de datos abierto con el mismo nombre que el archivo de datos.
- Extracción de datos de un ajuste de longitud de onda única para su visualización
- Haga clic en el menú Cinética y, a continuación, haga clic en Ajustar cinética para abrir la ventana que contiene los datos ajustados.
- Haga clic con el botón derecho en la ventana de ajuste (es decir, el mosaico central en la ventana de ajuste único). Haga clic en Exportar datos al portapapeles. Esto lo guardará temporalmente para que pueda pegarse en un programa de software diferente.
NOTA: La gráfica residual debajo de los datos de ajuste no se puede exportar y, en su lugar, tendrá que volver a crearse a partir de los datos de ajuste. El ajuste exporta tanto los datos sin procesar como la línea de ajuste, que luego se puede utilizar para volver a crear el residuo. El residuo se crea restando el valor de ajuste de los datos en cada punto de tiempo y creando un gráfico similar al que se muestra en la ventana "Ajustar cinética". - Pegue estos datos en el documento de software deseado (es decir, Excel) y guárdelos.
NOTA: La exportación al portapapeles solo incluirá los datos sin procesar y los datos de la línea de ajuste para cada exponencial utilizada en el ajuste. Los parámetros del ajuste, como la vida útil, las amplitudes, etc., no se incluirán y tendrán que exportarse copiando los valores del software de ajuste.
- Extracción de datos del análisis global de la vida útil para su visualización y análisis
- Haga clic en el menú Superficie y, a continuación, haga clic en la opción Ajuste global para abrir la ventana que contiene los datos ajustados.
- La precisión de los valores de los ejes de densidad óptica y retardo de tiempo/longitud de onda deberá ajustarse para los componentes principales (mosaico superior derecho) y DADS (mosaico inferior izquierdo), respectivamente. Coloque el ratón sobre la ventana del componente principal hasta que aparezca el cuadro de configuración en la parte inferior derecha.
- Haga clic rápidamente en el botón x.xx , pase el mouse sobre "Precisión" y haga clic en 6 en el menú para establecer el número de decimales que se incluirán.
- Coloque el ratón sobre la ventana del componente principal hasta que aparezca el cuadro de configuración en la parte inferior derecha. Haga clic rápidamente en el botón y.yy , pase el ratón por encima de "Precisión" y haga clic en 6 en el menú para establecer el número de decimales que desea incluir.
- Haga clic con el botón derecho en la ventana Trazos cinéticos principales . Haga clic en Exportar datos al portapapeles. Esto lo guardará temporalmente para que pueda pegarse en un programa de software diferente.
- Pegue estos datos en el documento de software deseado (es decir, Excel) y guárdelos.
NOTA: Los datos se guardarán como una serie de columnas que contienen primero los retardos de tiempo, luego las trazas cinéticas principales seguidas de la línea de ajuste. Habrá un conjunto para cada componente principal seleccionado al prepararse para el análisis global. Los espectros DADS ya se han guardado como parte del procedimiento de ajuste en el paso 2.4.7.
Resultados
La preparación y análisis de una muestra de 1,4-Bis[2-(5-feniloxazolil)]benceno, POPOP en etanol se llevó a cabo siguiendo el procedimiento descrito anteriormente. Las mediciones se llevaron a cabo utilizando un espectrómetro de absorción transitoria ultrarrápida, como se describe en la Figura 1, con soluciones fluidas en cubetas de 2 mm utilizando un soporte de cubeta ajustable y un agitador magnético para garantizar la mezcla. Las muestras se midieron en condiciones ambientales sin controles adicionales de temperatura o atmósfera. La ventana óptica de 340 nm a 680 nm se generó utilizando un cristal de fluoruro de calcio. Se recolectaron doscientos cincuenta (250) puntos de tiempo entre -5 ps y ~5500 ps, y se promediaron tres escaneos para generar el conjunto de datos final, Figura 3. Los datos de POPOP se prepararon como se describe en el protocolo. En la Figura complementaria 16 se muestra un ejemplo de corrección de chirp subóptima. El ajuste cinético de una sola longitud de onda se realizó en POPOP, seleccionando 632 nm como longitud de onda de interés. Además, se llevó a cabo un análisis global de POPOP como se describe en el protocolo.
El ajuste cinético de una sola longitud de onda de POPOP a 632 nm produjo dos vidas útiles. Se permitió que estas vidas variaran y no se hicieron más ajustes. Los parámetros finales obtenidos fueron los siguientes: t0 = −0,1176 ps, IRF = 0,436 ps, A1 = 0,0956, t1 = 1,614 ps, A2 = 0,0646, t2 = 522,2 ps (Figura 4). Estos resultados concuerdan bien con el análisis global realizado posteriormente y los valores de vida útil de las emisiones notificados para los POPOP (τ = 1,35 ns)17. En la Figura complementaria 16 se muestra y analiza un ejemplo de ajuste de una sola longitud de onda con muy pocos componentes de vida útil.
El ajuste del análisis global en POPOP se realizó después de seleccionar 15 componentes principales (PC) al realizar SVD. Se seleccionaron dos tiempos de vida después del ajuste, no se fijaron parámetros. Los parámetros finales obtenidos del ajuste fueron los siguientes: t0 = −0,1586 ps, tp (IRF) = 0,4408 ps, t1 = 1459 ps, t2 = 267,5 ps. Los espectros de diferencia asociados a la desintegración se muestran en la Figura 5. Los resultados concuerdan bien con los del ajuste cinético único a 632 nm y los valores de vida útil para POPOP17. En la Figura complementaria 16 se muestran y analizan dos ejemplos de análisis global subóptimo.
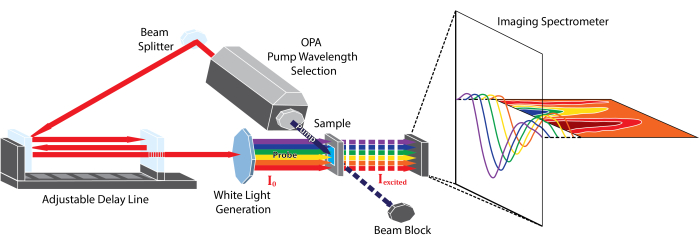
Figura 1: Representación esquemática del instrumento de absorción transitoria de banda ancha de femtosegundos descrito en este protocolo. Haga clic aquí para ver una versión más grande de esta figura.
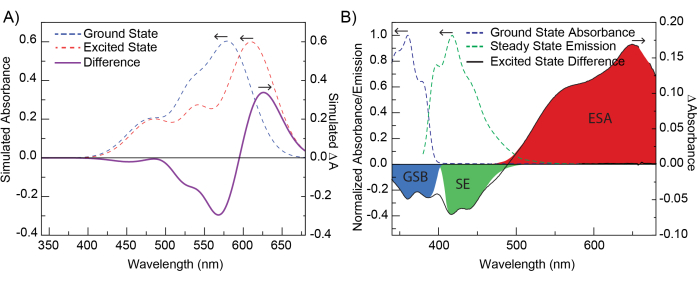
Figura 2: Simulación de los datos de TAS y contribuciones a la señal de TAS. (A) Curvas gaussianas que simulan un espectro de absorción en estado fundamental (línea punteada azul) y un espectro en estado excitado (línea punteada roja, desplazada al rojo desde el espectro en estado fundamental). Los espectros de diferencia de estos dos espectros (púrpura, línea continua) es el espectro de diferencia visto en TA. Las diferencias entre los espectros del estado fundamental y excitado se han exagerado con fines ilustrativos. (B) Un espectro representativo de diferencia de TA de POPOP a 1,04 ps después de la excitación a 330 nm. Las líneas punteadas muestran la absorbancia en estado fundamental y la emisión en estado estacionario de POPOP. Las regiones resaltadas muestran características comunes de AT, lejía en estado fundamental (GSB), emisión estimulada (SE) y absorbancia en estado excitado (ESA) observadas en estos datos. Haga clic aquí para ver una versión más grande de esta figura.
Figura 3: Datos preparados para POPOP que resultan de la aplicación del paso 1 - Preparación de datos. Los datos se muestran como el mapa de calor corregido y los espectros representativos. Estos resultados demuestran cómo deben verse los datos después de que se hayan aplicado las correcciones y se esté listo para aplicar un ajuste al conjunto de datos. Haga clic aquí para ver una versión más grande de esta figura.
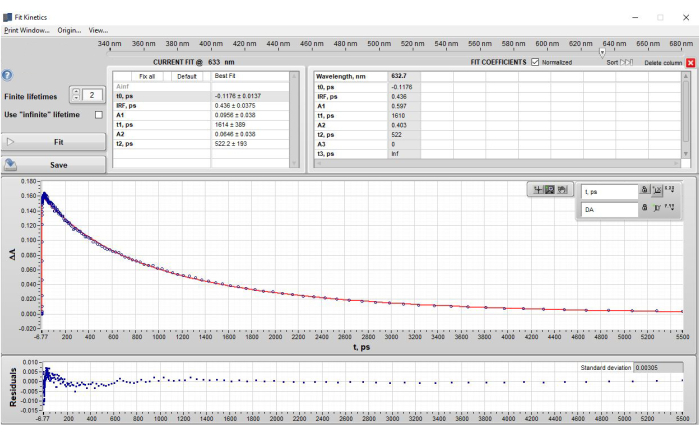
Figura 4: Resultados del ajuste de una sola longitud de onda de POPOP a 632 nm después de la aplicación del paso 2.3 - Ajuste de una sola longitud de onda. La figura muestra (sección superior) los tiempos de vida obtenidos en formato de tabla, (sección central) los datos (puntos azules) y el ajuste a los datos (línea de ajuste roja), y (sección inferior) el gráfico residual. Tenga en cuenta que en la sección "ajuste de corriente", las amplitudes (A) se muestran como los valores ΔA de los datos que representan la contribución de ese componente de vida útil específico en t0. Sin embargo, cuando el ajuste actual se guarda y aparece en la tabla "Coeficientes de ajuste", la configuración predeterminada es mostrar las amplitudes normalizadas. Esta configuración se puede cambiar desmarcando la casilla junto a la etiqueta "Coeficientes de ajuste" "Normalizado". Haga clic aquí para ver una versión más grande de esta figura.
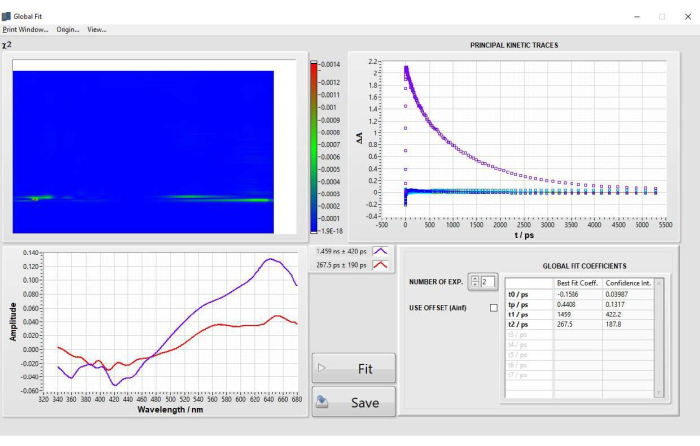
Figura 5: Resultados del ajuste del análisis global de POPOP obtenidos después del ajuste del paso 2.4. Haga clic aquí para ver una versión más grande de esta figura.
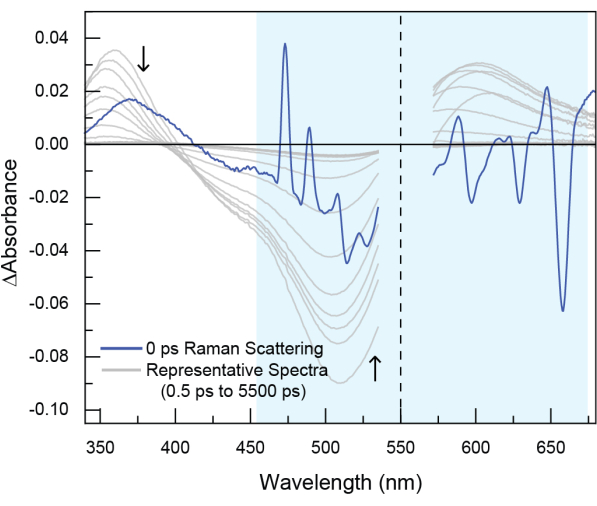
Figura 6: Ejemplo de dispersión Raman estimulada observada en datos experimentales de AT. En este conjunto de datos (no en los datos POPOP que se muestran en el tutorial), la muestra se excitó a 550 nm (indicado por la línea de puntos). La dispersión Raman se ve alrededor del tiempo cero y generalmente aparece tanto en el azul (dispersión Raman anti-Stokes) como en el rojo (dispersión Raman de Stokes) de la longitud de onda de excitación de la bomba. La dispersión Raman estimulada es de corta duración, normalmente sólo alrededor de ~200 fs, porque se produce como resultado de la interacción del haz de la sonda con la muestra al mismo tiempo que el haz de la bomba, estimulando así el proceso Raman. Sin embargo, la característica no se puede evitar y debe eliminarse con el recorte. Haga clic aquí para ver una versión más grande de esta figura.
Figura complementaria 1: Menú principal cuando se cargan los datos por primera vez. Generalmente, en este software de ajuste habrá cuadros de opciones que aparecerán en la esquina inferior derecha de una ventana cuando se pase el ratón sobre la ventana. Estos cuadros permiten modificar la interacción del cursor con la ventana, ya sea moviendo selecciones, haciendo zoom o encuadrando las ventanas seleccionadas. También hay opciones para ajustar la precisión de las escalas del eje x y del eje y para la ventana, así como para cambiar la visualización de lineal a logarítmica. Los ejes también se pueden bloquear o desbloquear. Mientras esté bloqueado, un eje permanecerá en el nivel de zoom o en el rango de valores especificados; Cuando se desbloquea, el rango cambiará para contener el conjunto completo de datos. Otras opciones permiten ajustar la visualización de los números y el color de las cuadrículas, si están presentes. Haga clic aquí para descargar este archivo.
Figura complementaria 2: Menú de superficie para realizar la sustracción de luz dispersa. Haga clic aquí para descargar este archivo.
Figura suplementaria 3: Restar la pantalla de luz dispersa: establecer los espectros en promedio. Haga clic aquí para descargar este archivo.
Figura complementaria 4: Ajuste del rango de recorte. Haga clic aquí para descargar este archivo.
Figura complementaria 5: Conjunto de datos de recorte. Los datos recortados se eliminarán de forma permanente. Haga clic aquí para descargar este archivo.
Figura complementaria 6: Ajuste de la ventana de respuesta al disolvente y ejemplo de ajuste de la respuesta al disolvente (en línea roja) a los datos (puntos azules). Haga clic aquí para descargar este archivo.
Figura complementaria 7: Ventana de corrección de chirridos con datos de muestra "en blanco". Haga clic aquí para descargar este archivo.
Figura 8 complementaria: Corrección del chirrido que se muestra junto con el conjunto de datos. Haga clic aquí para descargar este archivo.
Figura suplementaria 9: Ventana de ajuste cinético único. Además, un control deslizante en la parte superior permite al usuario seleccionar la longitud de onda en la que desea realizar el ajuste. La selección de una longitud de onda apropiada requiere el conocimiento de la espectroscopia del sistema para identificar dónde ocurren los procesos de interés. Algunos ejemplos son los productos de transferencia de carga, la formación de tripletes o la formación de fotoproductos, cuyas características espectrales se sabe que se correlacionan con longitudes de onda específicas. Estas longitudes de onda específicas se pueden ajustar para obtener la vida útil de esos eventos específicos. Además, se puede utilizar una selección de longitudes de onda para proporcionar validación a un modelo de ajuste global seleccionado. Haga clic aquí para descargar este archivo.
Figura complementaria 10: Configuración de los parámetros de ajuste cinético único. Los parámetros de ajuste individuales se pueden fijar o modificar a mano si se desea para ajustar el ajuste y minimizar la desviación estándar del residuo. Nota: Los parámetros se pueden ajustar fácilmente haciendo clic en el valor en el cuadro y luego ajustándolos con un control deslizante o escribiendo manualmente un valor. El ajuste mostrado se ajustará en tiempo real a medida que se cambien los valores. Cuando se logra un ajuste aceptable, el ajuste se puede exportar haciendo clic con el botón derecho en la pantalla de ajuste, lo que permite exportar los datos al portapapeles para pegarlos en el programa deseado o como una imagen para una visualización rápida. Haga clic aquí para descargar este archivo.
Figura complementaria 11: Se pueden restringir y fijar los valores de los parámetros de ajuste cinético único si uno o más parámetros son bien conocidos. Haga clic aquí para descargar este archivo.
Figura complementaria 12: Ventana de descomposición de valor único con componentes principales que muestra cómo se verán el seguimiento y los componentes cuando se agreguen suficientes componentes principales. Haga clic aquí para descargar este archivo.
Figura complementaria 13: Ventana de ajuste global antes de que se genere el ajuste del análisis global. Haga clic aquí para descargar este archivo.
Figura complementaria 14: Ventana de ajuste global que muestra los resultados del ajuste del análisis global. Haga clic aquí para descargar este archivo.
Figura complementaria 15: Menú de archivos para guardar y exportar archivos. Haga clic aquí para descargar este archivo.
Figura complementaria 16: Ejemplos de corrección y ajuste de chirp subóptimos. (A) demuestra un ajuste cinético simple deficiente. El tipo de residuo estructurado que se muestra en el panel A suele indicar que se requiere una vida útil adicional para ajustar los datos. Observe que el residuo cae por debajo de cero en tiempos más cortos y se eleva por encima de la línea cero en vidas más largas. (B) muestra una corrección correcta del chirrido utilizando el botón de vista previa, en el que las entidades se enderezan y no hay curvatura presente en los datos. (C) demuestra una corrección incorrecta del chirrido en la que hay una curvatura notable presente en la parte azul del espectro, lo que indica que la función del chirrido está sobrecorrigiendo en esta región. (D) muestra un ajuste deficiente del análisis de la vida útil global en el que el sobreajuste (incluidos demasiados parámetros) ha dado como resultado DADS "simétricos" (que parecen imágenes especulares entre sí a lo largo del eje x) de rangos de vida útil similares que esencialmente se cancelan entre sí. Cuando se observan estas características, no se debe utilizar el ajuste. (E) muestra un ajuste global deficiente en el que demasiados parámetros han dado lugar a una vida útil muy corta con una amplitud muy grande. El problema presente en (E) también puede aparecer si los artefactos alrededor del tiempo cero no se corrigen correctamente y el ajuste se centra en minimizar el residuo al enfatizar demasiado la vida útil muy corta (una que no es físicamente significativa). Haga clic aquí para descargar este archivo.
Figura complementaria 17: Ejemplo de datos TAS con dispersión Raman. La dispersión está presente alrededor del tiempo cero y coincide con la longitud de onda de excitación de la bomba. La dispersión consiste en una serie de picos agudos con un pico azul positivo muy intenso de la excitación de la bomba y un pico rojo negativo de la excitación de la bomba. Esta característica no se puede evitar razonablemente y debe eliminarse de los datos para evitar interferir con los resultados de ajuste. Haga clic aquí para descargar este archivo.
Archivo complementario 1: Archivo que contiene el conjunto de datos de este tutorial (POPOP data_POPOP-inEtOH.ufs). Haga clic aquí para descargar este archivo.
Archivo complementario 2: Archivo que contiene un conjunto de datos en blanco para este tutorial (POPOP data_BLANK.ufs). Haga clic aquí para descargar este archivo.
Archivo complementario 3: Archivos de información de apoyo que contienen comentarios adicionales sobre el ajuste de la respuesta al solvente, la corrección del scatting y la sustracción de superficies. Haga clic aquí para descargar este archivo.
Discusión
Consideraciones generales para la preparación de datos
El ajuste de los datos de AT puede parecer a primera vista relativamente sencillo, y podría esperarse que se produzca una "respuesta" correcta y clara para un conjunto de datos determinado. Sin embargo, como se destaca en el protocolo, hay muchos factores en la adquisición, preparación y análisis de datos que se deben considerar cuidadosamente y que pueden generar incertidumbre sobre qué modelo o conjunto de parámetros de ajuste describe mejor los datos. El objetivo de la preparación y el ajuste de los datos es reducir la mayor cantidad posible de estos factores extraños, al tiempo que se preservan los datos para su análisis. La tarea en cuestión puede parecer desalentadora para un principiante, ya que hay mucho que considerar. Para desarrollar la intuición sobre el proceso de ajuste, se anima al principiante a intentar preparar los mismos datos varias veces desde cero de formas ligeramente diferentes para comprobar cómo afectan drásticamente los pasos de preparación de datos al mejor ajuste. Además, dos investigadores diferentes pueden preparar y ajustar los mismos datos y comparar los resultados. Este proceso puede llevar mucho tiempo las primeras veces, sin embargo, hacerlo permitirá al principiante desarrollar la intuición sobre cómo preparar los datos de forma coherente para futuras muestras. Como cualquier habilidad, esta preparación y ajuste de datos tomará tiempo para desarrollarse, y se recomienda al principiante que sea paciente y disciplinado al experimentar y aprender el proceso. El conjunto de datos utilizado en este estudio se proporciona para dar al principiante la oportunidad de encajar directamente con el tutorial y comparar directamente los resultados con los producidos en el tutorial.
Los datos pueden contener características de fondo que están presentes en todos los retardos de tiempo (Figura complementaria 2 y Figura complementaria 3), como la dispersión del haz de la bomba y la emisión espontánea de la muestra. Estas características no deseadas deben eliminarse para aislar la señal de absorción transitoria de la especie de interés11. La eliminación de estas características se realiza eligiendo, promediando y eliminando la contribución de una serie de espectros de diferencia de tiempo negativos. Al seleccionar los espectros de fondo, es importante asegurarse de que no se incluya ninguna entidad que pueda formar parte del proceso de interés para su eliminación. Las características de fondo que surgen del disolvente, como la absorción de impurezas o del propio disolvente, también pueden observarse en los datos de AT. Cuando el disolvente produce una señal, será necesario restar del conjunto de datos de la muestra un conjunto de datos "en blanco" que contenga solo el disolvente en las mismas condiciones experimentales exactas que la muestra. Los detalles sobre este procedimiento se incluyen en el Expediente Complementario 3.
La corrección del chirrido es otro factor a considerar cuidadosamente. El chirrido se produce a medida que el pulso de la sonda viaja a la muestra y se ensancha debido a imperfecciones en los espejos de dirección o al pasar a través de ópticas dispersivas como lentes o filtros. El resultado final es que los fotones de menor energía en el pulso de la sonda (es decir, el lado rojo del espectro de la sonda) llegan a la muestra antes que los fotones de mayor energía (es decir, el lado azul del espectro de la sonda). Esto da como resultado que el "tiempo cero" de los espectros de TA se difumine durante varios femtosegundos o picosegundos18, lo que se manifiesta como una curva distinta en el conjunto de datos sin procesar que comienza en las longitudes de onda azules y luego se aplana a medida que se acerca al rojo (Figura suplementaria 7). El chirrido es más notable en escalas de tiempo más cortas, como las que se obtienen mediante TA ultrarrápida. Este tiempo cero dependiente de la longitud de onda se puede corregir como se describe en el protocolo, pero la aplicación de este proceso puede ser complicada y subjetiva. Tener una muestra "en blanco" o una medición de la respuesta de Kerr del solvente puede minimizar la naturaleza subjetiva de los puntos de selección manual para la corrección del chirp necesaria para generar el ajuste polinómico utilizado para ajustar y corregir el chirrido. El objetivo de la corrección del chirrido es eliminar la "curva" distintiva del tiempo cero. Es posible que se necesiten varios intentos de ajuste del chirrido para obtener los mejores datos corregidos por el chirrido. Los datos se pueden ajustar varias veces con diferentes correcciones de chirp aplicadas para comprender el impacto que tiene la corrección de chirp en los valores de las cortas vidas de TA.
Artefactos que aparecen en el "tiempo cero"
Se pueden observar varios artefactos cerca del "tiempo cero" en los datos de TA, incluida la dispersión de Rayleigh, la dispersión Raman estimulada y la modulación de fase cruzada. La dispersión de Rayleigh del haz de la bomba es una dispersión elástica que da como resultado un cambio en la energía. Esta función aparecerá en la misma longitud de onda que el pulso de la bomba. La dispersión Raman estimulada puede acompañar a la señal de dispersión de la bomba19. La dispersión Raman, que resulta de la dispersión inelástica de un fotón de bombeo, produce picos tanto de energía más alta (anti-Stokes) como más baja (Stokes) que la energía de la bomba incidente. En los datos de TA, se observa una dispersión Raman estimulada debido a la irradiación simultánea de la muestra con los haces de la bomba y la sonda. Cuando el haz de la sonda interactúa con la muestra al mismo tiempo que el haz de la bomba, estimula el proceso Raman. Por lo tanto, la dispersión Raman estimulada ocurre alrededor del tiempo cero y da como resultado picos adicionales en los espectros dentro de los primeros cientos de femtosegundos (Figura 6, observada en el espectro azul más oscuro en la región resaltada y Figura suplementaria 17). La modulación de fase cruzada se origina a partir de la modulación del índice de refracción del disolvente a partir de la interacción con el intenso campo eléctrico de un pulso.
La dispersión Raman estimulada puede distinguirse de la modulación de fase cruzada porque los picos Raman aparecen a frecuencias específicas que corresponden a los modos vibratorios del disolvente. Debido a que es un proceso Raman, se pueden observar tanto las líneas de Stokes como las anti-Stokes a ambos lados de la excitación. Los disolventes clorados como el cloruro de metileno muestran bandas Raman muy prominentes debido a la gran polarizabilidad del cloro. Las firmas espectrales de la modulación de fase cruzada son exclusivas de un disolvente, pero no son tan fáciles de predecir como las características de dispersión Raman.
Dependiendo de la cinética de la muestra que se está midiendo, la dispersión de Rayleigh, la dispersión Raman y la modulación de fase cruzada pueden superponerse con las características iniciales de los datos de TA y pueden ser difíciles de eliminar de los datos. En principio, estas características se pueden ver en una medición ordenada del disolvente y se restan de los datos, los programas de análisis de datos pueden tener funciones adecuadas para tener en cuenta estas características, pero en la práctica, esto puede ser difícil. Cuando es demasiado difícil sustraer estos artefactos sin comprometer los datos de muestra, puede ser mejor recortar los espectros comprometidos alrededor del tiempo cero para eliminar los artefactos. Si lo hace, tendrá el desafortunado efecto secundario de eliminar los primeros aproximadamente 300 fs de datos, pero hará que el ajuste sea más confiable más adelante. En el transcurso del análisis de múltiples conjuntos de datos de la misma y diferentes muestras, el principiante ganará intuición para lograr este equilibrio de restar la superficie de fondo frente a recortar los datos iniciales de 100-200 fs.
Puede ser necesario un recorte general para las partes de los espectros que contienen una relación señal-ruido baja. La inestabilidad en el haz de la sonda en ciertas regiones, la baja intensidad de la luz de la sonda, las concentraciones de muestra que son demasiado altas (bloqueando así gran parte de la sonda incidente), la baja intensidad de la bomba y la sección transversal de absorción de la muestra son culpables típicos de la baja relación señal-ruido que puede dificultar el ajuste de los datos. En estos casos, recortar el conjunto de datos a ambos lados de la ventana óptica para lograr el nivel deseado de relación señal-ruido puede ayudar al proceso de ajuste.
Un conjunto de datos está listo para el análisis una vez que se ha recortado lo suficiente como para eliminar las secciones deficientes del conjunto de datos, se ha corregido el chirrido y se han promediado y restado los espectros de fondo. Este procedimiento debe dar lugar a datos que contengan sólo las partes más relevantes para la fotofísica y la fotoquímica de interés. De hecho, está claro que hay cierto grado de subjetividad en este proceso. El objetivo en la preparación de datos es lograr un equilibrio entre la eliminación de artefactos para que no perturben el ajuste, pero no la eliminación tanto como para comprometer la integridad del conjunto de datos, lo que dificulta su interpretación. Encontrar este equilibrio requiere tiempo y experiencia para desarrollar la intuición de lo que es un artefacto y lo que son datos. Ajustar (y volver a ajustar) el mismo conjunto de datos en varios días diferentes, o hacer que dos investigadores ajusten los mismos datos, puede ser una forma de minimizar el error humano y la subjetividad de la preparación y el análisis de los datos.
Consideraciones generales para el ajuste y la interpretación
Una vez procesados los espectros de AT en bruto, deben interpretarse y modelarse para extraer información sobre las especies y la dinámica presente en el sistema de interés. Este proceso puede describirse como un procedimiento de tres pasos que incluye la interpretación espectral inicial, el modelado/ajuste cuantitativo y la asignación de la interpretación espectral al modelo/ajuste.
Interpretación espectral inicial: En la etapa de interpretación espectral, el objetivo es asignar las características presentes en los espectros de AT a los estados electrónicos a los que se accede en la evolución fotofísica o fotoquímica del sistema. Para empezar, hay que identificar varios estados. En este trabajo, los estados se refieren a estados electrónicos únicos que forman parte de la evolución fotofísica o fotoquímica del sistema. Un estado, representado, por ejemplo, por una curva de energía potencial específica (PEC), posee un conjunto de picos característicos que representan su espectro de absorción. Un cambio que se produce dentro de un solo estado se denomina proceso. Un proceso fotofísico puede aparecer en los espectros de AT como un desplazamiento de pico o un cambio en el ancho del espectro. El aspecto clave de un proceso es que la población del estado permanezca igual (es decir, que el proceso ocurra dentro de un PEC determinado); Lo que cambia es la distribución de la energía dentro del Estado. Un cambio en la población de un estado se denominará transición. Durante una transición, el sistema evoluciona a otro PEC (es decir, estado electrónico). Las transiciones pueden incluir la conversión interna (IC), el cruce entre sistemas (ISC), la transferencia de carga, la transferencia de energía, la formación de nuevos productos o el retorno al estado fundamental. En los párrafos siguientes se describen las directrices para asignar estados, procesos y transiciones.
Asignación de estados
El primer paso en este proceso consiste en asignar características espectrales a especies o estados químicos específicos. El estado S1 en TA debe mostrar un tiempo de vida que coincida con el tiempo de vida de fluorescencia tomado mediante espectroscopia de emisión resuelta en el tiempo. Un estado triplete puede ser verificado si su vida útil es apagada por el oxígeno. Si se sospecha la existencia de un anión o catión radical en la evolución fotofísica, se puede realizar espectroelectroquímica u oxidación/reducción química para generar las especies radicales, y se puede obtener un espectro de absorción de esa especie y compararlo con la forma de banda de TA. Se puede realizar una espectroscopia de resonancia de espín electrónico (ESR) para verificar la presencia de radicales libres. Una excelente charla tutorial organizada por la División de Química Inorgánica de la ACS ofrece una visión general de la AT y de las consideraciones que se tienen en cuenta en la asignación de características20. Una vez que las bandas han sido asignadas a las especies, el siguiente paso en la interpretación de los espectros de AT es describir cualitativamente los procesos dinámicos que ocurren en el sistema. Este paso es vital, ya que le da al investigador una idea de qué modelos serán apropiados para describir su sistema y le dará una línea de base para comparar los parámetros de ajuste.
Cambios dentro de un estado
El enfriamiento vibracional, el reordenamiento geométrico o la solvatación son procesos extremadamente rápidos (sub-ps a 10's ps) que se pueden observar con TA. El enfriamiento vibracional se observa como un rápido desplazamiento hacia el azul del espectro TA en una escala de tiempo de varios picosegundos 21,22,23. El reordenamiento geométrico puede ocurrir en la escala de tiempo ps de 10. La dinámica de solvatación se observa como un corrimiento al rojo y un estrechamiento del espectro durante varios picosegundos en líquidos dipolares convencionales, pero los disolventes de alta viscosidad como el glicerol, el polietilenglicol (PEG), los líquidos iónicos y los disolventes eutécticos profundos pueden exhibir una dinámica de solvatación que se produce en el transcurso de varios nanosegundos 24,25,26.
Cambios en la población de un estado
Las reacciones se caracterizan por un cambio en la intensidad de una banda, donde una disminución en la intensidad se asocia con una disminución en la concentración de sus especies químicas y viceversa para un aumento. En algunos casos, tanto las especies reactivas como las del producto son visibles en los espectros, mientras que en otros, los estados del producto son demasiado efímeros o están demasiado desplazados al rojo para ser observados. A menudo, las transiciones de estado a estado se pueden observar por la presencia de un punto isostólico en los espectros.
Modelado cuantitativo/Ajuste: Un modelo debe ajustarse a los datos para extraer información cuantitativa sobre la dinámica del sistema. Como se describió anteriormente en la introducción, hay una amplia gama de modelos para usar. Este protocolo se centra en dos de los métodos más comunes: el ajuste de una sola longitud de onda y el análisis global. El método de una sola longitud de onda implica ajustar las trazas de longitud de onda individuales de los espectros a alguna forma funcional, típicamente una suma de exponenciales:
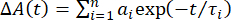 (2)
(2)
donde ΔA(t) es la señal TA en una longitud de onda elegida, n es el número de componentes exponenciales, y aies la amplitud del componente exponencial, i, con la constante de tiempo τi. Se pueden agregar varios componentes hasta que el ajuste reproduzca los datos experimentales. El objetivo de cualquier proceso de ajuste es modelar los datos utilizando suficientes tiempos de vida para reproducir bien los datos, pero no sobreajustar los datos al incluir demasiados componentes. Por lo tanto, los parámetros ponderados de bondad de ajuste, como 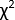 , se utilizan para ayudar a determinar cuándo los datos se ajustan a las incertidumbres experimentales5.
, se utilizan para ayudar a determinar cuándo los datos se ajustan a las incertidumbres experimentales5.
Una vez que el decaimiento se ajusta satisfactoriamente, los parámetros del modelo se pueden utilizar para caracterizar la dinámica del sistema. A continuación, se pueden extraer e interpretar las constantes de tiempo resultantes. Desafortunadamente, el gran número de características superpuestas en los espectros de TA significa que una sola longitud de onda en el espectro puede contener dinámicas correspondientes a diferentes especies cuyas firmas espectrales se superponen, lo que significa que las constantes de tiempo extraídas de un ajuste de una sola longitud de onda pueden representar una combinación de múltiples procesos coincidentes. Además, cualquier cambio en la forma y posición de la banda también influirá en las amplitudes y las constantes de tiempo extraídas del ajuste de una sola longitud de onda. Estos problemas pueden evitarse en algunos casos mediante un método adecuado llamado "análisis de la forma de la banda", en el que se determina o se asume una forma funcional para las bandas de TA de cada especie absorbente del sistema. Estas formas se ponderan por amplitudes dependientes del tiempo y se suman para reproducir el espectro observado. Este procedimiento se usa comúnmente en el análisis de espectros de fluorescencia resueltos en el tiempo, pero las formas más complicadas y los componentes superpuestos de las bandas de TA hacen que este método sea sostenible solo en unos pocos casos simples, como se detalla en otra parte10.
Otro inconveniente del ajuste de una sola longitud de onda es que no aprovecha intrínsecamente el amplio rango espectral que ofrecen los experimentos modernos de AT. Se podría, en principio, ajustar metódicamente cada longitud de onda individual de los espectros, pero dicho análisis es engorroso, requiere mucho tiempo y es computacionalmente costoso. Para combatir este desafío, se puede utilizar un método llamado "análisis global" para ajustar simultáneamente un conjunto completo de espectros de AT a un conjunto de parámetros dinámicos compartidos4. El análisis global, y un método estrechamente relacionado llamado análisis de objetivos, son métodos exitosos y ampliamente utilizados, pero también vienen con su propio conjunto único de inconvenientes y limitaciones. Al igual que con cualquier modelo, es imperativo comprender los supuestos que se utilizan para crearlo, así como las limitaciones que presentan.
En el análisis global, los espectros de TA están representados por una matriz m por n, donde m representa el número de longitudes de onda medidas en cada espectro y n representa el número de puntos de tiempo recogidos. Se supone entonces que esta matriz es descomponible en el producto de otras dos matrices:
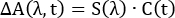 (3)
(3)
donde C(t) es una matriz de n por k y S(λ) es una matriz de m por k. El valor k representa el número de componentes espectrales distintos utilizados para reproducir los espectros. Cada uno de estos componentes representa una especie absorbente con una firma espectral y una dinámica únicas. La matriz S(λ) representa los espectros TA de los k componentes y C(t) sus concentraciones dependientes del tiempo. En la implementación más simple y común del análisis global, se supone que cada componente tiene una cinética exponencial simple (i = 1 en la Ecuación 2, con cada componente asignado a su propia constante de tiempo). En resumen, el espectro completo de TA se puede representar mediante la suma de k componentes de espectros, cada uno con su propio espectro de absorción característico y decaimiento exponencial único.
Cuando los espectros TA están ajustados, el usuario adivina cuántos componentes (es decir, un valor para k) se necesitan y hace una conjetura sobre la constante de tiempo asociada con una desintegración exponencial simple de esas especies. A continuación, el ajustador genera Cguess(t) y resuelve la ecuación 3 para Sfit(t). A continuación, Sfit(λ) y Cguess(t) se multiplican como en la Ecuación 3 para crear los espectros ajustados, ΔA(λ,t)fit. Finalmente, los residuos, ΔA(λ,t)exp − A(λ,t)fit, se minimizan y se devuelven las constantes de tiempo y Sfit(λ) y de tiempo óptimas. La relativa simplicidad del análisis global, que representa un conjunto completo de espectros utilizando un puñado de constantes de tiempo y componentes espectrales fijos, lo convierte en un método atractivo (y exitoso) para desenredar las complicadas formas de banda y la dinámica que se encuentran en la espectroscopia de TA. Sin embargo, se debe tener cuidado para garantizar que el análisis global sea un modelo apropiado para el sistema en cuestión.
Una suposición clave en el análisis global, ilustrada en la Ecuación 3, es la separabilidad completa de las porciones de longitud de onda y tiempo de la dinámica, una propiedad llamada "bilinealidad". Esta suposición requiere que las formas de banda de los componentes sean independientes del tiempo (es decir, que tengan una forma espectral fija que no varíe ni se desplace con el tiempo). Lo único que cambia durante el experimento son las poblaciones relativas de cada componente, representadas por C(t). En escalas de tiempo largas, ~ 1 ns más o menos, esta suposición generalmente se mantiene y el análisis global se puede usar sin mucha preocupación. Por otro lado, los procesos de estado excitado, como el enfriamiento vibracional y la dinámica de solvatación, prominentes en las escalas de tiempo ultrarrápidas accesibles por TA de femtosegundos, dan como resultado cambios dependientes del tiempo en la firma espectral de una especie y una ruptura de la bilinealidad. Esto no significa que el análisis global no pueda reproducir un conjunto de datos, de hecho, siempre puede producir un ajuste satisfactorio siempre que se utilice un número suficiente de componentes. El problema radica entonces en interpretar los espectros de los componentes y asignar las constantes de tiempo a procesos particulares de estado excitado, ya que los componentes pueden ya no corresponder a distintas especies absorbentes. Por lo tanto, siempre se debe tener cuidado al aplicar el análisis global a situaciones en las que no se puede asumir la bilinealidad.
Asignación de la interpretación espectral al modelo/ajuste: Una vez que se obtiene un ajuste, la interpretación espectral debe asignarse a los tiempos de vida obtenidos en el ajuste. Los tiempos de vida del ajuste se asignan tanto a los procesos como a las reacciones que se identificaron en la interpretación inicial de los espectros. Sin embargo, es posible que la evaluación inicial a partir de los espectros y el número de tiempos de vida ajustados obtenidos por el modelo no se correspondan inmediatamente entre sí. En esta situación (¡común!), el instalador debe volver atrás y evaluar la interpretación inicial. Tal vez hubo un enfriamiento vibratorio u otro proceso que se pasó por alto en la evaluación inicial, pero que se identificó en el proceso de modelado y ajuste. O bien, tal vez dos conjuntos diferentes de parámetros de ajuste podrían reproducir bien los datos y la interpretación inicial podría guiar qué conjunto de parámetros de ajuste se eligen. En este paso final, el instalador debe ir y venir entre la interpretación y el ajuste para encontrar una descripción que conduzca a una asignación fotofísica plausible de las especies y la dinámica del sistema. También se pueden explorar otros programas de ajuste que incluyen modelos de ajuste secuenciales, como el análisis de objetivos, para complementar los ajustes producidos por el análisis global y el software de ajuste presentado en este artículo4.
En resumen, este protocolo analiza la preparación y el ajuste de los datos de absorción transitoria. Su objetivo es poner de relieve los desafíos asociados con el proceso y comentar las formas de evitarlos o mitigarlos de manera práctica. Ajustar los datos de AT, como ajustar la mayoría de los datos que se encuentran en los campos técnicos, puede ser complicado y, a veces, subjetivo. Por lo tanto, es fundamental conocer el proceso y las limitaciones de los datos, la preparación de los datos y las herramientas matemáticas utilizadas para modelar y asignar significado a los datos. Los científicos deben abordar los datos y los modelos con un ojo crítico.
Uno puede intentar mitigar la subjetividad de sus ajustes. Por ejemplo, los datos se pueden preparar y ajustar desde diferentes puntos de partida y en diferentes días para garantizar que se produzca el mismo ajuste. Se pueden comparar los datos tomados en diferentes días con diferentes preparaciones de muestras. Varios investigadores pueden ajustar los mismos datos y comparar sus resultados. Con el tiempo, los investigadores pueden construir una intuición sobre los datos que obtienen (en función de los detalles de su configuración experimental y los parámetros experimentales) que les permitirá tener más confianza en sus ajustes.
Hay mucho que aprender sobre el ajuste de datos de TA y los detalles de los modelos discutidos en este artículo. Se recomiendan con entusiasmo varios artículos de revisión excelentes que profundicen en este tema 4,10,27. Este protocolo está destinado a ser una entrada para principiantes en el proceso de análisis y ajuste que estimule el interés en comprender más profundamente el proceso.
Divulgaciones
Los autores no tienen nada que revelar.
Agradecimientos
Este trabajo fue posible gracias al programa de Instrumentación de Investigación Principal de la NSF que estableció la instalación láser multiusuario para la absorción transitoria (CHE-1428633). Este material se basa en el trabajo apoyado por la Fundación Nacional de Ciencias bajo la Subvención No. CHE-2313290.
Materiales
| Name | Company | Catalog Number | Comments |
| EtOH 200% Proof | Decon Laboratories Inc | CAS 64-17-5 | Solvent used to prepare Sample |
| Helios transient absorption spectrometer | Ultrafast systems | https://ultrafast.systems/products/spectrometers-accessories/helios/ | Transient absorption spectrometer |
| POPOP 1,4-Bis[2-(5-phenyloxazolyl)]benzene | Tokyo Chemical Industry | CAS 1806-34-4 | Sample used for Examples |
| Surface Xplorer | Ultrafast systems | https://ultrafast.systems/products/spectrometers-accessories/surface-xplorer/ | Fitting program |
Referencias
- Turro, N. J. Modern Molecular Photochemistry. , University Science Books. (1991).
- Berera, R., van Grondelle, R., Kennis, J. T. M. Ultrafast transient absorption spectroscopy: Principles and application to photosynthetic systems. Photosynth Res. 101, 105-118 (2009).
- Ruckebusch, C., Sliwa, M., Pernot, P., de Juan, A., Tauler, R. Comprehensive data analysis of femtosecond transient absorption spectra: A review. J Photochem Photobiol C Photochem Rev. 13 (1), 1-27 (2012).
- Van Stokkum, I. H. M., Larsen, D. S., Van Grondelle, R. Global and target analysis of time-resolved spectra. Biochim Biophys Acta - Bioenerg. 1657 (2-3), 82-104 (2004).
- Megerle, U., Pugliesi, I., Schriever, C., Sailer, C. F., Riedle, E. Sub-50 fs broadband absorption spectroscopy with tunable excitation: putting the analysis of ultrafast molecular dynamics on solid ground. Appl Phys B Lasers Opt. 96 (2-3), 215-231 (2009).
- Kovalenko, S. A., Dobryakov, A. L., Ruthmann, J., Ernsting, N. P. Femtosecond spectroscopy of condensed phases with chirped supercontinuum probing. Phys Rev A - At Mol Opt Phys. 59 (3), 2369-2384 (1999).
- Villa, A., et al. Broadly tunable mid-infrared femtosecond pulses directly generated by an optical parametric amplifier. OSA Contin. 4 (11), 2837-2844 (2021).
- Brodeur, A., Chin, S. L. Ultrafast white-light continuum generation and self-focusing in transparent condensed media. J Opt Soc Am B. 16 (4), 637650(1999).
- Lang, B. Photometrics of ultrafast and fast broadband electronic transient absorption spectroscopy: State of the art. Rev Sci Instrum. 89 (9), 093112(2018).
- Beckwith, J. S., Rumble, C. A., Vauthey, E. Data analysis in transient electronic spectroscopy - an experimentalist's. Int Rev Phys Chem. 39 (2), 135-216 (2020).
- Devos, O., Mouton, N., Sliwa, M., Ruckebusch, C. Baseline correction methods to deal with artifacts in femtosecond transient absorption spectroscopy. Anal Chim Acta. 705 (1-2), 64-71 (2011).
- Surface Xplorer from Ultrafastsystems. , Available from: https://ultrafast.systems/products/spectrometers-a (2023).
- Gampp, H., Maeder, M., Meyer, C. J., Zuberbuhler, A. D. Calculation of equilibrium constants from multiwavelngth spectroscopic data-i mathematical considerations. Talanta. 32 (2), 95-101 (1985).
- Snellenburg, J. J., Laptenok, S., Seger, R., Mullen, K. M., van Stokkum, I. H. M. Glotaran: A Java-based graphical user interface for the R package TIMP. J Stat Softw. 49 (3), 1-22 (2012).
- Python scripts to convert to and from comma separated values (.csv) and Ultrafast Systems binary data (.ufs) file formats. , Available from: https://bitbucket.org/ptapping/csv2ufs/src/master/ (2023).
- Surface Xplorer manual. , Available from: https://ultrafastsystems.com/download/surface-xplorer/SurfaceXplorerManual.pdf (2023).
- Lakowicz, J. R. Principles of fluorescence spectroscopy, 3rd Ed. , Springer Science+Business Media, LLC. 883-886 (2006).
- Maciejewski, A., et al. Transient absorption experimental set-up with femtosecond time resolution. Femto- and picosecond study of DCM molecule in cyclohexane and methanol solution. J Mol Struct. 555 (1-3), 1-13 (2000).
- Lorenc, M., et al. Artifacts in femtosecond transient absorption spectroscopy. Appl. Phys. B Lasers Opt. 74, 19-27 (2002).
- Turro, C. Transient absorption spectroscopy. , Available from: https://mediaspace.unm.edu/media/Physical+Inorganic+Tutorials+Transient+Absorption+Specctrscopy/1_t5pdqzgx (2023).
- Maçôas, E. M. S., Mustalahti, S., Myllyperkiö, P., Kunttu, H., Pettersson, M. Role of vibrational dynamics in electronic relaxation of Cr(acac)3. J Phys Chem A. 119 (11), 2727-2734 (2015).
- Brown, A. M., et al. Vibrational relaxation and redistribution dynamics in Ruthenium(II) polypyridyl-based charge-transfer excited states: a combined ultrafast electronic and infrared absorption study. J Phys Chem A. 122 (40), 7941-7953 (2018).
- Vlček, A., Kvapilová, H., Towrie, M., Záliš, S. Electron-transfer acceleration investigated by time resolved infrared spectroscopy. Acc Chem Res. 48 (3), 868-876 (2015).
- Horng, M. L., Gardecki, J. A., Papazyan, A., Maroncelli, M. Subpicosecond measurements of polar solvation dynamics: Coumarin 153 revisited. J. Phys. Chem. 99 (48), 17311-17337 (1995).
- LaRocca, M. M., Baker, G. A., Heitz, M. P. Assessing rotation and solvation dynamics in ethaline deep eutectic solvent and its solutions with methanol. J Chem Phys. 155 (3), 034505(2021).
- Zhang, X. X., Liang, M., Ernsting, N. P., Maroncelli, M. Complete solvation response of coumarin 153 in ionic liquids. J Phys Chem B. 117 (16), 4291-4304 (2013).
- Jollife, I. T., Cadima, J. Principal component analysis: A review and recent developments. Philos Trans R Soc. A. 374 (2065), 20150202(2016).
Reimpresiones y Permisos
Solicitar permiso para reutilizar el texto o las figuras de este JoVE artículos
Solicitar permisoThis article has been published
Video Coming Soon
ACERCA DE JoVE
Copyright © 2025 MyJoVE Corporation. Todos los derechos reservados