10.10 : Moment of Inertia of Compound Objects
The moment of inertia is a quantitative measure of the rotational inertia of an object. It is defined as the sum of the products obtained by multiplying the mass of each particle of matter in a given body by the square of its distance from the axis. The total moment of inertia for compound objects can be found by determining and adding the moment of inertia of individual components together.
Consider a child of mass (mc) 25 kg standing at a distance (rc) of 1 m from the axis of a rotating merry-go-round. The merry-go-round is approximated as a uniform solid disk with a mass (mm) of 500 kg and a radius (rm) of 2 m. Find the moment of inertia of the compound system.
The total moment of inertia of the system can be determined by adding up the individual moments of inertia of the merry-go-round and the child rotating on the axis. Since the mass and size of the child are much smaller than the merry-go-round, the child can be considered as a point mass.
- The moment of inertia (I) for the child is calculated as
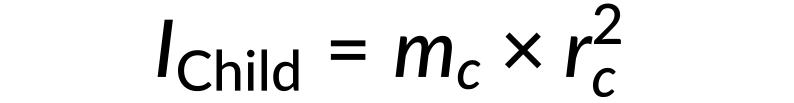
- The moment of inertia (I) for the merry-go-round is calculated as
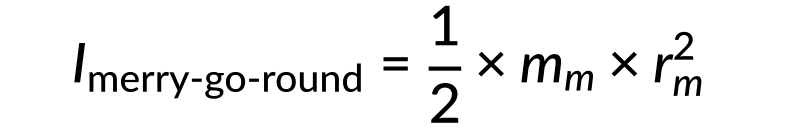
- By substituting and adding both values, the total moment of inertia of the system is determined to be 1025 kg⋅m2.
This text is adapted from Openstax, University Physics Volume 1, Section 10.5: Calculating Moments of Inertia.
Du chapitre 10:

Now Playing
10.10 : Moment of Inertia of Compound Objects
Rotation et systèmes matériels
6.1K Vues

10.1 : Vitesse angulaire et déplacement
Rotation et systèmes matériels
15.1K Vues

10.2 : Vitesse angulaire et accélération
Rotation et systèmes matériels
9.1K Vues

10.3 : Mouvement de rotation uniformément varié - I
Rotation et systèmes matériels
6.7K Vues

10.4 : Mouvement de rotation uniformément varié - II
Rotation et systèmes matériels
5.9K Vues

10.5 : Établir une relation entre le mouvement linéaire et le mouvement angulaire - I
Rotation et systèmes matériels
6.5K Vues

10.6 : Établir une relation entre le mouvement linéaire et le mouvement angulaire - II
Rotation et systèmes matériels
5.4K Vues

10.7 : Moment d'inertie
Rotation et systèmes matériels
12.0K Vues

10.8 : Moment d'inertie et énergie cinétique de rotation
Rotation et systèmes matériels
7.3K Vues

10.9 : Moment d'inertie : calculs
Rotation et systèmes matériels
6.7K Vues

10.11 : Théorème des axes parallèles (théorème de Huygens)
Rotation et systèmes matériels
6.5K Vues

10.12 : Théorème de l’axe perpendiculaire
Rotation et systèmes matériels
2.7K Vues

10.13 : Transformation vectorielle dans les systèmes de coordonnées en rotation
Rotation et systèmes matériels
1.5K Vues

10.14 : Coriolis Force
Rotation et systèmes matériels
3.1K Vues