23.7 : Gauss's Law: Planar Symmetry
A planar symmetry of charge density is obtained when charges are uniformly spread over a large flat surface. In planar symmetry, all points in a plane parallel to the plane of charge are identical with respect to the charges. Suppose the plane of the charge distribution is the xy-plane, and the electric field at a space point P with coordinates (x, y, z) is to be determined. Since the charge density is the same at all (x, y) - coordinates in the z = 0 plane, by symmetry, the electric field at P cannot depend on the x- or y-coordinates of point P. Therefore, the electric field at P can only depend on the distance from the plane and has a direction either toward the plane or away from the plane. That is, the electric field at P has only a nonzero z-component.
The electric field due to a planar charge distribution with surface charge density σ can be calculated using Gauss’s Law. For this, consider a cylindrical Gaussian surface that is equidistant from the plane on both sides. The cylinder's axis is perpendicular to the plane, and the area of its flat ends is A, as shown in the figure.
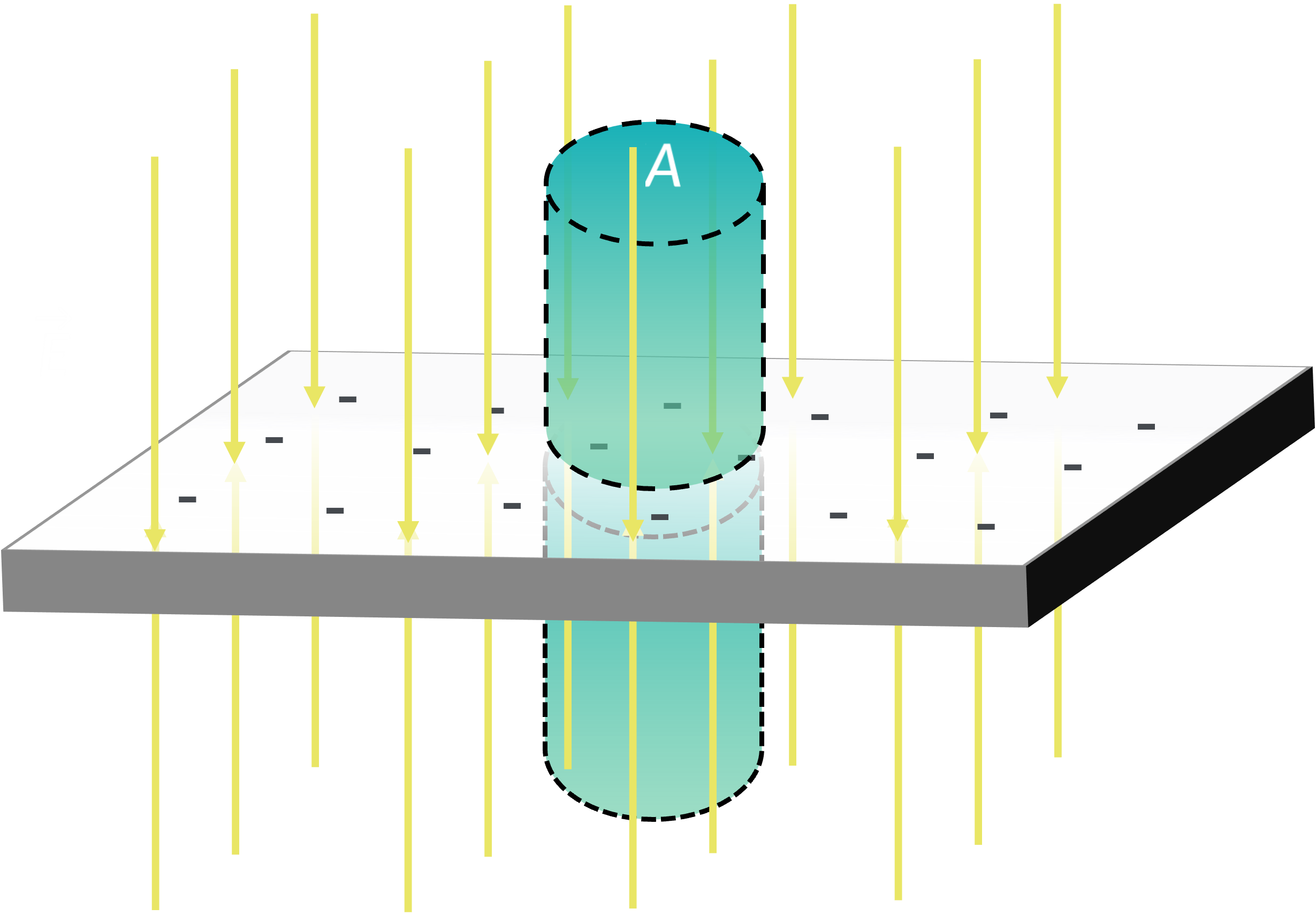
The electric flux through the curved surface of the cylinder is zero as the electric field is perpendicular to the area vector. The electric flux through the flat surface is EA, as the electric field in this plane is parallel to the area vector. Hence the total flux through the Gaussian surface is -2EA.
Now, the charge enclosed by the Gaussian surface is -σA. From Gauss’s law, the electric flux through the Gaussian surface is proportional to the charge enclosed by the surface.
Using the equations for the flux and Gauss's law, the electric field at a point P from the uniformly charged plane is given by
The direction of the electric field depends on the sign of the charge on the plane and the side of the plane where the field point P is located. From the above expression, the electric field is observed to be independent of the distance from the plane; this is an effect of the assumption that the plane is infinite. In practical terms, the result given above is still a useful approximation for finite planes near the center.
Du chapitre 23:

Now Playing
23.7 : Gauss's Law: Planar Symmetry
Gauss's Law
7.8K Vues

23.1 : Flux électrique
Gauss's Law
7.7K Vues

23.2 : Calcul du flux électrique
Gauss's Law
1.7K Vues

23.3 : Loi de Gauss
Gauss's Law
7.1K Vues

23.4 : Loi de Gauss : résolution de problèmes
Gauss's Law
1.6K Vues

23.5 : Loi de Gauss : symétrie sphérique
Gauss's Law
7.4K Vues

23.6 : Loi de Gauss : symétrie cylindrique
Gauss's Law
7.4K Vues

23.8 : Champ électrique à l’intérieur d’un conducteur
Gauss's Law
5.9K Vues

23.9 : Charge sur un conducteur
Gauss's Law
4.4K Vues

23.10 : Champ électrique à la surface d’un conducteur
Gauss's Law
4.6K Vues

23.11 : Champ électrique d’une sphère non uniformément chargée
Gauss's Law
1.4K Vues

23.12 : Champ électrique des plaques conductrices parallèles
Gauss's Law
871 Vues

23.13 : Divergence et courbure du champ électrique
Gauss's Law
5.4K Vues