Modélisation computationnelle des neurones rétiniens pour la recherche sur les prothèses visuelles - Approches fondamentales

Résumé

Nous résumons un flux de travail pour modéliser informatiquement les comportements d’un neurone rétinien en réponse à une stimulation électrique. Le modèle informatique est polyvalent et comprend des étapes d’automatisation utiles pour simuler une gamme de scénarios physiologiques et anticiper les résultats des futures études in vivo / in vitro .

Résumé

La modélisation informatique est devenue une méthode de plus en plus importante en ingénierie neuronale en raison de sa capacité à prédire les comportements des systèmes in vivo et in vitro . Cela a le principal avantage de minimiser le nombre d’animaux requis dans une étude donnée en fournissant une prédiction souvent très précise des résultats physiologiques. Dans le domaine de la prothèse visuelle, la modélisation informatique a un éventail d’applications pratiques, y compris l’information sur la conception d’un réseau d’électrodes implantables et la prédiction des percepts visuels qui peuvent être obtenus par la délivrance d’impulsions électriques dudit réseau. Certains modèles décrits dans la littérature combinent une morphologie tridimensionnelle (3D) pour calculer le champ électrique et un modèle de câble du neurone ou du réseau neuronal d’intérêt. Afin d’accroître l’accessibilité de cette méthode en deux étapes pour les chercheurs qui peuvent avoir une expérience préalable limitée en modélisation informatique, nous fournissons une vidéo des approches fondamentales à adopter afin de construire un modèle informatique et de l’utiliser pour prédire les résultats physiologiques et psychophysiques des protocoles de stimulation déployés via une prothèse visuelle. Le guide comprend les étapes de construction d’un modèle 3D dans un logiciel de modélisation par éléments finis (FEM), la construction d’un modèle de cellules ganglionnaires de la rétine dans un logiciel de calcul de neurones multicompartimentaux, suivie de la fusion des deux. Un logiciel de modélisation par éléments finis pour résoudre numériquement des équations physiques serait utilisé pour résoudre la distribution du champ électrique dans les stimulations électriques des tissus. Ensuite, un logiciel spécialisé pour simuler les activités électriques d’une cellule ou d’un réseau neuronal a été utilisé. Pour suivre ce tutoriel, une connaissance du principe de fonctionnement d’une neuroprothèse, ainsi que des concepts neurophysiologiques (par exemple, le mécanisme du potentiel d’action et une compréhension du modèle de Hodgkin-Huxley), serait nécessaire.

Introduction

Les neuroprothèses visuelles sont un groupe de dispositifs qui délivrent des stimulations (électriques, lumineuses, etc.) aux cellules neurales dans la voie visuelle pour créer des phosphènes ou la sensation de voir la lumière. Il s’agit d’une stratégie de traitement qui est utilisée en clinique depuis près d’une décennie pour les personnes atteintes de cécité permanente causée par des maladies dégénératives de la rétine. En règle générale, un système complet comprend une caméra externe qui capture les informations visuelles autour de l’utilisateur, une unité d’alimentation et de calcul pour traiter et traduire l’image en une série d’impulsions électriques, et un réseau d’électrodes implantées qui interface le tissu neural et délivre les impulsions électriques aux cellules neurales. Le principe de fonctionnement permet de placer une neuroprothèse visuelle à différents endroits le long de la voie visuelle allant de la rétine au cortex visuel, à condition qu’elle soit en aval du tissu endommagé. La majorité des recherches actuelles en neuroprothèses visuelles se concentrent sur l’augmentation de l’efficacité de la stimulation et l’amélioration de l’acuité spatiale pour fournir une vision plus naturelle.

Dans les efforts visant à améliorer l’efficacité de la stimulation, la modélisation informatique a été une méthode rentable et rapide pour valider la conception d’une prothèse et simuler son résultat visuel. La modélisation informatique dans ce domaine a gagné en popularité depuis 1999 lorsque Greenberg¹ a modélisé la réponse d’une cellule ganglionnaire rétinienne à des stimuli électriques extracellulaires. Depuis lors, la modélisation informatique a été utilisée pour optimiser les paramètres de l’impulsion électrique^2,3 ou la conception géométrique de l’électrode ^4,5. Malgré la variation de la complexité et des questions de recherche, ces modèles fonctionnent en déterminant la distribution de tension électrique dans le milieu (par exemple, le tissu neural) et en estimant la réponse électrique que les neurones à proximité produiront en raison de la tension électrique.

La distribution de tension électrique dans un conducteur peut être trouvée en résolvant les équations de Poisson⁶ à tous les endroits:

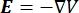
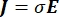
où E est le champ électrique, V le potentiel électrique, J la densité de courant et σ est la conductivité électrique. Le 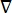dans l’équation indique un opérateur de gradient. Dans le cas d’un courant stationnaire, les conditions aux limites suivantes sont imposées au modèle:

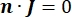
où n est la normale à la surface, Ω représente la frontière, et I₀ représente le courant spécifique. Ensemble, ils créent une isolation électrique aux limites extérieures et créent une source de courant pour une limite sélectionnée. Si nous supposons une source ponctuelle monopolaire dans un milieu homogène avec une conductivité isotrope, le potentiel électrique extracellulaire à un endroit arbitraire peut être calculé par⁷:

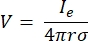
où I_e est le courant et est la distance entre l’électrode et le point de mesure. Lorsque le support est inhomogène ou anisotrope, ou que le réseau d’électrodes comporte plusieurs électrodes, une suite de calcul pour résoudre numériquement les équations peut être pratique. Un logiciel de modélisation par éléments finis⁶ décompose le conducteur de volume en petites sections appelées « éléments ». Les éléments sont interconnectés les uns avec les autres de sorte que les effets du changement dans un élément influencent le changement dans les autres, et cela résout les équations physiques qui servent à décrire ces éléments. Avec la vitesse de calcul croissante des ordinateurs modernes, ce processus peut être achevé en quelques secondes. Une fois le potentiel électrique calculé, on peut alors estimer la réponse électrique du neurone.

Un neurone envoie et reçoit des informations sous forme de signaux électriques. Ces signaux se présentent sous deux formes: les potentiels gradués et les potentiels d’action. Les potentiels gradués sont des changements temporaires du potentiel de membrane dans lesquels la tension à travers la membrane devient plus positive (dépolarisation) ou négative (hyperpolarisation). Les potentiels gradués ont généralement des effets localisés. Dans les cellules qui les produisent, les potentiels d’action sont des réponses tout ou rien qui peuvent parcourir de longues distances le long d’un axone. Les potentiels gradués et d’action sont sensibles à l’environnement électrique et chimique. Un pic de potentiel d’action peut être produit par divers types de cellules neuronales, y compris les cellules ganglionnaires de la rétine, lorsqu’un seuil de potentiel transmembranaire est franchi. Le pic et la propagation du potentiel d’action déclenchent alors la transmission synaptique des signaux aux neurones en aval. Un neurone peut être modélisé comme un câble divisé en segments cylindriques, où chaque segment a une capacité et une résistance dues à la membrane bicouche^{lipidique 8}. Un programme de calcul neuronal⁹ peut estimer l’activité électrique d’une cellule électriquement excitable en discrétisant la cellule en plusieurs compartiments et en résolvant le modèle mathématique¹⁰:

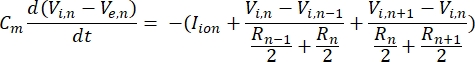
Dans cette équation, C_mest la capacité de la membrane, V _e,n est le potentiel extracellulaire au nœud n, V_i,n le potentiel intracellulaire au nœud n, R n la résistance intracellulaire (longitudinale) au nœud n, et I_ion est le courant ionique traversant les canaux ioniques au nœud _n. Les valeurs de V du modèle FEM sont implémentées sous forme de V_e,n pour tous les nœuds du neurone lorsque la stimulation est active.

Les courants transmembranaires des canaux ioniques peuvent être modélisés à l’aide des formulations de Hodgkin-Huxley¹¹:

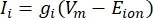
où g i est la conductance spécifique du canal, V _m le potentiel transmembranaire (V _i,n - V_e,n) et E_ion le potentiel d’inversion du canal ionique. Pour les canaux voltage-dépendants, tels que le canal Na, les paramètres sans dimension, m et h, qui décrivent la probabilité d’ouverture ou de fermeture des canaux sont introduits:

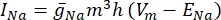
où 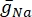est la conductance maximale de la membrane pour le canal ionique particulier, et les valeurs des paramètres m et h sont définies par des équations différentielles:

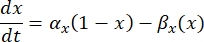
où α x et β_x sont des fonctions dépendantes de la tension qui définissent les constantes de vitesse du canal ionique. Elles prennent généralement la forme :

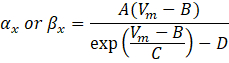
Les valeurs des paramètres de ces équations, y compris la conductance maximale, ainsi que les constantes A, B, C et D, ont généralement été trouvées à partir de mesures empiriques.

Avec ces blocs de construction, des modèles de différentes complexités peuvent être construits en suivant les étapes décrites. Un logiciel FEM est utile lorsque l’équation de Poisson ne peut pas être résolue analytiquement, comme dans le cas d’une conductance inhomogène ou anisotrope dans le conducteur de volume ou lorsque la géométrie du réseau d’électrodes est complexe. Une fois que les valeurs de potentiel extracellulaire ont été résolues, le modèle de câble neuronal peut alors être résolu numériquement dans le logiciel de calcul neuronal. La combinaison des deux logiciels permet le calcul d’une cellule ou d’un réseau neuronal complexe à un champ électrique non uniforme.

Un modèle simple en deux étapes d’une cellule ganglionnaire rétinienne sous stimulation suprachoroïdienne sera construit à l’aide des programmes susmentionnés. Dans cette étude, la cellule ganglionnaire de la rétine sera soumise à une gamme d’amplitudes d’impulsions de courant électrique. L’emplacement de la cellule par rapport au stimulus est également varié pour montrer la relation distance-seuil. De plus, l’étude comprend une validation du résultat de calcul par rapport à une étude in vivo du seuil d’activation corticale utilisant différentes tailles d’électrode de stimulation¹², ainsi qu’une étude in vitro montrant la relation entre la distance électrode-neurone et le seuil d’activation¹³.

Protocole

1. Mise en place du modèle d’éléments finis pour les calculs de potentiel électrique

1. Déterminer les étapes de simulation et la complexité du modèle
   NOTE: Le but de la première étape est de clarifier le but de la modélisation, qui déterminera les éléments nécessaires du modèle et de la procédure de simulation. Un point important à considérer est le comportement des cellules neurales qui doit être montré par le modèle, et quel protocole de test serait nécessaire pour démontrer ce comportement. Cette étude montre une relation distance-seuil pour un neurone stimulé extracellulairement, ainsi que la courbe taille-seuil de l’électrode. Pour ce faire, un modèle de cellule neuronale compartimenté en différentes sections (pour incorporer la variation des paramètres morphologiques et biophysiques dans le neurone) sensibles à la tension extracellulaire et la simulation d’une gamme de tailles et de positions d’électrodes sont nécessaires.
   1. Définir la question de recherche et les variables expérimentales.
      1. Définir une question de recherche et un protocole de test pour guider la construction du modèle. Il est préférable de commencer par une question claire et de construire un modèle aussi simple que possible pour y répondre.
   2. Déterminer les éléments nécessaires à inclure dans le modèle complet
      REMARQUE: Dans cette approche de modélisation, la cellule est considérée comme immergée dans un milieu électriquement conducteur, c’est-à-dire le tissu biologique. La stimulation électrique se produit à travers ce « conducteur de volume », c’est-à-dire le milieu, ce qui entraîne une distribution du potentiel électrique.
      1. Sur la base des questions de recherche et des variables à résoudre, décidez si les deux éléments (modèle FEM et modèle de câble neuronal) sont nécessaires. Si, par exemple, la modélisation a besoin d’une seule électrode qui peut être simplifiée en tant que source ponctuelle et que le milieu est homogène, un FEM peut ne pas être nécessaire, et un calcul analytique du champ électrique extracellulaire peut être effectué pour le remplacer.
2. Téléchargez et installez le logiciel
   NOTE: L’étude a utilisé les versions des applications logicielles (COMSOL, NEURON et Python Anaconda) et du matériel spécifié dans le tableau des matériaux. Il peut y avoir des différences mineures dans les étapes ou les résultats si différentes versions du logiciel / matériel sont utilisées.
   1. Téléchargez le logiciel adapté au système d’exploitation de l’ordinateur et achetez une licence, si nécessaire. Assurez-vous que tous les modules de simulation requis sont téléchargés et installez tous les logiciels.
3. Recueillir les données sur l’anatomie du tissu et de la cellule à modéliser
   NOTE: Pour cette méthode, les paramètres anatomiques et biophysiques ont été tirés de résultats empiriques. Il est courant que les modèles informatiques mélangent des paramètres mesurés chez différentes espèces en raison de l’indisponibilité des données. Pour une simulation de stimulation suprachoroïdienne, les couches tissulaires entre les électrodes stimulantes et de référence doivent être incluses dans le modèle.
   1. Recueillir l’anatomie du tissu à partir d’études histologiques.
      1. Dans ce modèle, incluez la choroïde, le tissu rétinien et les domaines vitré, où chaque domaine est modélisé comme un prisme rectangulaire pour faciliter la construction du modèle. Recueillir l’épaisseur moyenne du tissu rétinien à partir des données histologiques publiées¹⁴ pour l’utiliser ultérieurement comme hauteur de chaque prisme.
   2. Recueillir les données morphologiques d’une seule cellule à partir de la coloration cellulaire ou de la base de données publique de neurones.
      1. Téléchargez la morphologie détaillée des neurones à partir d’une base de données telle que NeuroMorpho.org, qui fournit une fonction de métadonnées de recherche pour trouver le neurone pertinent en fonction de l’espèce, de la région du cerveau, du type de cellule, etc. Pour cette étude, trouvez le modèle OFF RGC (D23WM13_27_1-OffRGC_msa)¹⁵ de Guo en entrant Lapin > Blanc de Nouvelle-Zélande dans le champ Espèce et Rétine dans le champ Région du cerveau . Cliquez sur le modèle et téléchargez le fichier .swc.
4. Recueillir les données biophysiques de la cellule modélisée
   NOTE: Les paramètres biophysiques comprennent les valeurs de conductivité électrique pour chaque couche tissulaire et les paramètres électriques de la membrane neurale et des canaux ioniques.
   1. En raison de la disponibilité des données, utiliser les valeurs de conductivité électrique qui ont été prises sur le lapin¹⁶ pour le modèle tissulaire, tandis que la dynamique des canaux ioniques était basée sur le modèle de Sheasby et Fohlmeister de la rétine de la salamandre tigrée¹⁷.
5. Construire la géométrie du modèle d’éléments finis du tissu et de l’électrode dans le logiciel FEM
   REMARQUE: La géométrie du tissu et du réseau d’électrodes affecte la distribution du potentiel électrique, qui à son tour influence le comportement des cellules neurales. Par conséquent, il est important de construire une géométrie réaliste du milieu où résident les cellules, ainsi que de l’électrode. Le logiciel FEM utilisé dans ce tutoriel dispose d’une interface graphique qui permet de construire facilement la géométrie du modèle.
   1. Configuration du modèle FEM dans l’interface graphique du logiciel :
      1. Exécutez le logiciel FEM et cliquez sur Model Wizard > 3D. Dans la zone de liste Sélectionner la physique , développez les champs électriques AC/DC > et courant > courants électriques (ec), puis cliquez sur Ajouter. Cliquez sur Étude et ajoutez une étude stationnaire sous l’option Études générales , puis cliquez sur Terminé (Figure supplémentaire 1).
   2. Configuration de l’unité et des paramètres géométriques de l’électrode.
      1. Dans l’arborescence Model Builder, cliquez sur Paramètres 1. Dans le tableau, tapez 'elec_rad' dans le champ Nom et '50' dans le champ Expression pour créer une électrode de 50 unités de rayon. Ensuite, cliquez sur Géométrie et changez l’unité de longueur en μm, car le soma d’une cellule ganglionnaire rétinienne typique mesure environ 10 μm de diamètre (Figure supplémentaire 2).
   3. Créer les couches de tissus à l’aide de domaines de blocs
      REMARQUE: Pour construire la géométrie du modèle, trois blocs pour représenter différentes structures dans l’œil ont été utilisés. Le bloc 1 représentait la choroïde, le bloc 2 le tissu rétinien et le bloc 3 le vitré.
      1. Cliquez avec le bouton droit sur Géométrie 1 > Bloc pour créer un domaine de bloc. Répétez cette étape deux fois de plus pour créer trois blocs au total. Pour tous les blocs, définissez la profondeur et la largeur sur 5 000 μm et remplacez l’option Base (sous Position) par Centrer. Affectez les valeurs Hauteur (sous Taille et Forme) et z (sous Position) suivantes pour chaque bloc :
         Bloc 1 : Hauteur = 112 μm, z = 0 μm
         Bloc 2 : Hauteur = 151 μm, z = 131,5 μm
         Bloc 3 : Hauteur = 5 000 μm, z = 2 707 μm
   4. Création d’un plan de travail pour ajouter une électrode au modèle
      1. Cliquez avec le bouton droit de la souris sur Géométrie 1 dans l’arbre du modèle, puis choisissez Plan de travail. Cliquez sur Plan de travail 1 et changez le Type de plan en Parallèle de face, cliquez sur le bouton Activer la sélection sous le Type de plan et choisissez la surface inférieure du bloc 1 (blk 1 > 1).
   5. Dessin d’une électrode de disque sur le plan de travail
      1. Cliquez sur Géométrie plane sous Plan de travail 1 et cliquez sur Esquisse dans la barre d’outils principale. Sélectionnez Cercle, cliquez n’importe où dans le rectangle dans l’onglet Graphiques , puis faites glisser pour créer une électrode de disque. Changez le rayon à 'elec_rad' μm, xw et yw à 0 μm, puis cliquez sur Construire tout.
   6. Affectation des propriétés des matériaux à chaque domaine
      REMARQUE: En suivant les étapes pour construire la géométrie, le modèle serait séparé en plusieurs « domaines », qui sont des pièces 3D individuelles qui composent la géométrie complète. Une valeur de conductivité électrique doit être attribuée à chaque domaine pour calculer la distribution du champ électrique dans l’ensemble du modèle.
      1. Dans l’arbre du modèle, cliquez avec le bouton droit sur Matériau > Matériau vierge, puis cliquez sur Matériau 1 et modifiez la sélection en Manuel.
      2. Cliquez sur les domaines dans la fenêtre graphique afin que seul le domaine 1 soit choisi. Choisissez Propriétés du matériau > Propriétés de base > conductivité électrique, cliquez sur le bouton Ajouter au matériau et modifiez la valeur de conductivité électrique à la valeur à 0,043 S/m¹⁵.
      3. Répétez les étapes pour les domaines 2 et 3, avec des valeurs de conductivité électrique de 0,7 16 et 1,55¹⁶ S/m, respectivement (figure supplémentaire 3).
   7. Maillage d’un modèle 3D : Pour mailler le modèle, accédez à l’arbre du modèle et cliquez avec le bouton droit de la souris sur Mesh 1 > Free Tetrahedral. Cliquez sur Tétraédrique gratuit 1 et choisissez Tout construire.
      REMARQUE: Le processus de maillage décompose l’ensemble de la géométrie en « éléments » plus petits (un élément est un segment virtuel de la géométrie du modèle où les équations physiques sont résolues numériquement). Le maillage avec des éléments plus petits augmente théoriquement la précision de l’approximation, mais est exhaustif sur le plan informatique. Une pratique courante consiste à commencer le modèle avec un maillage clairsemé et à enregistrer le résultat de la simulation, puis à répéter continuellement la simulation avec des éléments de maillage plus petits à chaque fois et à comparer les résultats. Le processus d’affinement peut s’arrêter lorsqu’il n’y a pas de différence significative dans les résultats de calcul des étapes d’affinement suivantes.
      1. Évaluation de la qualité du maillage : cliquez avec le bouton droit de la souris sur Mesh 1 et choisissez Statistiques pour afficher l’histogramme de la qualité de l’élément. Suivez les étapes de raffinage du maillage ci-dessous pour améliorer la qualité des éléments.
         Remarque : L’utilisation du maillage par défaut peut produire de nombreux éléments de mauvaise qualité, ce qui rend les calculs inexacts. Dans la plupart des cas, un certain degré de raffinement du maillage est nécessaire.
      2. Affiner le maillage autour du périmètre de l’électrode
         REMARQUE: Les zones où il pourrait y avoir des changements brusques dans le champ électrique nécessitent généralement un maillage plus raffiné. Ici, un maillage plus dense autour du périmètre de l’électrode a été ajouté à l’aide de la fonction de distribution des bords.
         1. Tout d’abord, supprimez le maillage Tétraédrique libre 1 existant. Ensuite, faites un clic droit sur Mesh 1 > Distribution, cliquez sur Distribution 1, changez le niveau d’entité géométrique en Edge et choisissez Edges 19-22 (le périmètre de l’électrode du disque).
         2. Définissez le type de distribution sur Nombre fixe d’éléments et modifiez le champ Nombre d’éléments sur elec_rad*3/10 pour rendre les éléments raisonnablement petits.
      3. Affiner le maillage à travers la choroïde et le tissu rétinien
         1. Dans l’arbre du modèle, cliquez avec le bouton droit de la souris sur Mesh 1 > Swept. Cliquez sur Balayé 1. Choisissez Domaines 1 et 2. Ensuite, faites un clic droit sur Mesh 1 > Free Tetrahedral, définissez le niveau d’entité géométrique sur Remaining, puis cliquez sur Build All. (Facultatif : Vérifiez à nouveau l’histogramme de la qualité des éléments pour vous assurer que les éléments de faible qualité ont été réduits proportionnellement).
6. Appliquer la physique au modèle des éléments finis
   REMARQUE: La « physique » dans le logiciel FEM sont des ensembles d’équations mathématiques et de conditions aux limites qui doivent être assignés au modèle. C’est le calcul de la solution à l’ensemble simultané d’équations qui est effectué au cours de l’exécution du modèle. Le choix de la physique à appliquer à la géométrie dépend du phénomène physique simulé. Par exemple, la physique des courants électriques, telle qu’elle est utilisée dans ce modèle, observe la distribution du champ électrique et néglige le phénomène magnétique (inductif). D’autres formes de physique pourraient être appliquées à la géométrie si d’autres problèmes physiques (par exemple, la distribution de la température, les contraintes mécaniques, etc.) doivent être résolus.
   1. Sélection de la physique et application des conditions aux limites
      REMARQUE : Si une impulsion de tension constante doit être appliquée, la condition aux limites du potentiel flottant doit être remplacée par une condition aux limites du potentiel électrique.
      1. Développez Courants électriques 1 dans l’arbre du modèle et vérifiez si Conservation du courant 1, Isolation électrique 1 et Valeurs initiales 1 sont répertoriés. Ensuite, cliquez avec le bouton droit de la souris sur les courants électriques 1 > masse (cela assigne 0 V à un plan distant, simulant une électrode de référence distante) et appliquez-le à la surface la plus éloignée de l’électrode (Surface 10).
      2. Ensuite, faites un clic droit sur le potentiel flottant de courants électriques 1 > (cela simule une source de courant à courant constant), assigné à l’électrode du disque (surface 14), et modifiez la valeur I ₀ à 1 [μA] pour appliquer un courant unitaire.
   2. Exécution de la simulation avec un balayage paramétrique.
      REMARQUE: Cette étape exécutera la simulation et un balayage paramétrique a été ajouté, où plusieurs simulations ont été effectuées avec la valeur d’un paramètre modifiée dans chaque simulation. Ici, le paramètre de rayon d’électrode a été balayé et la distribution du potentiel électrique pour chaque simulation a été stockée dans le fichier modèle. Une fois la simulation exécutée, la branche Résultats de l’arbre du modèle a été renseignée avec un graphique multicoupes à potentiel électrique (ec).
      1. Dans l’arbre du modèle, cliquez avec le bouton droit sur Study 1 > Parametric Sweep. Cliquez sur Parametric Sweep (Balayage paramétrique) et, dans le tableau Study Setting (Paramètres de l’étude ), cliquez sur Add ( Ajouter), puis choisissez elec_rad pour le nom du paramètre.
      2. Tapez « 50, 150, 350, 500 » pour la liste des valeurs des paramètres et « μm » pour l’unité de paramètre, puis cliquez sur Calculer pour exécuter l’étude (Figure supplémentaire 4).

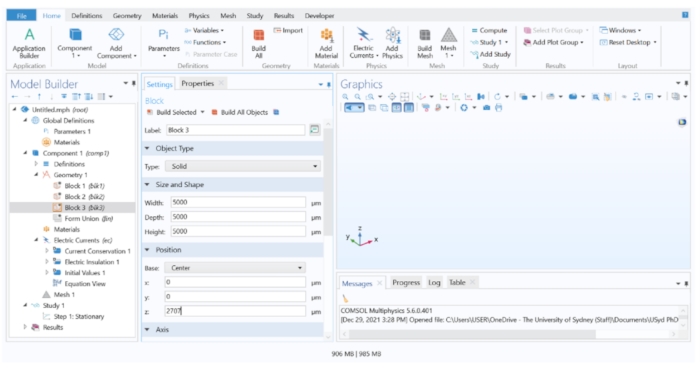
Figure 1 : Création de la géométrie tisssue. Une géométrie de bloc a été insérée dans le modèle FEM pour représenter le tissu. Veuillez cliquer ici pour voir une version agrandie de cette figure.

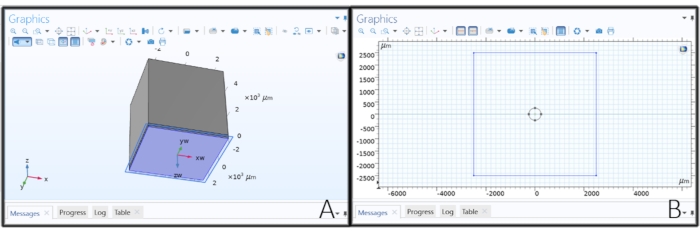
Figure 2 : Création de la géométrie de l’électrode. (A) Création d’un plan de travail pour dessiner l’électrode du disque. (B) Esquisse d’un cercle sur un plan de travail pour créer une électrode de disque. Veuillez cliquer ici pour voir une version agrandie de cette figure.

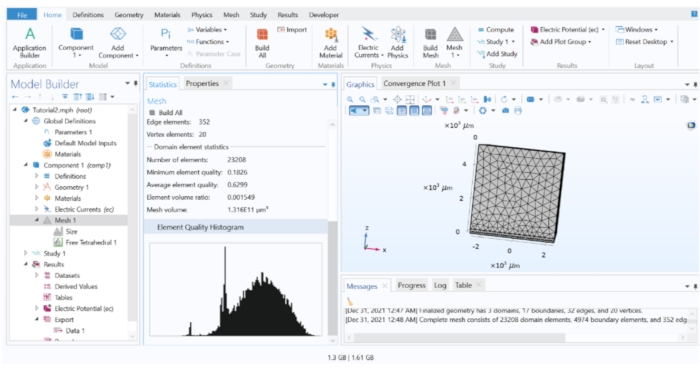
Figure 3 : Histogramme de la qualité des éléments du modèle FEM. L’histogramme a montré la qualité des éléments tout au long du modèle. Des améliorations du maillage sont nécessaires si une partie importante des éléments se trouvent dans la région de faible qualité. Veuillez cliquer ici pour voir une version agrandie de cette figure.

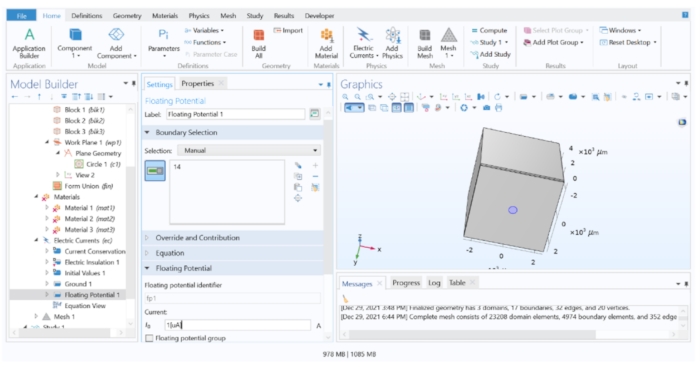
Figure 4 : Attribution d’une valeur de courant à l’électrode. Courant unitaire appliqué à la géométrie de l’électrode dans le logiciel FEM. Veuillez cliquer ici pour voir une version agrandie de cette figure.

2. Importation de la géométrie de la cellule neurale dans l’interface graphique de la suite de calcul neuronal

1. Construire la géométrie du modèle de cellule
   1. Importation de la morphologie à l’aide de la fonctionnalité Cell Builder.
      1. Exécutez 'nrngui' à partir du dossier d’installation de la suite de calcul neuron, cliquez sur Outils > Divers > Importer 3D, puis cochez la case Choisir un fichier .
      2. Localisez le fichier .swc téléchargé et cliquez sur Lire. Une fois la géométrie importée, cliquez sur Exporter > Cell Builder (Figure supplémentaire 5).
   2. Création d’un fichier .hoc de la morphologie cellulaire importée
      1. Allez dans l’onglet Sous-ensembles et observez les sous-ensembles qui ont été prédéfinis dans le modèle (par exemple, soma, axone, basal, etc.). Cochez la case Création continue , accédez à Gestion > Exportation et exportez la morphologie sous 'rgc.hoc'.
   3. Visualisation de la morphologie de la cellule
      1. Cliquez sur Tool > Model View > 1 Real Cells > Root Soma[0] dans la barre d’outils, cliquez avec le bouton droit de la souris sur la fenêtre qui apparaît et cliquez sur Type d’axe > Axe de vue. Par inspection visuelle, le diamètre du champ dendritique de ce modèle est d’environ 250 μm. Fermez les fenêtres NEURON pour l’instant.

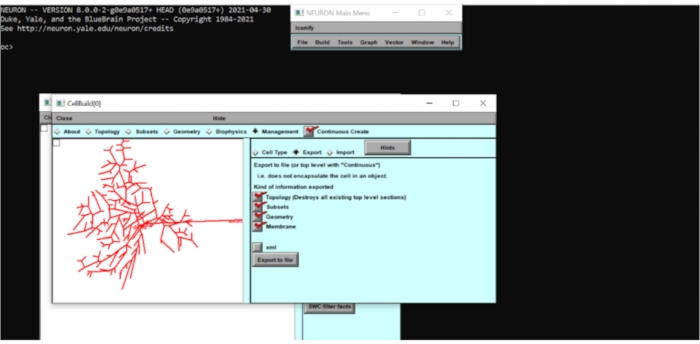
Figure 5 : Exportation des informations du modèle neuronal sous forme de fichier .hoc. La géométrie du neurone a été exportée vers un fichier .hoc pour permettre d’autres modifications. Veuillez cliquer ici pour voir une version agrandie de cette figure.

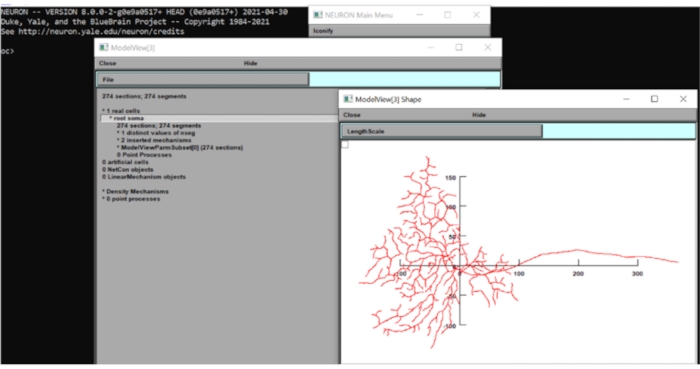
Figure 6 : Mesure de la dimension du neurone. La morphologie du neurone (vue de dessus) a été affichée dans l’interface graphique de la suite informatique neuronale avec les axes x-y superposés. L’échelle était en μm. Veuillez cliquer ici pour voir une version agrandie de cette figure.

3. Programmation de la simulation de calcul NEURON

1. Ajuster la morphologie de la cellule par programmation en langage .hoc
   REMARQUE: La morphologie de la cellule peut être ajustée via la fonction Cell Builder de l’interface graphique. Cependant, comment cela pourrait être fait en éditant le fichier .hoc pour accélérer le processus est démontré. Le fichier .hoc définit la topologie (connexions physiques entre chaque partie des neurones), la morphologie (la longueur, le diamètre et l’emplacement de chaque section de neurone) et les propriétés biophysiques (paramètres du canal ionique) de la cellule modélisée. La documentation complète pour la programmation .hoc peut être trouvée dans: https://neuron.yale.edu/neuron/static/new_doc/index.html#,
   1. Ouvrez le fichier .hoc résultant avec un éditeur de texte (par exemple, le Bloc-notes). Ajouter un segment initial axonale de 40 μm de longueur et un segment axonal étroit de 90 μm de longueur près du soma comme décrit dans Sheasby et Fohlmeister¹⁷, et modifier la longueur des dendrites de sorte que la taille du champ dendritique devienne 180 μm pour correspondre à la cellule G1 de Rockhill, et ^al.18.
      1. Création de nouvelles sections de cellules et définition des connexions topologiques pour chaque section.
         1. Pour créer de nouvelles sections de cellule pour le segment initial axonal (AIS) et le segment axonal étroit (NS), ajoutez ces lignes au début du fichier rgc.hoc :
            créer AIS, NS // Déclaration de compartiments cellulaires appelés AIS et NS
            Ensuite, remplacez la ligne 'connect axon(0), soma[1](1)' par:
            connect ais(0), soma[1](1) // Connexion du premier segment d’AIS à la fin de soma[1]
            connect ns(0), ais(1) // Connexion du premier segment de NS à la fin de l’AIS
            connect axon(0), ns(1) // Connexion du premier segment de l’axone à l’extrémité de NS
      2. Définition des positions, diamètres et longueurs 3D des sections de cellule
         1. Définissez les positions et diamètres 3D des compartiments AIS et NS en écrivant ces lignes à l’intérieur des crochets 'proc shape3d_31()':
            ais { pt3dadd(-2.25, -1.55, 0, 1) // Les trois premiers nombres sont la coordonnée xyz, et le diamètre est 1 μm
            pt3dadd(37.75, -1.55, 0, 1)} // Le premier point est à x = -2,25 μm et le dernier point est à x = 37,75 μm
            ns { pt3dadd(37.75, -1.55, 0, 0.3) // Les coordonnées 3D et le diamètre des segments NS
            pt3dadd(127.75, -1.55, 0, 0.3)}
         2. À la fin du fichier, déplacez les coordonnées 3D de l’axone afin que son point initial rencontre le point final de NS en tapant :
            axone {for i=0,n3d()-1 {pt3dchange(i, x3d(i)+130, y3d(i),z3d(i)-5, diam3d(i))}} //Décaler la coordonnée x
         3. A la fin du fichier, raccourcissez les compartiments dendritiques de 18% en tapant :
            forsec basal {L=L*0.82} // Mise à l’échelle de la longueur pour réduire la taille du champ dendritique
            define_shape() // Remplissage des informations 3D manquantes
2. Définition du nombre de segments pour chaque section
   REMARQUE: Chaque section du neurone peut être discrétisée spatialement, un peu comme le processus de maillage dans le modèle FEM. La discrétisation spatiale divise le neurone pratiquement en segments plus petits où les calculs doivent être effectués. Pour le nombre de segments 'nseg', assurez-vous que les nombres impairs sont utilisés pour vous assurer qu’il existe un nœud interne au milieu d’une section de cellule et essayez de tripler le nombre nseg jusqu’à ce que le calcul produise un résultat cohérent⁹. Un plus grand nombre de segments produira une approximation numérique plus précise, mais augmentera également la charge de calcul.
   1. Pour illustrer le processus de discrétisation, ajoutez les lignes suivantes dans le fichier rgc.hoc pour diviser les sections neuronales dans les sous-ensembles somatiques et axonaux en plusieurs segments:
      Forsec Somatic {nseg=31}
      forsec axonal {nseg=301}
      D’autres sections du modèle doivent également être discrétisées en tapant ces lignes, mais en changeant le nom du sous-ensemble (après 'forsec') et le nombre de segments (après 'nseg') comme souhaité.
3. Insérer des mécanismes de canal ionique personnalisés
   1. Écriture de mécanismes de canal ionique personnalisés en tant que fichiers .mod : Pour appliquer les mécanismes de canal ionique, créez des fichiers .mod et insérez les fichiers dans la partie section biophysique du fichier .hoc en suivant les étapes 3.3.1-3.3.3. Le fichier .mod contient les variables et les équations différentielles à résoudre pour chaque canal ionique.
      REMARQUE: Les définitions et les implémentations correctes du mécanisme des canaux ioniques sont essentielles pour des simulations précises des neurones. Lors de l’écriture de fichiers .mod, vérifiez si les unités sont correctes (l’utilitaire 'modlunit' fourni qui peut être exécuté pour vérifier la cohérence des unités) et que les équations sont écrites correctement. Pour tester que les mécanismes des canaux ioniques sont corrects, le courant de chaque canal ionique pendant la stimulation intracellulaire ou extracellulaire peut être tracé et comparé aux résultats empiriques.
      1. Canaux ioniques voltage-dépendants
         Remarque : Un fichier .mod pour créer un canal ionique voltage-dépendant inclut généralement un bloc DÉRIVÉ qui a l’équation différentielle à résoudre, un bloc BREAKPOINT qui a les commandes pour résoudre les équations différentielles à l’aide d’une méthode d’approximation numérique choisie et des blocs PROCEDURE qui indiquent au programme de calculer les paramètres de contrôle (par exemple, mt, ht et d dans cet exemple). Ce code calculera les valeurs du courant ionique traversant le canal pour chaque pas de temps.
         1. Pour illustrer le processus, créez un canal Ca dépendant de la tension qui a des équations différentielles de premier ordre à résoudre pour les variables de contrôle.
         2. Ouvrez un nouveau fichier dans l’éditeur de texte et tapez les lignes dans le document Matériau supplémentaire-Définition d’un canal Cat dépendant de la tension. Enregistrez ce fichier sous Cat.mod dans le même dossier que le fichier .hoc. Ce processus doit être répété pour les autres canaux ioniques contenus dans le neurone modèle.
      2. Canaux ioniques dépendants de la tension et de la concentration
         1. La cinétique de certains canaux ioniques, tels que les canaux potassiques activés par le calcium dans les cellules ganglionnaires de la rétine, dépend de la concentration intracellulaire de calcium en plus de la tension transmembranaire¹⁹. Pour modéliser ce type de mécanisme, créez un fichier appelé KCa.mod et tapez les lignes comme indiqué dans Canaux ioniques supplémentaires dépendants de la tension et de la concentration. Dans ce fichier .mod, la variable 'cai', qui est définie comme la concentration interne d’ion Ca a été calculée, puis cette variable est utilisée dans l’équation pour calculer le courant iKCa.
   2. Compilation de fichiers .mod
      1. Compilez tous les fichiers .mod en exécutant l’utilitaire mknrndll de la suite de calcul neuronal à partir du dossier d’installation. Localisez le dossier où les fichiers .mod sont contenus et cliquez sur compiler pour créer des fichiers O et C. Après cela, les mécanismes peuvent être insérés dans ce modèle cellulaire.
   3. Application des fichiers .mod dans le fichier de modèle principal de NERON.
      NOTE: Outre l’insertion des canaux ioniques, la conductance maximale de Na a été définie pour le sous-ensemble « somatique » uniquement. Nous pourrions ajuster individuellement la conductance membranaire maximale pour différents segments neuronaux si nécessaire.
      1. Pour plus de concision, combinez tous les mécanismes de canal ionique dans un seul fichier .mod (Supplementary Material-Complete .mod file). Insérez le fichier .mod combiné contenant tous les canaux ioniques et un canal de fuite passif dans tous les segments du sous-ensemble 'somatique' en tapant les lignes ci-dessous dans la procédure 'biophys' du fichier rgc.hoc:
         forsec somatique {insert rgcSpike
         Insert PAS // canal de fuite passif
         gnabar_rgcSpike = 80e-3
         g_pas = 0,008e-3 // conductance de la membrane de fuite}
   4. Réglage de la résistivité axoplasmique
      1. Les cellules ont une résistivité axoplasmique qui peut être modifiée par compartiment. Pour ce modèle, tous les segments ont la même résistivité de 110 Ω·cm. Modifiez la résistivité axoplasmique dans le fichier rgc.hoc :
         forall {Ra = 110}
4. Insérer des mécanismes extracellulaires et définir la forme d’onde pulsée
   1. Insertion d’un mécanisme extracellulaire dans le modèle cellulaire
      1. Pour que le modèle de cellule réponde à la tension extracellulaire, insérez un mécanisme extracellulaire dans tous les segments en tapant la ligne au bas du fichier rgc.hoc :
         forall {insert extracellular}
   2. Création d’une impulsion biphasique
      Remarque : Dans cette démonstration, une impulsion biphasique à courant constant est créée qui est réglable par l’utilisateur en largeur d’impulsion, en intervalle interphase et en nombre de répétitions en créant une procédure dans un fichier .hoc. Pour un programme plus structuré, utilisez le fichier rgc.hoc comme fichier pour créer le modèle de cellule, tandis que le processus de stimulation est appliqué dans un fichier .hoc séparé, qui charge le modèle de cellule auquel la stimulation est appliquée.
      1. Créez un nouveau fichier texte appelé stimulation.hoc et démarrez le code en chargeant le fichier de modèle de cellule ; ensuite, faites une impulsion biphasique en définissant une procédure comme indiqué dans Matériel supplémentaire - Création d’une impulsion biphasique dans la simulation neuronale.
         REMARQUE: Cette étape crée une impulsion biphasique cathodique à courant constant où les paramètres de stimulus doivent être déclarés par l’utilisateur lors de l’exécution de la simulation. Actuellement, l’amplitude des impulsions anodiques et cathodiques est de ±1 μA, mais cette amplitude doit changer en fonction du courant de stimulation délivré par l’électrode du disque.

4. Exécution et automatisation de plusieurs simulations

1. Combinaison des modèles
   1. Extraction des coordonnées des nœuds dans le modèle de cellule neuronale
      NOTE: Le but de la combinaison des simulations est d’acquérir les valeurs de potentiel extracellulaire correspondant à chaque nœud du modèle cellulaire. Les coordonnées des deux modèles doivent cependant être alignées. Dans cet exemple, le segment central du soma (soma(0,5)) a été aligné pour se trouver sur le fond médian horizontal du tissu rétinien (correspondant à la couche de cellules ganglionnaires rétiniennes), avec le nœud central du soma situé juste au-dessus du centre de l’électrode du disque.
      1. Ouvrez le modèle FEM et notez la coordonnée d’un point de référence (par exemple, le plan médian horizontal du tissu rétinien, au-dessus du centre de l’électrode du disque), auquel cas elle est de [0, 0, 131,5] μm.
      2. Dans la suite de calcul neuronale, créez un fichier appelé calculateCoord.hoc pour extraire les coordonnées du centroïde de chaque segment et décaler chaque section de sorte que le segment central du soma ait la même coordonnée que le point de référence dans le modèle FEM (Supplementary Material-Calculation the coordinate of each node).
   2. Enregistrement des points de coordonnées dans un fichier texte
      1. Exécutez le fichier calculateCoord.hoc (soit en double-cliquant à partir de l’explorateur de fichiers, soit en ouvrant l’interface graphique de la suite de calcul neuronale; puis, cliquez sur Fichier > charger hoc dans la barre d’outils). Enregistrez les coordonnées des valeurs de tension extracellulaire à évaluer dans un fichier texte nommé 'coordonnées.dat'.
   3. Exécution des simulations et enregistrement des données de tension dans un fichier texte
      REMARQUE: Dans cette étape, nous avons extrait les valeurs extracellulaires calculées du modèle FEM, mais nous n’enregistrerions les données qu’à partir des coordonnées pertinentes qui coïncident avec le centre de chaque segment cellulaire. Suivez l’étape 4.1.6.2 lorsqu’un grand nombre de potentiels sont nécessaires pour exporter.
      1. Ouvrez le fichier de modèle de tissu dans le logiciel FEM ; allez à l’en-tête Résultats dans l’arbre du modèle, puis cliquez sur Exporter > données > données 1. Assurez-vous que le jeu de données est défini sur Étude 1/Solutions paramétriques 1, puis tapez « V » dans la colonne Expression et « mV » dans la colonne Unité .
      2. Sous Sortie, remplacez le nom de fichier par extracellulaire.dat puis choisissez Points à évaluer dans : À partir du fichier. Chargez les coordonnées.dat pour le champ Fichier de coordonnées , puis cliquez sur Exporter.
   4. Application de l’impulsion biphasique au modèle cellulaire
      REMARQUE: À ce stade, les valeurs de tension extracellulaire pour chaque segment de cellule à un point temporel (où le courant est de 1 μA) sont disponibles. Comme l’étude vise à soumettre la cellule à une impulsion biphasique, faites en sorte que la valeur de tension extracellulaire subie par la cellule change avec le temps en utilisant la méthode « vector.play ».
      1. Ajouter les lignes indiquées dans le Matériau supplémentaire-Application de l’impulsion biphasique dans le fichier stimulation.hoc.
   5. Exécution de la simulation combinée
      NOTE: Un intervalle de temps 'dt' pour les approximations numériques doit être défini pour exécuter les simulations. Semblable à nseg, un dt plus court peut augmenter la précision de calcul, mais augmente également le coût de calcul.
      1. Ajoutez les lignes indiquées dans la simulation de neurones Supplementary Material-Performing the neuron à la fin du fichier stimulation.hoc. Ensuite, double-cliquez sur le fichier stimulation.hoc pour charger le script et exécuter automatiquement la simulation. Le potentiel transmembranaire du segment d’intérêt peut être affiché dans l’interface graphique de la suite informatique neuronale (étape 4.2.1) ou enregistré dans un fichier texte pour être lu dans d’autres programmes (étape 4.1.6.1.2). Suivez les étapes 4.1.6.1 et 4.1.6.2 si des calculs répétés et un grand nombre de potentiels de membrane doivent être exportés.
   6. Extra: Automatisation des simulations
      REMARQUE: Pour trouver une amplitude de seuil, bouclez la simulation plusieurs fois avec une amplitude de courant différente à chaque fois. Une autre automatisation pourrait être nécessaire pour trouver le seuil pour les neurones situés à différentes positions par rapport à l’électrode stimulante. Une étape d’automatisation peut être effectuée dans la suite de calcul neuronal à l’aide d’une procédure, ainsi que dans le logiciel FEM à l’aide d’un script appelé « méthode ».
      1. Automatisation de la simulation de neurones pour trouver une amplitude seuil
         REMARQUE: Un lot de simulations de neurones peut être effectué automatiquement. Les étapes suivantes sont implémentées dans le programme de simulation de neurones pour trouver les amplitudes de seuil des neurones sous différents paramètres de stimulation.
         1. Créer une procédure pour répéter la simulation dans le programme de simulation de neurones : Dans le fichier stimulation.hoc, créez un vecteur contenant une plage d’amplitude de courant à tester. Ensuite, créez une procédure pour appliquer l’amplitude de courant et enregistrer toute présence d’un pic (un changement positif d’une tension transmembranaire négative à une tension transmembranaire positive), et l’amplitude seuil est définie comme l’amplitude de courant la plus faible qui provoque un pic. Pour ce faire, définissez une procédure appelée findTh() (Supplementary Material-Looping over a range of current amplitudes) à la fin du fichier stimulation.hoc
         2. Enregistrement de la réponse au seuil dans un fichier texte : ajoutez les lignes suivantes à la procédure findTh() dans le fichier stimulation.hoc pour stocker les valeurs de tension transmembranaire calculées pour tous les compartiments neuronaux de chaque pas de temps dans un fichier texte :
            sprint(saveFileName, « Response_%d.dat », th) // Stockez la valeur seuil
            saveFile.wopen(saveFileName)
            for i=0,(responseVector.size()-1){
            saveFile.printf(« %g, « , responseVector.x[i])
            if(i==responseVector.size()-1) {saveFile.printf(« %g\n », responseVector.x[i])
            saveFile.close(saveFileName)
            }}
      2. Automatisation dans le logiciel FEM pour trouver les valeurs de tension pour les neurones à différents endroits
         REMARQUE: Une autre automatisation qui peut être faite est l’acquisition automatique de valeurs de tension extracellulaire pour les neurones à différents endroits. Le menu Application Builder du logiciel FEM permet de définir une « méthode » ou un script pour automatiser les étapes nécessaires à l’exécution des calculs par le logiciel. Pour le démontrer, l’emplacement de la cellule dans la direction x est décalé de 5 fois dans un pas de 100 μm (Figure supplémentaire 6).
         1. Ecrire un code pour les automatisations des simulations FEM.
            1. Accédez à Application Builder, cliquez avec le bouton droit sur Méthodes dans l’arborescence Application Builder, choisissez Nouvelle méthode et cliquez sur OK. Accédez à Préférences > méthodes de > de fichier, cochez la case Afficher tous les codes et cliquez sur OK.
            2. Écrivez un script .hoc qui chargera le fichier de coordonnées, déplacera les valeurs pour qu’elles correspondent à l’emplacement souhaité et enregistrera un fichier texte contenant les valeurs de tension pour le nouvel emplacement de la cellule en tapant les codes affichés dans la méthode Supplementary Material-Defining a pour automatiser les simulations FEM.
         2. Exécution des étapes automatisées dans le logiciel FEM : Basculez vers la méthode Model Builder, Developer > Run > la méthode 1. Cela produira .dat fichiers avec les valeurs de tension appropriées, nommés extracellular_1.dat, extracellular_2.dat, etc.
      3. Mise en boucle des simulations dans un langage de programmation à usage général
         REMARQUE: Pour boucler les simulations, le fichier texte approprié doit être chargé dans la simulation de la suite de calcul neuronale à chaque fois, et un langage de programmation²⁰ qui peut charger et manipuler facilement des fichiers texte est pratique pour effectuer cette étape. N’importe quel environnement de développement intégré (IDE)²¹ pratique peut être utilisé pour cette étape.
         1. Ouvrez l’IDE choisi, cliquez sur Nouveau fichier pour créer un nouveau script. Ici, un fichier .py est utilisé dans cet exemple. Tapez les lignes affichées dans Matériel supplémentaire-Exécution des simulations dans un langage de programmation à usage général.
         2. Enfin, cliquez sur Exécuter ou appuyez sur F5 pour exécuter le script, qui ouvrira également l’interface graphique (Figure 7 supplémentaire).
2. Affichage des données de simulation
   REMARQUE : En suivant toutes les étapes ci-dessus, les résultats de la simulation doivent être stockés dans des fichiers texte, contenant la valeur seuil et le potentiel transmembranaire au seuil. Cependant, l’utilisateur a la possibilité d’afficher le résultat de la simulation pendant que la simulation est en cours d’exécution à l’aide de l’interface graphique de NEURON.
   1. Représenter graphiquement la réponse du modèle neuronal à la stimulation extracellulaire dans l’interface graphique de la suite informatique neuronale. Pour ce faire, exécutez stimulation.hoc, cliquez sur Graph > Voltage Axis dans la barre d’outils, et dans la fenêtre du graphique, cliquez avec le bouton droit de la souris n’importe où et choisissez Tracer quoi.
   2. Tapez 'axon.v(1)' dans le champ Variable to Graph , ce qui signifie qu’il tracera le potentiel transmembranaire du dernier segment de l’axone par pas de temps.

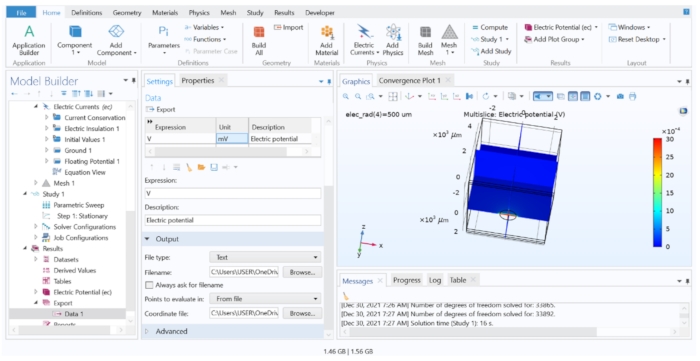
Figure 7 : Affichage et exportation des résultats de calcul FEM dans un fichier texte. La fenêtre graphique montrant un tracé multitranche du potentiel électrique dans V. Les options du paramètre d’exportation de données permettaient d’exporter la variable calculée dans un fichier texte. Veuillez cliquer ici pour voir une version agrandie de cette figure.

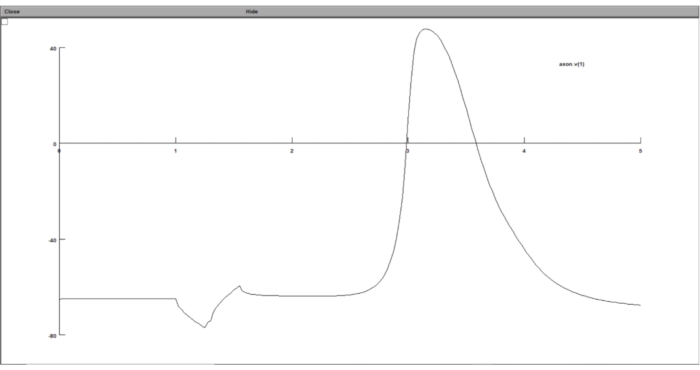
Figure 8 : Affichage du graphique du potentiel transmembranaire à l’aide d’un graphique de tension. Le potentiel transmembranaire neuronal a été affiché dans l’interface graphique de la suite informatique neuronale. L’axe des x est le temps en ms, tandis que l’axe des y est le potentiel transmembranaire du segment neuronal choisi en mV. Veuillez cliquer ici pour voir une version agrandie de cette figure.

Résultats

Nous avons mené deux protocoles de simulation pour démontrer l’utilisation du modèle. Le premier protocole consistait à faire varier la taille de l’électrode tout en conservant l’emplacement du neurone et les paramètres de l’impulsion électrique. Le deuxième protocole consistait à déplacer le neurone dans la direction x par pas de 100 μm, tandis que la taille de l’électrode restait constante. Pour les deux protocoles, l’impulsion utilisée était une impulsion biphasique cathodique unique de 0,25 ...

Discussion

Dans cet article, nous avons démontré un flux de travail de modélisation qui combinait la modélisation par éléments finis et la modélisation des neurones biophysiques. Le modèle est très flexible, car sa complexité peut être modifiée pour s’adapter à différents objectifs, et il fournit un moyen de valider les résultats par rapport aux résultats empiriques. Nous avons également démontré comment nous avons paramétré le modèle pour permettre l’automatisation.

La méthode...

matériels

Name	Company	Catalog Number	Comments
Computer workstation	N/A	N/A	Windows 64-bit operating system, at least 4GB of RAM, at least 3 GB of disk space
Anaconda Python	Anaconda Inc.	Version 3.9	The open source Individual Edition containing Python 3.9 and preinstalled packages to perform data manipulation, as well as Spyder Integrated Development Environment. It could be used to control the simulation, as well as to display and analyse the simulation data.
COMSOL Multiphysics	COMSOL	Version 5.6	The simulation suite to perform finite element modelling. The licence for the AC/DC module should be purchased. The Application Builder capability should be included in the licence to follow the automation tutorial.
NEURON	NEURON	Version 8.0	A freely-distributed software to perform the computation of neuronal cells and/or neural networks.