Modelagem Computacional de Neurônios da Retina para Pesquisa de Próteses Visuais - Abordagens Fundamentais

Resumo

Resumimos um fluxo de trabalho para modelar computacionalmente os comportamentos de um neurônio da retina em resposta à estimulação elétrica. O modelo computacional é versátil e inclui etapas de automação que são úteis na simulação de uma variedade de cenários fisiológicos e na antecipação dos resultados de futuros estudos in vivo / in vitro .

Resumo

A modelagem computacional tem se tornado um método cada vez mais importante na engenharia neural devido à sua capacidade de prever comportamentos de sistemas in vivo e in vitro . Isso tem a principal vantagem de minimizar o número de animais necessários em um determinado estudo, fornecendo uma previsão muitas vezes muito precisa dos resultados fisiológicos. No campo da prótese visual, a modelagem computacional tem uma série de aplicações práticas, incluindo informar o projeto de uma matriz de eletrodos implantáveis e prever percepções visuais que podem ser provocadas através da entrega de impulsos elétricos da referida matriz. Alguns modelos descritos na literatura combinam uma morfologia tridimensional (3D) para calcular o campo elétrico e um modelo de cabo do neurônio ou rede neural de interesse. Para aumentar a acessibilidade deste método de duas etapas para pesquisadores que podem ter experiência anterior limitada em modelagem computacional, fornecemos um vídeo das abordagens fundamentais a serem tomadas para construir um modelo computacional e utilizá-lo na previsão dos resultados fisiológicos e psicofísicos de protocolos de estimulação implantados via uma prótese visual. O guia compreende as etapas para a construção de um modelo 3D em um software de modelagem de elementos finitos (MEF), a construção de um modelo de células ganglionares da retina em um software computacional de neurônios multicompartimentais, seguido pela fusão dos dois. Um software de modelagem de elementos finitos para resolver numericamente equações físicas seria usado para resolver a distribuição do campo elétrico nas estimulações elétricas do tecido. Em seguida, foi utilizado um software especializado para simular as atividades elétricas de uma célula ou rede neural. Para seguir este tutorial, a familiaridade com o princípio de funcionamento de uma neuroprótese, bem como conceitos neurofisiológicos (por exemplo, mecanismo de potencial de ação e uma compreensão do modelo de Hodgkin-Huxley), seria necessária.

Introdução

As neuropróteses visuais são um grupo de dispositivos que fornecem estímulos (elétricos, leves, etc.) às células neurais na via visual para criar fosfénos ou sensação de ver a luz. É uma estratégia de tratamento que está em uso clínico há quase uma década para pessoas com cegueira permanente causada por doenças degenerativas da retina. Normalmente, um sistema completo incluiria uma câmera externa que captura as informações visuais em torno do usuário, uma fonte de alimentação e uma unidade de computação para processar e traduzir a imagem para uma série de pulsos elétricos e uma matriz de eletrodos implantados que interage com o tecido neural e entrega os pulsos elétricos às células neurais. O princípio de funcionamento permite que uma neuroprótese visual seja colocada em diferentes locais ao longo da via visual da retina ao córtex visual, desde que esteja a jusante do tecido danificado. A maioria das pesquisas atuais em neuropróteses visuais se concentra em aumentar a eficácia da estimulação e melhorar a acuidade espacial para fornecer uma visão mais natural.

Nos esforços para melhorar a eficácia da estimulação, a modelagem computacional tem sido um método econômico e eficaz em termos de tempo para validar o projeto de uma prótese e simular seu resultado visual. A modelagem computacional neste campo ganhou popularidade desde 1999, quando Greenberg¹ modelou a resposta de uma célula ganglionar da retina a estímulos elétricos extracelulares. Desde então, a modelagem computacional tem sido utilizada para otimizar os parâmetros do pulso elétrico^2,3 ou o desenho geométrico do eletrodo ^4,5. Apesar da variação na complexidade e nas questões de pesquisa, esses modelos funcionam determinando a distribuição de tensão elétrica no meio (por exemplo, tecido neural) e estimando a resposta elétrica que os neurônios nas proximidades produzirão devido à tensão elétrica.

A distribuição de tensão elétrica em um condutor pode ser encontrada resolvendo as equações de Poisson⁶ em todos os locais:

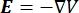
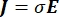
onde E é o campo elétrico, V o potencial elétrico, J a densidade de corrente e σ é a condutividade elétrica. O 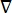na equação indica um operador de gradiente. No caso da corrente estacionária, as seguintes condições de contorno são impostas ao modelo:

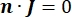
onde n é o normal para a superfície, Ω representa o limite e I₀ representa a corrente específica. Juntos, eles criam isolamento elétrico nos limites externos e criam uma fonte de corrente para um limite selecionado. Se assumirmos uma fonte pontual monopolar em um meio homogêneo com uma condutividade isotrópica, o potencial elétrico extracelular em um local arbitrário pode ser calculado por⁷:

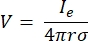
onde I e é a corrente e é a distância entre o eletrodo _e o ponto de medição. Quando o meio é não homogêneo ou anisotrópico, ou a matriz de eletrodos tem múltiplos eletrodos, um conjunto computacional para resolver numericamente as equações pode ser conveniente. Um software de modelagem de elementos finitos⁶ divide o condutor de volume em pequenas seções conhecidas como "elementos". Os elementos estão interligados uns com os outros de tal forma que os efeitos da mudança em um elemento influenciam a mudança em outros, e resolve as equações físicas que servem para descrever esses elementos. Com o aumento da velocidade computacional dos computadores modernos, esse processo pode ser concluído em segundos. Uma vez que o potencial elétrico é calculado, pode-se então estimar a resposta elétrica do neurônio.

Um neurônio envia e recebe informações na forma de sinais elétricos. Tais sinais vêm em duas formas - potenciais graduais e potenciais de ação. Potenciais graduais são mudanças temporárias no potencial de membrana em que a tensão através da membrana se torna mais positiva (despolarização) ou negativa (hiperpolarização). Potenciais graduados, normalmente, têm efeitos localizados. Nas células que os produzem, os potenciais de ação são respostas de tudo ou nada que podem viajar longas distâncias ao longo do comprimento de um axônio. Ambos os potenciais graduados e de ação são sensíveis ao ambiente elétrico e químico. Um pico de potencial de ação pode ser produzido por vários tipos de células neuronais, incluindo as células ganglionares da retina, quando um potencial transmembrana limiar é cruzado. O potencial de ação e propagação desencadeia a transmissão sináptica de sinais para os neurônios a jusante. Um neurônio pode ser modelado como um cabo que é dividido em segmentos cilíndricos, onde cada segmento possui capacitância e resistência devido à membrana de bicamada lipídica⁸. Um programa computacional de neurônios⁹ pode estimar a atividade elétrica de uma célula eletricamente excitável discretizando a célula em múltiplos compartimentos e resolvendo o modelo matemático¹⁰:

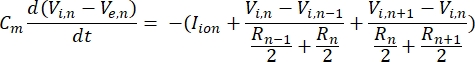
Nesta equação, C_mé a capacitância da membrana, V e,n é o potencial extracelular no nó n, V_i,n o potencial intracelular no nó n, R n a resistência intracelular (longitudinal) no nó n e o_íon I é a corrente iônica que atravessa os canais iônicos no nó _n. Os valores de V do modelo FEM são implementados como V_e,n para todos os nós do neurônio quando a estimulação está ativa.

As correntes transmembranares dos canais iônicos podem ser modeladas usando formulações de Hodgkin-Huxley¹¹:

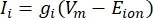
onde g i é a condutância específica do canal, V _m o potencial transmembrana (V _i,n - V_e,n) _{e E íon} o potencial de reversão do canal iônico. Para canais dependentes de tensão, como o canal Na, são introduzidos parâmetros adimensionais, m e h, que descrevem a probabilidade de abertura ou fechamento dos canais:

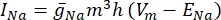
onde 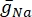é a condutância máxima da membrana para o canal iônico particular, e os valores dos parâmetros m e h são definidos por equações diferenciais:

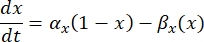
onde α x e β_x são funções dependentes de tensão que definem as constantes de taxa do canal iônico. Eles geralmente assumem a forma:

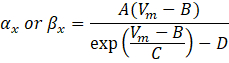
Os valores dos parâmetros nessas equações, incluindo a condutância máxima, bem como as constantes A, B, C e D, foram tipicamente encontrados a partir de medições empíricas.

Com esses blocos de construção, modelos de diferentes complexidades podem ser construídos seguindo as etapas descritas. Um software FEM é útil quando a equação de Poisson não pode ser resolvida analiticamente, como no caso de condutância não homogênea ou anisotrópica no condutor de volume ou quando a geometria da matriz de eletrodos é complexa. Depois que os valores de potencial extracelular foram resolvidos, o modelo de cabo de neurônios pode então ser resolvido numericamente no software computacional de neurônios. A combinação dos dois softwares permite a computação de uma célula ou rede de neurônios complexos para um campo elétrico não uniforme.

Um modelo simples de duas etapas de uma célula ganglionar da retina sob uma estimulação supracoroidal será construído usando os programas acima mencionados. Neste estudo, a célula ganglionar da retina será submetida a uma gama de magnitudes de pulsos de corrente elétrica. A localização da célula em relação ao estímulo também é variada para mostrar a relação distância-limiar. Além disso, o estudo inclui uma validação do resultado computacional em relação a um estudo in vivo do limiar de ativação cortical usando diferentes tamanhos de eletrodo de estimulação¹², bem como um estudo in vitro mostrando a relação entre a distância eletrodo-neurônio e o limiar de ativação¹³.

Protocolo

1. Configurando o modelo de elementos finitos para cálculos de potencial elétrico

1. Determinar as etapas de simulação e a complexidade do modelo
   NOTA: O objetivo da primeira etapa é esclarecer o propósito da modelagem, que determinará os elementos necessários do modelo e do procedimento de simulação. Um ponto importante a considerar é o comportamento das células neurais que precisa ser mostrado pelo modelo e qual protocolo de teste seria necessário para demonstrar esse comportamento. Este estudo mostra uma relação distância-limiar para um neurônio que é estimulado extracelularmente, bem como a curva tamanho-limiar do eletrodo. Para fazer isso, é necessário um modelo de células neurais compartimentado em diferentes seções (para incorporar a variação de parâmetros morfológicos e biofísicos no neurônio) sensíveis à tensão extracelular e simulação de uma variedade de tamanhos e posições de eletrodos.
   1. Definir a questão de pesquisa e as variáveis experimentais.
      1. Definir uma questão de pesquisa e um protocolo de teste para orientar a construção do modelo. É melhor começar com uma pergunta clara e construir um modelo o mais simples possível para respondê-la.
   2. Determinar os elementos necessários a serem incluídos no modelo completo
      NOTA: Nesta abordagem de modelagem, a célula é vista como sendo imersa em um meio eletricamente condutor, isto é, o tecido biológico. A estimulação elétrica acontece através deste "condutor de volume", ou seja, o meio, resultando em uma distribuição do potencial elétrico.
      1. Com base nas questões de pesquisa e variáveis a serem resolvidas, decida se ambos os elementos (FEM e modelo de cabo de neurônios) são necessários. Se, por exemplo, a modelagem precisar de um único eletrodo que possa ser simplificado como fonte pontual e que o meio seja homogêneo, um FEM pode não ser necessário, e um cálculo analítico do campo elétrico extracelular pode ser feito para substituí-lo.
2. Baixe e instale o software
   NOTA: O estudo utilizou as versões de aplicativos de software (COMSOL, NEURON e Python Anaconda) e hardware especificado na Tabela de Materiais. Pode haver pequenas diferenças nas etapas ou nos resultados se forem usadas versões diferentes do software/hardware.
   1. Baixe o software adequado ao sistema operacional do computador e adquira uma licença, se necessário. Certifique-se de que todos os módulos de simulação necessários são baixados e instale todo o software.
3. Reunir os dados sobre a anatomia do tecido e da célula a serem modelados
   NOTA: Para este método, os parâmetros anatômicos e biofísicos foram retirados dos achados empíricos. É comum que modelos computacionais misturem parâmetros medidos em diferentes espécies devido à indisponibilidade de dados. Para uma simulação de estimulação supracoroidal, as camadas de tecido entre os eletrodos estimulantes e de referência precisam ser incluídas no modelo.
   1. Reúna a anatomia do tecido a partir de estudos histológicos.
      1. Neste modelo, incluem a coroide, o tecido retiniano e os domínios vítreos, onde cada domínio é modelado como um prisma retangular para facilitar a construção do modelo. Coletar a espessura média do tecido retiniano a partir de dados histológicos publicados¹⁴ para posteriormente ser usado como a altura de cada prisma.
   2. Colete os dados de morfologia de célula única da coloração celular ou do banco de dados público de neurônios.
      1. Baixe a morfologia detalhada do neurônio de um banco de dados como o NeuroMorpho.org, que fornece um recurso de Metadados de Pesquisa para encontrar o neurônio relevante com base na espécie, região do cérebro, tipo de célula, etc. Para este estudo, encontre o modelo OFF RGC de Guo (D23WM13_27_1-OffRGC_msa)¹⁵ inserindo Coelho > Nova Zelândia Branca no campo Espécie e Retina no campo Região Cerebral . Clique no modelo e baixe o arquivo .swc.
4. Reunir os dados biofísicos da célula modelada
   NOTA: Os parâmetros biofísicos incluem os valores de condutividade elétrica para cada camada de tecido e os parâmetros elétricos da membrana neural e dos canais iônicos.
   1. Devido à disponibilidade de dados, utilizar os valores de condutividade elétrica que foram retirados do coelho¹⁶ para o modelo tecidual, enquanto a dinâmica dos canais iônicos foi baseada no modelo de Sheasby e Fohlmeister da retina da salamandra-tigre¹⁷.
5. Construir a geometria do modelo de elementos finitos do tecido e eletrodo no software FEM
   NOTA: A geometria do tecido e da matriz de eletrodos afeta a distribuição do potencial elétrico, que por sua vez influencia o comportamento das células neurais. Portanto, a construção de uma geometria realista do meio onde as células residem, bem como o eletrodo, é importante. O software FEM usado neste tutorial tem uma GUI que permite a fácil construção da geometria do modelo.
   1. Configurando o modelo FEM na GUI do software:
      1. Execute o software FEM e clique em Assistente de Modelo > 3D. Na caixa de listagem Selecionar Física, expanda o AC/DC > Campos Elétricos e Corrente > Correntes Elétricas (ec) e clique em Adicionar. Clique em Estudo e adicione um Estudo Estacionário na opção Estudos Gerais e, em seguida, clique em Concluído (Figura Suplementar 1).
   2. Configuração da unidade e dos parâmetros geométricos do eletrodo.
      1. Na árvore do Construtor de Modelos, clique em Parâmetros 1. Na tabela, digite 'elec_rad' no campo Nome e '50' no campo Expressão para criar um eletrodo com 50 unidades de raio. Em seguida, clique em Geometria e altere a unidade de Comprimento para μm, pois a soma de uma célula ganglionar típica da retina tem cerca de 10 μm de diâmetro (Figura 2 Suplementar).
   3. Criar as camadas de tecido usando domínios de bloco
      NOTA: Para a construção da geometria do modelo, foram utilizados três blocos para representar diferentes estruturas no olho. O bloco 1 representava a coroide, o bloco 2 o tecido retiniano e o bloco 3 o vítreo.
      1. Clique com o botão direito do mouse em Geometria 1 > Bloco para criar um domínio de bloco. Repita esta etapa mais duas vezes para criar três blocos no total. Para todos os blocos, defina Profundidade e Largura como 5.000 μm e altere a opção Base (em Posição) para Centro. Atribua os seguintes valores de Altura (em Tamanho e Forma) e z (em Posição) para cada bloco:
         Bloco 1: Altura = 112 μm, z = 0 μm
         Bloco 2: Altura = 151 μm, z = 131,5 μm
         Bloco 3: Altura = 5.000 μm, z = 2.707 μm
   4. Criando um plano de trabalho para adicionar um eletrodo ao modelo
      1. Clique com o botão direito do mouse na Geometria 1 na Árvore Modelo e escolha Plano de Trabalho. Clique em Plano de Trabalho 1 e altere o Tipo de Plano para Face Paralela, clique no botão Ativar Seleção abaixo do Tipo de Plano e escolha a superfície inferior do Bloco 1 (blk 1 > 1).
   5. Desenhando um eletrodo de disco no plano de trabalho
      1. Clique em Geometria do Plano em Plano de Trabalho 1 e clique em Esboço na barra de ferramentas principal. Selecione Círculo, clique em qualquer lugar dentro do retângulo na guia Gráficos e arraste para criar um eletrodo de disco. Altere o raio para 'elec_rad' μm, xw e yw para 0 μm e, em seguida, clique em Build All.
   6. Atribuindo propriedades de material a cada domínio
      NOTA: Seguindo as etapas para construir a geometria, o modelo seria separado em vários 'domínios', que são partes 3D individuais que compõem a geometria completa. A cada domínio deve ser atribuído um valor de condutividade elétrica para calcular a distribuição do campo elétrico em todo o modelo.
      1. Na Árvore Modelo, clique com o botão direito do mouse em Material > Material em Branco e, em seguida, clique em Material 1 e altere a Seleção para Manual.
      2. Clique nos domínios na janela Gráficos para que apenas o domínio 1 seja escolhido. Escolha Propriedades do Material > Propriedades Básicas > Condutividade Elétrica, clique no botão Adicionar ao Material e altere o valor de Condutividade Elétrica para o valor para 0,043 S/m¹⁵.
      3. Repita as etapas para os domínios 2 e 3, com os valores de condutividade elétrica de 0,7 16 e 1,55¹⁶ S/m, respectivamente (Figura suplementar 3).
   7. Mesclando um modelo 3D: Para mesclar o modelo, vá para a Árvore Modelo e clique com o botão direito do mouse em Malha 1 > Tetraédrico Livre. Clique em Free Tetrahedral 1 e escolha Build All.
      NOTA: O processo de malha divide toda a geometria em "elementos" menores (um elemento é um segmento virtual da geometria do modelo onde as equações físicas são resolvidas numericamente). A malha com elementos menores teoricamente aumenta a precisão da aproximação, mas é computacionalmente exaustiva. Uma prática comum é iniciar o modelo com malha esparsa e registrar o resultado da simulação, repetindo continuamente a simulação com elementos de malha menores a cada vez e comparando os resultados. O processo de refinamento pode parar quando não há diferença significativa nos resultados do cálculo das etapas de refinamento subsequentes.
      1. Avaliando a qualidade da malha: clique com o botão direito do mouse em Malha 1 e escolha Estatísticas para mostrar o histograma da qualidade do elemento. Siga as etapas de refinamento de malha abaixo para melhorar a qualidade dos elementos.
         Observação : usando a malha padrão pode produzir muitos elementos de baixa qualidade, que por sua vez torna cálculos imprecisos. Na maioria dos casos, é necessário algum grau de refinamento da malha.
      2. Refinando a malha ao redor do perímetro do eletrodo
         NOTA: As áreas onde pode haver mudanças abruptas no campo elétrico normalmente exigem uma malha mais refinada. Aqui, uma malha mais densa ao redor do perímetro do eletrodo foi adicionada usando o recurso de distribuição de bordas.
         1. Em primeiro lugar, elimine a malha Tetraédrica Livre 1 existente. Em seguida, clique com o botão direito do mouse em Malha 1 > Distribuição, clique em Distribuição 1, altere o Nível de Entidade Geométrica para Borda e escolha Bordas 19-22 (o perímetro do eletrodo de disco).
         2. Defina o Tipo de Distribuição como Número Fixo de Elementos e altere o campo Número de Elementos para elec_rad*3/10 para tornar os elementos razoavelmente pequenos.
      3. Refinando a malha através da coroide e do tecido da retina
         1. Na Árvore Modelo, clique com o botão direito do mouse em Malha 1 > Varrido. Clique em Varrido 1. Escolha Domínios 1 e 2. Em seguida, clique com o botão direito do mouse em Malha 1 > Tetraédrico Livre, defina o Nível de Entidade Geométrica como Restante e clique em Construir Tudo. (Opcional: Verifique o histograma de qualidade do elemento novamente para garantir que os elementos de baixa qualidade tenham sido reduzidos em proporção).
6. Aplicar a física ao modelo de elementos finitos
   NOTA: A "física" no software FEM são conjuntos de equações matemáticas e condições de contorno que precisam ser atribuídas ao modelo. É o cálculo da solução para o conjunto simultâneo de equações que é realizado durante o curso da execução do modelo. A escolha da física a aplicar à geometria depende do fenômeno físico que é simulado. Por exemplo, a física da corrente elétrica, como usada neste modelo, observa a distribuição do campo elétrico e negligencia o fenômeno magnético (indutivo). Outra física poderia ser aplicada à geometria se outros problemas físicos (por exemplo, distribuição de temperatura, tensão mecânica, etc.) fossem resolvidos.
   1. Seleção da física e aplicação das condições de contorno
      NOTA: Se um pulso de tensão constante deve ser aplicado, a condição de limite do potencial flutuante deve ser substituída por uma condição de limite do potencial elétrico.
      1. Expanda Correntes Elétricas 1 na Árvore Modelo e verifique se a Conservação de Corrente 1, o Isolamento Elétrico 1 e os Valores Iniciais 1 estão listados. Em seguida, clique com o botão direito do mouse nas Correntes Elétricas 1 > Aterramento (isso atribui 0 V a um plano distante, simulando um eletrodo de referência distante) e aplique-o à superfície mais distante do eletrodo (Superfície 10).
      2. Em seguida, clique com o botão direito do mouse nas Correntes Elétricas 1 > Potencial Flutuante (isso simula uma fonte de corrente com corrente constante), atribuído ao eletrodo de disco (superfície 14), e altere o valor I ₀ para 1[μA] para aplicar uma corrente unitária.
   2. Executando a simulação com uma varredura paramétrica.
      NOTA: Esta etapa executará a simulação e uma varredura paramétrica foi adicionada, onde várias simulações foram feitas com o valor de um parâmetro alterado em cada simulação. Aqui, o parâmetro de raio do eletrodo foi varrido e a distribuição do potencial elétrico para cada simulação foi armazenada no arquivo do modelo. Após a execução da simulação, o ramo Resultados na Árvore Modelo foi preenchido com um gráfico Multislice de Potencial Elétrico (ec).
      1. Na Árvore Modelo, clique com o botão direito do mouse no Estudo 1 > Varredura Paramétrica. Clique em Varredura Paramétrica e, na tabela Configuração do Estudo , clique em Adicionar e escolha elec_rad para o Nome do Parâmetro.
      2. Digite '50, 150, 350, 500' para a Lista de Valores de Parâmetros e 'μm' para a Unidade de Parâmetros, e clique em Computar para executar o estudo (Figura 4 Suplementar).

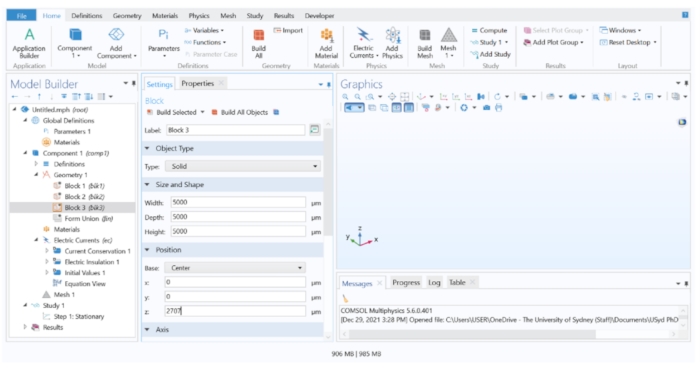
Figura 1: Criando a geometria do tisssue. Uma geometria de bloco foi inserida no modelo FEM para representar o tecido. Por favor, clique aqui para ver uma versão maior desta figura.

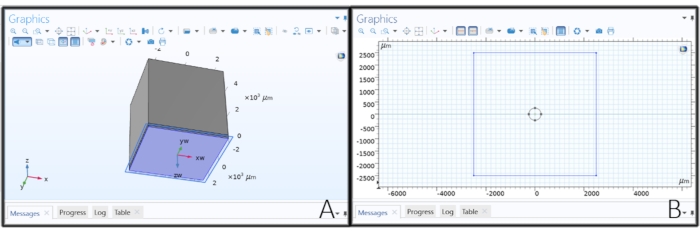
Figura 2: Criando a geometria do eletrodo. (A) Fazendo um plano de trabalho para desenhar o eletrodo de disco. (B) Esboçar um círculo em um plano de trabalho para criar um eletrodo de disco. Por favor, clique aqui para ver uma versão maior desta figura.

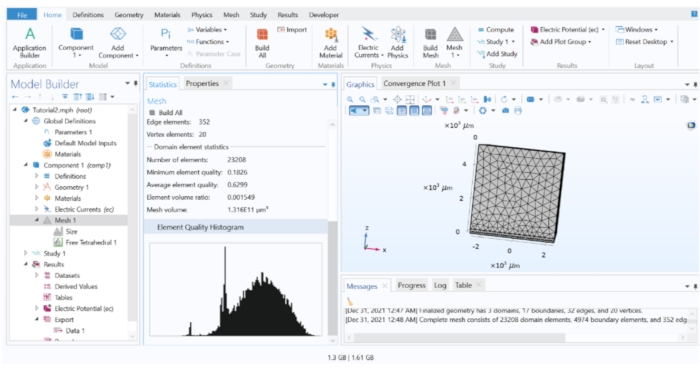
Figura 3: O histograma de qualidade do elemento do modelo FEM. O histograma mostrou a qualidade dos elementos em todo o modelo. Refinamentos de malha são necessários se uma parte significativa dos elementos estiver na região de baixa qualidade. Por favor, clique aqui para ver uma versão maior desta figura.

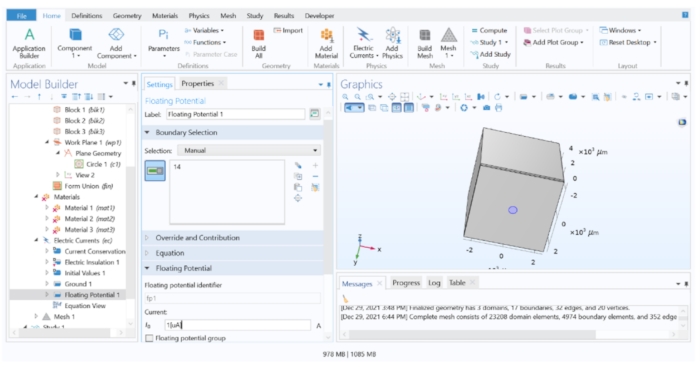
Figura 4: Atribuindo um valor de corrente ao eletrodo. Uma corrente unitária aplicada à geometria do eletrodo no software FEM. Por favor, clique aqui para ver uma versão maior desta figura.

2. Importando a geometria da célula neural na GUI do conjunto computacional de neurônios

1. Criar a geometria do modelo de célula
   1. Importando a morfologia usando o recurso Construtor de Células.
      1. Execute 'nrngui' a partir da pasta de instalação do neuron computational suite, clique em Ferramentas > Miscellaneous > Import 3D e, em seguida, marque a caixa Escolher um arquivo .
      2. Localize o arquivo .swc baixado e clique em Ler. Depois que a geometria for importada, clique em Exportar > Cell Builder (Figura 5 Suplementar).
   2. Criando um arquivo .hoc da morfologia da célula importada
      1. Vá para a guia Subconjuntos e observe os subconjuntos que foram predefinidos no modelo (por exemplo, soma, axônio, basal, etc.). Marque a caixa Criação Contínua , vá para Gerenciamento > Exportar e exporte a morfologia como 'rgc.hoc'.
   3. Visualizando a morfologia da célula
      1. Clique em Ferramenta > Model View > 1 Real Cells > Root Soma[0] na barra de ferramentas, clique com o botão direito do mouse na janela que aparece e clique em Axis Type > View Axis. Por inspeção visual, o diâmetro do campo dendrítico deste modelo é de cerca de 250 μm. Feche as janelas NEURON por enquanto.

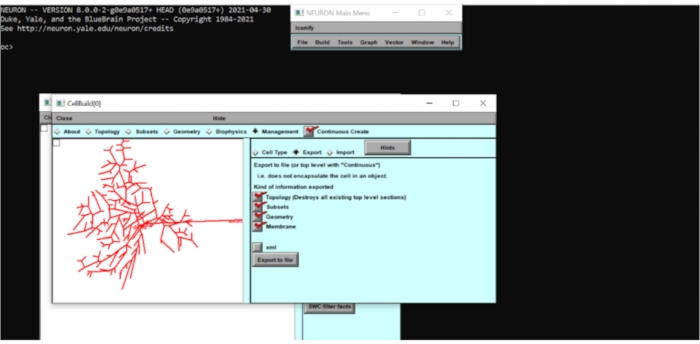
Figura 5: Exportando as informações do modelo de neurônios como um arquivo .hoc. A geometria do neurônio foi exportada para um arquivo .hoc para permitir modificações adicionais. Por favor, clique aqui para ver uma versão maior desta figura.

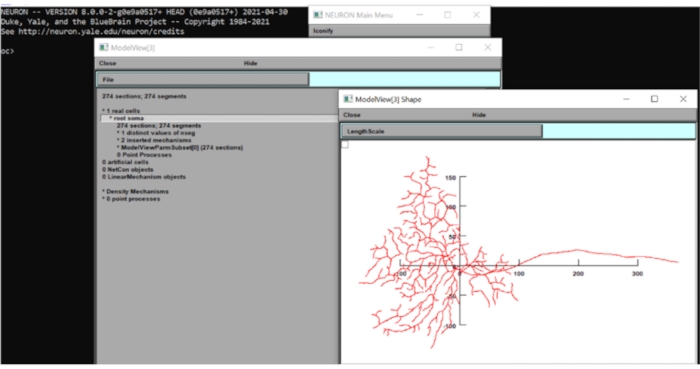
Figura 6: Medindo a dimensão do neurônio. A morfologia do neurônio (vista superior) foi exibida na GUI do conjunto computacional de neurônios com os eixos x-y sobrepostos. A escala estava em μm. Clique aqui para ver uma versão maior desta figura.

3. Programando a simulação computacional NEURON

1. Ajustando a morfologia da célula programando em linguagem .hoc
   NOTA: A morfologia da célula pode ser ajustada através do recurso Cell Builder da GUI. No entanto, como isso poderia ser feito editando o arquivo .hoc para acelerar o processo é demonstrado. O arquivo .hoc define a topologia (conexões físicas entre cada parte dos neurônios), morfologia (o comprimento, diâmetro e localização de cada seção de neurônios) e as propriedades biofísicas (parâmetros de canal iônico) da célula modelada. A documentação completa para programação .hoc pode ser encontrada em: https://neuron.yale.edu/neuron/static/new_doc/index.html#,
   1. Abra o arquivo .hoc resultante com um editor de texto (por exemplo, Bloco de Notas). Adicione um segmento inicial axônico de 40 μm de comprimento e um segmento axonal estreito de 90 μm de comprimento próximo ao soma, conforme descrito em Sheasby e Fohlmeister¹⁷, bem como altere o comprimento dos dendritos para que o tamanho do campo dendrítico se torne 180 μm para corresponder à célula G1 em Rockhill, et ^al.18.
      1. Criando novas seções de célula e definindo as conexões topológicas para cada seção.
         1. Para criar novas seções de célula para o segmento inicial do axônio (AIS) e o segmento axonal estreito (NS), adicione estas linhas ao início do arquivo rgc.hoc:
            criar AIS, NS // Declarando compartimentos celulares chamados AIS e NS
            Em seguida, substitua a linha 'conectar axônio(0), soma[1](1)' por:
            conectar ais(0), soma[1](1) // Conectando o primeiro segmento do AIS ao final do soma[1]
            connect ns(0), ais(1) // Conectando o primeiro segmento do NS ao final do AIS
            conectar axônio(0), ns(1) // Conectando o primeiro segmento do axônio ao final do NS
      2. Definindo as posições, diâmetros e comprimento 3D das seções de células
         1. Defina as posições e diâmetros 3D dos compartimentos AIS e NS escrevendo estas linhas dentro dos colchetes 'proc shape3d_31()':
            ais { pt3dadd(-2.25, -1.55, 0, 1) // Os três primeiros números são a coordenada xyz, e o diâmetro é de 1 μm
            pt3dadd(37,75, -1,55, 0, 1)} // O primeiro ponto está em x = -2,25 μm e o último ponto está em x = 37,75 μm
            ns { pt3dadd(37.75, -1.55, 0, 0.3) // As coordenadas 3D e o diâmetro para os segmentos NS
            pt3dadd(127,75, -1,55, 0, 0,3)}
         2. No final do arquivo, desloque a coordenada 3D do axônio para que seu ponto inicial atenda ao ponto final do NS digitando:
            axon {for i=0,n3d()-1 {pt3dchange(i, x3d(i)+130, y3d(i),z3d(i)-5, diam3d(i))}} //Shift a coordenada x
         3. No final do arquivo, encurte os compartimentos dendríticos em 18% digitando:
            forsec basal {L=L*0,82} // Dimensionamento do comprimento para tornar o tamanho do campo dendrítico menor
            define_shape() // Preenchimento de informações 3D em falta
2. Definindo o número de segmentos para cada seção
   NOTA: Cada seção do neurônio pode ser espacialmente discreta, muito parecido com o processo de malha no modelo FEM. A discretização espacial divide o neurônio virtualmente em segmentos menores, onde os cálculos devem ser feitos. Para o número de segmentos 'nseg', certifique-se de que números ímpares sejam usados para garantir que haja um nó interno no ponto médio de uma seção de célula e tente triplicar o número nseg até que a computação produza um resultado consistente⁹. Um número maior de segmentos produzirá uma aproximação numérica mais precisa, mas também aumentará a carga computacional.
   1. Para exemplificar o processo de discretização, adicione as seguintes linhas no arquivo rgc.hoc para dividir as seções neuronais nos subconjuntos somático e axonal em vários segmentos:
      forsec somático {nseg=31}
      forsec axonal {nseg=301}
      Outras seções no modelo também precisam ser discretizadas digitando essas linhas, mas alterando o nome do subconjunto (após 'forsec') e o número de segmentos (após 'nseg') conforme desejado.
3. Inserir mecanismos de canal iônico personalizados
   1. Escrevendo mecanismos de canal iônico personalizados como arquivos .mod: Para aplicar os mecanismos de canal iônico, crie arquivos .mod e insira os arquivos na parte da seção biofísica do arquivo .hoc seguindo as etapas 3.3.1-3.3.3. O arquivo .mod contém as variáveis e as equações diferenciais a serem resolvidas para cada canal iônico.
      NOTA: As definições e implementações corretas do mecanismo de canal iônico são críticas em simulações precisas de neurônios. Ao escrever arquivos .mod, verifique se as unidades estão corretas (o utilitário 'modlunit' fornecido que pode ser executado para verificar a consistência da unidade) e se as equações estão escritas corretamente. Para testar se os mecanismos dos canais iônicos estão corretos, a corrente para cada canal iônico durante a estimulação intracelular ou extracelular pode ser plotada e comparada aos achados empíricos.
      1. Canais iônicos dependentes de tensão
         NOTA: Um arquivo .mod para criar um canal iônico dependente de tensão normalmente inclui um bloco DERIVATIVE que tem a equação diferencial a ser resolvida, um bloco BREAKPOINT que tem os comandos para resolver as equações diferenciais usando um método de aproximação numérica escolhido e blocos PROCEDURE que instruem o programa a calcular os parâmetros de bloqueio (por exemplo, mt, ht e d neste exemplo). Este código calculará os valores da corrente iônica que passa pelo canal para cada etapa de tempo.
         1. Para exemplificar o processo, crie um canal Ca dependente de tensão que tenha equações diferenciais de primeira ordem para resolver as variáveis de bloqueio.
         2. Abra um novo arquivo no editor de texto e digite as linhas no canal Cat Suplementar Material-Defining a voltage-dependente. Salve esse arquivo como Cat.mod na mesma pasta que o arquivo .hoc. Esse processo precisa ser repetido para os outros canais iônicos que o neurônio modelo contém.
      2. Canais iônicos dependentes de tensão e concentração
         1. A cinética de alguns canais iônicos, como os canais de potássio ativados por cálcio nas células ganglionares da retina, depende da concentração intracelular de cálcio, além da voltagem transmembrana¹⁹. Para modelar esse tipo de mecanismo, crie um arquivo chamado KCa.mod e digite as linhas conforme mostrado em Canais iônicos dependentes de tensão e concentração de material suplementar. Neste arquivo .mod, a variável 'cai', que é definida como a concentração interna do íon Ca foi calculada, e então essa variável é usada na equação para calcular a corrente iKCa.
   2. Compilação de arquivos .mod
      1. Compile todos os arquivos .mod executando o utilitário mknrndll da suíte computacional neuron a partir da pasta de instalação. Localize a pasta onde os arquivos .mod estão contidos e clique em compilar para criar arquivos O e C. Depois disso, os mecanismos podem ser inseridos neste modelo celular.
   3. Aplicação dos arquivos .mod no arquivo de modelo NEURON principal.
      NOTA: Além de inserir os canais iônicos, a condutância máxima de Na foi definida apenas para o subconjunto 'somático'. Poderíamos ajustar individualmente a condutância máxima da membrana para diferentes segmentos neuronais, se necessário.
      1. Para maior brevidade, combine todos os mecanismos de canal iônico em um único arquivo .mod (arquivo .mod Supplementary Material-Complete). Insira o arquivo .mod combinado contendo todos os canais iônicos e um canal de vazamento passivo em todos os segmentos do subconjunto 'somático' digitando as linhas abaixo no procedimento 'biophys' do arquivo rgc.hoc:
         forsec somatic {insert rgcSpike
         inserir pas // canal de fuga passivo
         gnabar_rgcSpike = 80e-3
         g_pas = 0,008e-3 // condutância da membrana de vazamento}
   4. Definindo a resistividade axoplasmática
      1. As células têm resistividade axoplasmática que pode ser alterada por compartimento. Para este modelo, todos os segmentos têm a mesma resistividade de 110 Ω·cm. Altere a resistividade axoplasmática no arquivo rgc.hoc:
         forall {Ra = 110}
4. Inserir mecanismos extracelulares e definir a forma de onda do pulso
   1. Inserindo um mecanismo extracelular no modelo celular
      1. Para que o modelo de célula responda à tensão extracelular, insira um mecanismo extracelular em todos os segmentos digitando a linha na parte inferior do arquivo rgc.hoc:
         forall {inserir extracelular}
   2. Criando um pulso bifásico
      Observação : nesta demonstração, um pulso bifásico de corrente constante é feito que é ajustável pelo usuário em largura de pulso, intervalo entre fases e o número de repetições criando um procedimento em um arquivo .hoc. Para um programa mais estruturado, use o arquivo rgc.hoc como um arquivo para criar o modelo de célula, enquanto o processo de estimulação é aplicado em um arquivo .hoc separado, que carregaria o modelo de célula ao qual a estimulação é aplicada.
      1. Crie um novo arquivo de texto chamado stimulation.hoc e inicie o código carregando o arquivo de modelo de célula; em seguida, faça um pulso bifásico definindo um procedimento como mostrado em Material Suplementar - Criando um pulso bifásico na simulação de neurônios.
         NOTA: Esta etapa cria um pulso bifásico catódico de corrente constante onde os parâmetros de estímulo devem ser declarados pelo usuário ao executar a simulação. Atualmente, a magnitude dos pulsos anódico e catódico é de ±1 μA, mas essa magnitude precisa mudar dependendo da corrente de estimulação fornecida pelo eletrodo de disco.

4. Executando e automatizando várias simulações

1. Combinando os modelos
   1. Extraindo as coordenadas para os nós no modelo de célula de neurônios
      NOTA: O objetivo da combinação das simulações é adquirir os valores de potencial extracelular correspondentes a cada nó do modelo celular. As coordenadas dos dois modelos devem, no entanto, estar alinhadas. Neste exemplo, o segmento central do soma (soma(0,5)) foi alinhado para se deitar no plano médio horizontal do tecido da retina (correspondente à camada de células ganglionares da retina), com o nó central do soma localizado logo acima do centro do eletrodo do disco.
      1. Abra o modelo FEM e observe a coordenada de um ponto de referência (por exemplo, o plano médio horizontal do tecido da retina, acima do centro do eletrodo de disco), caso em que é [0, 0, 131,5] μm.
      2. No conjunto computacional de neurônios, crie um arquivo chamado calculateCoord.hoc para extrair as coordenadas do centroide de cada segmento e deslocar cada seção para que o segmento central do soma tenha a mesma coordenada que o ponto de referência no modelo FEM (Supplementary Material-Calculando a coordenada de cada nó).
   2. Salvando os pontos de coordenadas em um arquivo de texto
      1. Execute o arquivo calculateCoord.hoc (clicando duas vezes no File Explorer ou abrindo a GUI do conjunto computacional de neurônios; em seguida, clique em File > load hoc na barra de ferramentas). Salve as coordenadas para os valores de tensão extracelular a serem avaliados em um arquivo de texto chamado 'coordenadas.dat'.
   3. Executando as simulações e salvando os dados de tensão em um arquivo de texto
      NOTA: Nesta etapa, extraímos os valores extracelulares calculados do modelo FEM, mas só salvaríamos os dados das coordenadas relevantes que coincidem com o centro de cada segmento celular. Siga a etapa 4.1.6.2 quando um grande número de potenciais for necessário para exportar.
      1. Abra o arquivo de modelo de tecido no software FEM; vá para o título Resultados na Árvore Modelo e clique em Exportar Dados > > Dados 1. Verifique se o Conjunto de Dados está definido como Estudo 1/Soluções Paramétricas 1 e digite 'V' na coluna Expressão e 'mV' na coluna Unidade .
      2. Em Saída, altere o Nome do arquivo para extracelular.dat e escolha Pontos a serem avaliados em: Do arquivo. Carregue as coordenadas.dat para o campo Arquivo de coordenadas e clique em Exportar.
   4. Aplicando o pulso bifásico ao modelo de célula
      NOTA: Nesta fase, os valores de tensão extracelular para cada segmento de célula em um ponto de tempo (onde a corrente é de 1 μA) estão disponíveis. Como o estudo pretende submeter a célula a um pulso bifásico, faça com que o valor da voltagem extracelular experimentado pela célula mude com o tempo usando o método 'vector.play'.
      1. Adicione as linhas mostradas no Material Suplementar - Aplicação do pulso bifásico na estimulação.hoc.
   5. Executando a simulação combinada
      NOTA: Um intervalo de tempo 'dt' para as aproximações numéricas precisa ser definido para executar as simulações. Semelhante ao nseg, um dt mais curto pode aumentar a precisão computacional, mas também aumenta o custo computacional.
      1. Adicione as linhas mostradas no Supplementary Material-Executando a simulação de neurônios ao final da estimulação.hoc. Em seguida, clique duas vezes no arquivo stimulation.hoc para carregar o script e executar automaticamente a simulação. O potencial transmembrana do segmento de interesse pode ser exibido na GUI do conjunto computacional de neurônios (etapa 4.2.1) ou salvo em um arquivo de texto para ser lido em outros programas (etapa 4.1.6.1.2). Siga as etapas 4.1.6.1 e 4.1.6.2 se cálculos repetidos e um grande número de potenciais de membrana precisarem ser exportados.
   6. Extra: Automatizando simulações
      NOTA: Para encontrar uma amplitude de limiar, faça um loop da simulação várias vezes com uma amplitude de corrente diferente a cada vez. Outra automação pode ser necessária para encontrar o limiar para neurônios localizados em diferentes posições em relação ao eletrodo estimulante. Uma etapa de automação pode ser feita no conjunto computacional de neurônios usando um procedimento, bem como no software FEM usando um script chamado 'método'.
      1. Automação da simulação de neurônios para encontrar uma amplitude limiar
         NOTA: Um lote de simulações de neurônios pode ser feito automaticamente. As etapas a seguir são implementadas no programa de simulação de neurônios para encontrar as amplitudes limiares dos neurônios sob diferentes parâmetros de estimulação.
         1. Criar um procedimento para repetir a simulação no programa de simulação de neurônios: No stimulation.hoc, crie um vetor para conter uma faixa de amplitude de corrente a ser testada. Em seguida, crie um procedimento para aplicar a amplitude de corrente e registrar qualquer presença de um pico (uma mudança positiva de uma tensão transmembrana negativa para uma positiva), e a amplitude limiar é definida como a menor amplitude de corrente que faz com que um pico ocorra. Para fazer isso, defina um procedimento chamado findTh() (Supplementary Material-Looping over a range of current amplitudes) no final do arquivo stimulation.hoc
         2. Salvando a resposta no limiar para um arquivo de texto: Adicione as seguintes linhas ao procedimento findTh() no stimulation.hoc para armazenar os valores de tensão transmembrana calculados para todos os compartimentos de neurônios de cada etapa de vez em um arquivo de texto:
            sprint(saveFileName, "Response_%d.dat", th) // Armazene o valor limite
            saveFile.wopen(saveFileName)
            para i=0,(responseVector.size()-1){
            saveFile.printf("%g, ", responseVector.x[i])
            if(i==responseVector.size()-1) {saveFile.printf("%g\n", responseVector.x[i])
            saveFile.close(saveFileName)
            }}
      2. Automação no software FEM para encontrar os valores de voltagem para neurônios em diferentes locais
         NOTA: Outra automação que pode ser feita é a aquisição automática de valores de voltagem extracelular para neurônios em diferentes locais. O menu Application Builder no software FEM fornece um meio de definir um 'método' ou um script para automatizar as etapas necessárias para o software executar cálculos. Para demonstrar, a localização da célula na direção x é deslocada 5 vezes em uma etapa de 100 μm (Figura 6 Suplementar).
         1. Escrever um código para automações de simulações de FEM.
            1. Vá para o Application Builder, clique com o botão direito do mouse em Methods na árvore Application Builder, escolha New Method e clique em OK. Vá para Preferências > Métodos de > de Arquivo, marque a caixa Exibir Todos os Códigos e clique em OK.
            2. Escreva um script .hoc que carregará o arquivo de coordenadas, altere os valores para corresponder ao local desejado e salve um arquivo de texto contendo os valores de tensão para o novo local da célula digitando os códigos mostrados no método Supplementary Material-Defining a para automatizar simulações FEM.
         2. Executando as etapas automatizadas no software FEM: Alterne para o Construtor de Modelos, o Desenvolvedor > o Método de Execução > Método 1. Isso produzirá arquivos .dat com os valores de tensão apropriados, chamados extracellular_1.dat, extracellular_2.dat, etc.
      3. Looping das simulações em uma linguagem de programação de uso geral
         NOTA: Para repetir as simulações, o arquivo de texto apropriado precisa ser carregado na simulação do conjunto computacional de neurônios a cada vez, e uma linguagem de programação²⁰ que possa carregar e manipular arquivos de texto facilmente é conveniente para executar esta etapa. Qualquer ambiente de desenvolvimento integrado (IDE) ^{conveniente21} pode ser usado para esta etapa.
         1. Abra o IDE escolhido, clique em Novo arquivo para fazer um novo script. Aqui um arquivo .py é usado neste exemplo. Digite as linhas mostradas em Material Suplementar - Executando as simulações em uma linguagem de programação de uso geral.
         2. Finalmente, clique em Executar ou pressione F5 para executar o script, que também abrirá a GUI (Figura 7 Suplementar).
2. Exibição de dados de simulação
   NOTA: Seguindo todas as etapas acima, os resultados da simulação devem ser armazenados em arquivos de texto, contendo o valor limite e o potencial transmembrana no limiar. No entanto, o usuário tem a opção de exibir o resultado da simulação enquanto a simulação está sendo executada usando a GUI do NEURON.
   1. Represente graficamente a resposta do modelo de neurônios à estimulação extracelular na GUI do conjunto computacional de neurônios. Para fazer isso, execute stimulation.hoc, clique em Graph > Voltage Axis na barra de ferramentas e, na janela do gráfico, clique com o botão direito do mouse em qualquer lugar e escolha Plotar o quê.
   2. Digite 'axon.v(1)' no campo Variável para Gráfico , o que significa que ele irá plotar o potencial transmembrana do último segmento do axônio por passo de tempo.

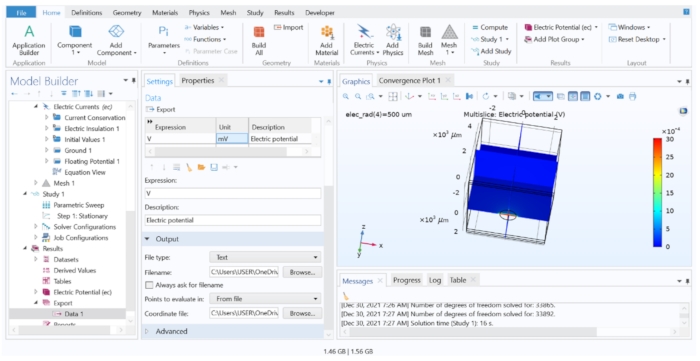
Figura 7: Exibindo e exportando os resultados da computação FEM para um arquivo de texto. A janela Gráficos mostrando um gráfico Multislice do potencial elétrico em V. As opções na Configuração de Exportação de Dados permitiam exportar a variável calculada para um arquivo de texto. Por favor, clique aqui para ver uma versão maior desta figura.

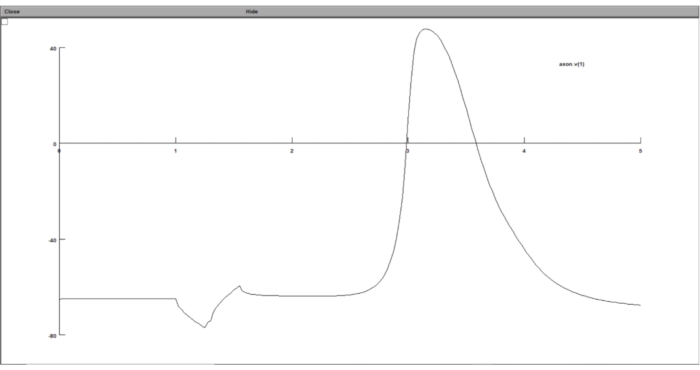
Figura 8: Exibindo o gráfico do potencial transmembranar usando um gráfico de tensão. O potencial transmembrana do neurônio foi exibido na GUI do conjunto computacional de neurônios. O eixo x é o tempo em ms, enquanto o eixo y é o potencial transmembrana do segmento de neurônios escolhido em mV. Por favor, clique aqui para ver uma versão maior desta figura.

Resultados

Foram realizados dois protocolos de simulação para demonstrar o uso do modelo. O primeiro protocolo envolveu a variação do tamanho do eletrodo, mantendo a localização do neurônio e os parâmetros de pulso elétrico iguais. O segundo protocolo envolveu o deslocamento do neurônio na direção x em passos de 100 μm, enquanto o tamanho do eletrodo permaneceu constante. Para ambos os protocolos, o pulso utilizado foi um único pulso bifásico catódico de 0,25 ms de largura com um intervalo interfásico de 0,05 ms. P...

Discussão

Neste artigo, demonstramos um fluxo de trabalho de modelagem que combinou a modelagem de elementos finitos e neurônios biofísicos. O modelo é altamente flexível, pois pode ser modificado em sua complexidade para se adequar a diferentes propósitos, e fornece uma maneira de validar os resultados em relação aos achados empíricos. Também demonstramos como parametrizamos o modelo para permitir a automação.

O método de modelagem em duas etapas combina as vantagens de usar FEM e conjunto ...

Materiais

Name	Company	Catalog Number	Comments
Computer workstation	N/A	N/A	Windows 64-bit operating system, at least 4GB of RAM, at least 3 GB of disk space
Anaconda Python	Anaconda Inc.	Version 3.9	The open source Individual Edition containing Python 3.9 and preinstalled packages to perform data manipulation, as well as Spyder Integrated Development Environment. It could be used to control the simulation, as well as to display and analyse the simulation data.
COMSOL Multiphysics	COMSOL	Version 5.6	The simulation suite to perform finite element modelling. The licence for the AC/DC module should be purchased. The Application Builder capability should be included in the licence to follow the automation tutorial.
NEURON	NEURON	Version 8.0	A freely-distributed software to perform the computation of neuronal cells and/or neural networks.