Source : Yong P. Chen, PhD, département de physique & astronomie, Faculté des sciences, Université de Purdue, West Lafayette, Indiana

Potentiel électrique, également connu sous le nom de « tension », mesure l’énergie potentielle électrique par charge d’unité. Champ électrique est une grandeur scalaire et est fondamental pour de nombreux effets électriques. Comme l’énergie potentielle, ce qui est physiquement significatif est la différence dans le potentiel électrique. Par exemple, la variation spatiale du potentiel électrique est liée au champ électrique, qui donne lieu à la force électrique sur une charge. La différence de potentiel électrique entre deux points dans une résistance entraîne l’écoulement du courant électrique.

Cette expérience utilisera aussi bien un voltmètre et un tube fluorescent pour démontrer le potentiel électrique (plus précisément, la différence de potentiel entre deux points dans l’espace) généré par une sphère chargée. L’expérience démontrera la notion de surfaces équipotentielles, qui sont perpendiculaires aux champs électriques.

Une charge ponctuelle Q située à l’origine (r = 0) produit un potentiel électrique :

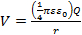(Équation 1)

à n’importe quel point dans l’espace avec une distance r de l’accusation (à l’origine r = 0). Équation 1 décrit également le potentiel électrique produit par une sphère uniformément chargée (centrée à r = 0) avec une charge totale Q dans l’espace en dehors de la sphère (Figure 1). Dans les deux cas, le point de « référence » (où le potentiel est zéro) est à la distance infinie de l’accusation. Le potentiel électrique varie le long de la direction radiale, ce qui est de la direction du champ électrique.

Pour deux points P₁ et P₂ avec distance r₁ et r₂ loin de l’origine (Centre de l’accusation), respectivement, la différence de potentiel entre ces deux points est :

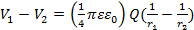(Équation 2)

Si le point P₂ est à l’infini (→∞), ce qui réduit l’équation 2 à l’équation 1. Par conséquent, il y a une différence de potentiel entre deux points si et seulement si ces deux points ont une distance différente de l’origine (Centre de l’accusation). Une surface sphérique centrée à l’origine est une « surface équipotentielle » dans ce cas. Remarque dans ce cas, que le champ électrique (dans le sens radial) est perpendiculaire à la surface équipotentielle (sphère). Cela s’avère être vrai en général : la surface équipotentielle est perpendiculaire à la direction du champ électrique.

Figure 1 : Schéma montrant une sphère chargée reliée à un générateur électrique. Un voltmètre sert à mesurer le potentiel électrique en un point « A » (avec la distance r du centre de la sphère).

1. électrique potentiel en raison d’une sphère chargée

1. Obtenir un générateur van der Graff, qui peut mettre gratuitement sur une sphère métallique. Le centre de la sphère est défini comme l’origine de cette expérience.
2. Obtenir un voltmètre. Connecter (à l’aide de câbles de conducteurs) son « − » terminal à la terre ou la borne sur le générateur de van der Graff de référence ou à un sol (un gros tuyau conducteur) loin (au moins plusieurs mètres) de la génératrice. Connectez la borne « + » à un câble de voltmètre avec une pointe de sonde de tension qui peut être déplacé autour. La connexion schématique est illustrée à la Figure 1.
3. Tournez la manivelle du générateur au moins 10 tours pour charger la sphère.
4. Avec le voltmètre allumé, placer l’extrémité de la sonde de tension (reliée à la borne « + » du voltmètre) environ 0,5 m de l’origine. Utilisez une règle pour mesurer ou marquer la distance au préalable, si vous le souhaitez. Enregistrer la tension mesurée sur le voltmètre. Déplacer la pointe, mais maintenir la distance de l’origine. Observer la lecture du voltmètre.
5. Répétez les étapes ci-dessus avec l’extrémité de la sonde de tension placée à environ 1 m et 1,5 m, respectivement.
6. Obtenir un tube de fluorescence (main). Porter le tube à environ 0,5 m du centre de la sphère chargée ( Figure 2 a). Tout d’abord, orienter le tube pour qu’il soit dans la direction radiale de la sphère. Observer le tube (éteignez les lumières pour faciliter l’observation dans l’obscurité relative). Tournez ensuite le tube de 90 degrés, afin qu’il soit perpendiculaire à la direction radiale ( Figure 2 b). Observer à nouveau le tube.

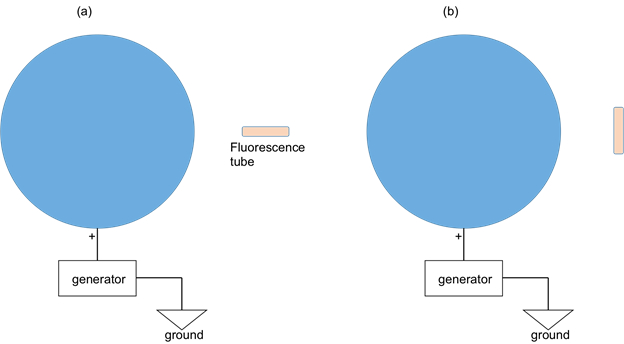
Figure 2: diagramme montrant une sphère chargée reliée à un générateur électrique. Un tube de fluorescence est utilisé pour indiquer la différence de potentiel entre les deux extrémités du tube. Dans le cas de (a) le tube est orienté dans la direction radiale ; et (b) le tube est orientée perpendiculairement à la direction radiale.

Incréments de 1,4 à 1,5, le voltmètre peut être observé à présenter des résultats similaires si l’extrémité de la sonde est maintenue à une distance similaire depuis l’origine (autrement dit, sur une surface équipotentielle). Cependant, la tension chute si la sonde se déplace plus loin loin de l’origine. La tension mesurée à 1 m et 1,5 m de distance sera environ 1/2 et 1/3 de la lecture à 0,5 m, respectivement. Si la tension V mesurée par rapport à la distance inverse (1/r) est tracée, une ligne droite qui entraîne, comme prévu à partir de l’équation 1.

Potentiel électrique (tension) est omniprésent et peut-être les plus couramment utilisés quantité d’électricité. Il est souvent beaucoup plus facile à utiliser le potentiel électrique (qui est un scalaire) que le champ électrique (qui est un vecteur), même si les deux peuvent être liés entre eux. Différence de potentiel électrique est utilisé pour la commande et commande charge motion (accélérer/ralentir/dévier des charges), par exemple dans un écran de télévision ou un microscope électronique. Différence de potentiel électrique (ce que nous appelons habituellement tension) est aussi ce qui anime actuel courant dans un conducteur. Chaque fois qu’on mesure une tension, on mesure la différence de potentiel électrique entre deux points (qui est parfois un point de référence ou au sol définie pour avoir zéro potentiel).

L’auteur de l’expérience reconnaît l’aide de Gary Hudson pour la préparation du matériel et Chuanhsun Li pour démontrer les étapes dans la vidéo.