Fonte: Yong P. Chen, PhD, Departamento de Física & Astronomia, Faculdade de Ciências, Universidade purdue, West Lafayette, IN

O potencial elétrico, também conhecido como "tensão", mede a energia potencial elétrica por carga unitária. O campo elétrico é uma quantidade escalar e é fundamental para muitos efeitos elétricos. Como energia potencial, o que é fisicamente significativo é a diferença no potencial elétrico. Por exemplo, a variação espacial no potencial elétrico está relacionada ao campo elétrico, o que dá origem à força elétrica em uma carga. A diferença no potencial elétrico entre dois pontos em um resistor impulsiona o fluxo de corrente elétrica.

Este experimento usará um medidor de volts e um tubo fluorescente para demonstrar o potencial elétrico (mais precisamente, a diferença potencial entre dois pontos no espaço) gerado por uma esfera carregada. O experimento demonstrará o conceito de superfícies equipotenciais, que são perpendiculares aos campos elétricos.

Uma carga de ponto Q localizada na origem (r = 0) produz um potencial elétrico:

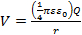(Equação 1)

em qualquer ponto do espaço com uma distância r da carga (na origem r = 0). A equação 1 também descreve o potencial elétrico produzido por uma esfera uniformemente carregada (centrada em r = 0) com carga total Q no espaço fora da esfera(Figura 1). Em ambos os casos, o ponto de referência (onde o potencial é zero) está a uma distância infinita da carga. O potencial elétrico varia ao longo da direção radial, que é a direção do campo elétrico.

Para dois pontos P₁ e P₂ com distância r₁ e r₂ longe da origem (centro da carga), respectivamente, a diferença potencial entre esses dois pontos é:

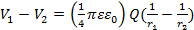(Equação 2)

Se o ponto P₂ estiver no infinito (→∞), isso reduz a Equação 2 à Equação 1. Portanto, há uma diferença potencial entre dois pontos se e somente se esses dois pontos tiverem uma distância diferente da origem (centro da carga). Uma superfície esférica centrada na origem é uma "superfície equipotential" neste caso. Observe que, neste caso, o campo elétrico (ao longo da direção radial) é perpendicular à superfície equipotential (esfera). Isso acaba por ser geralmente verdade: a superfície equipotential é perpendicular à direção do campo elétrico.

Figura 1: Diagrama mostrando uma esfera carregada conectada a um gerador elétrico. Um voltímetro é usado para medir o potencial elétrico em um ponto "A" (com distância r do centro da esfera).

1. Potencial elétrico devido a uma esfera carregada

1. Obtenha um gerador van der Graff, que pode colocar carga em uma esfera metálica. O centro da esfera é definido como a origem deste experimento.
2. Obtenha um voltímetro. Conecte (usando cabos condutores) seu terminal "−" ao solo ou terminal de referência no gerador van der Graff, ou a um solo elétrico (como um grande tubo de condução) distante (pelo menos vários metros) do gerador. Conecte seu terminal "+" a um cabo voltmeter com uma ponta de sonda de tensão que pode ser movida ao redor. A conexão esquemática é mostrada na Figura 1.
3. Gire a manivela do gerador em pelo menos 10 voltas para carregar a esfera.
4. Com o voltímetro ligado, coloque a ponta da sonda de tensão (conectada ao terminal "+" do voltímetro) a cerca de 0,5 m de distância da origem. Use uma régua para medir ou marcar a distância de antemão, se desejar. Regisso dia a leitura da tensão no voltímetro. Mova a ponta ao redor, mas mantenha a distância longe da origem. Observe a leitura do voltímetro.
5. Repita o passo acima com a ponta da sonda de tensão colocada em cerca de 1 m e 1,5 m, respectivamente.
6. Obtenha um tubo de fluorescência (portátil). Leve o tubo a cerca de 0,5 m de distância do centro da esfera carregada (Figura 2a). Primeiro, oriente o tubo para que ele esteja ao longo da direção radial longe da esfera. Observe o tubo (desligue as luzes para facilitar a observação em relativa escuridão). Em seguida, gire o tubo em 90 graus para que seja perpendicular à direção radial (Figura 2b). Observe o tubo novamente.

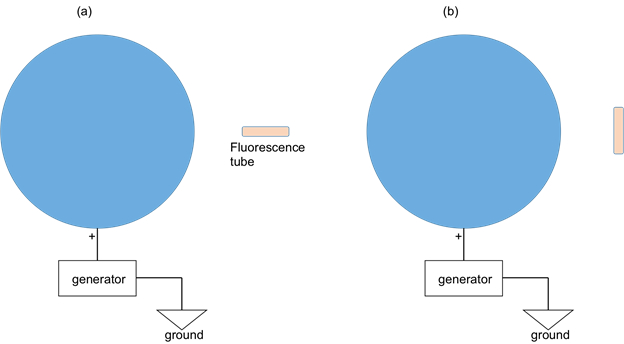
Figura 2: Diagrama mostrando uma esfera carregada conectada a um gerador elétrico. Um tubo de fluorescência é usado para indicar a diferença potencial entre as duas extremidades do tubo. No caso de ( a) o tubo é orientado ao longo da direção radial; e ( b) o tubo é orientado perpendicular à direção radial.

Nas etapas 1.4-1.5, o voltímetro pode ser observado para dar leituras semelhantes se a ponta da sonda for mantida a distâncias semelhantes da origem (isto é, em uma superfície equipotential). No entanto, a tensão cai se a sonda se afastar mais da origem. A leitura de tensão a 1 m e 1,5 m de distância será de cerca de 1/2 e 1/3 da leitura a 0,5 m de distância, respectivamente. Se a tensão V medida versus a distância inversa (1/r) for traçada, uma linha reta resulta, como esperado da Equação 1.

O potencial elétrico (tensão) é onipresente e talvez a quantidade mais utilizada em eletricidade. Muitas vezes é muito mais conveniente usar potencial elétrico (que é um escalar) do que campo elétrico (que é um vetor), mesmo que os dois possam estar relacionados um com o outro. A diferença potencial elétrica é usada para dirigir e controlar o movimento de carga (acelerar/desacelerar/desviar cargas), por exemplo, em uma tela de TV ou microscópio eletrônico. Diferença potencial elétrica (o que costumamos chamar de tensão) é também o que impulsiona o fluxo de corrente em um condutor. Sempre que se mede uma tensão, a gente mede a diferença de potencial elétrico entre dois pontos (um dos quais às vezes é um ponto de referência ou um solo definido para ter zero potencial).

O autor do experimento reconhece a ajuda de Gary Hudson para a preparação do material e Chuanhsun Li por demonstrar os passos no vídeo.