14.15 : Kepler's First Law of Planetary Motion

In the early 17th century, German astronomer and mathematician Johannes Kepler postulated three laws for the motion of planets in the solar system. He formulated his first two laws based on the observations of his forebears, Nikolaus Copernicus and Tycho Brahe.

Polish astronomer Nikolaus Copernicus put forth a theory that stated a heliocentric model for the solar system. According to this heliocentric theory, all the planets, including Earth, orbit the Sun in circular orbits.

On the other hand, Danish astronomer Tycho Brahe, the employer of Johannes Kepler, had meticulously recorded the position of every planet in detail. For most visible planets, these observations were in accordance with the Copernican heliocentric theory, except for the planet Mars.

While analyzing the Mars data of Tycho Brahe, Johannes Kepler realized that the Copernican theory was accurate except that planets revolve around the Sun in an elliptical orbit rather than circular orbits. This led him to his first law of planetary motion, which states that every planet travels along an ellipse, with the Sun located at one of the ellipse's foci.

An ellipse is an elongated circle. The degree of elongation of an ellipse is expressed using a parameter called eccentricity.

An axis of an ellipse along the elongation is called the major axis a, and the one perpendicular to it is the minor axis b. Therefore, the eccentricity of an ellipse is expressed as

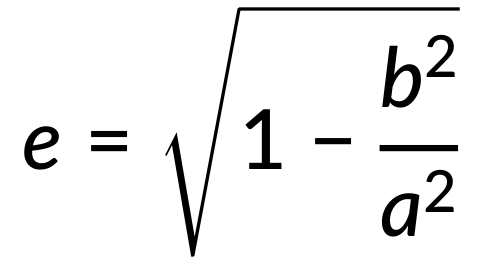
Since b < a, the eccentricity of an ellipse is always less than unity. For a circle, a = b, hence the eccentricity of a circle is zero.

The eccentricity of Martian orbit is 0.0935. It is considered to have the most eccentric orbit after Mercury, whose eccentricity is 0.21. Earth's orbit has an eccentricity of 0.0167.

Since planets are in elliptical orbits with the Sun at one of the foci, their radial distances change throughout the year. Their closest distance from the Sun is known as the perigee, while the farther distance is called the apogee.

This text is adapted from Openstax, University Physics Volume 1, Section 13.5 Kepler's Laws of Motion.