14.15 : Kepler's First Law of Planetary Motion
In the early 17th century, German astronomer and mathematician Johannes Kepler postulated three laws for the motion of planets in the solar system. He formulated his first two laws based on the observations of his forebears, Nikolaus Copernicus and Tycho Brahe.
Polish astronomer Nikolaus Copernicus put forth a theory that stated a heliocentric model for the solar system. According to this heliocentric theory, all the planets, including Earth, orbit the Sun in circular orbits.
On the other hand, Danish astronomer Tycho Brahe, the employer of Johannes Kepler, had meticulously recorded the position of every planet in detail. For most visible planets, these observations were in accordance with the Copernican heliocentric theory, except for the planet Mars.
While analyzing the Mars data of Tycho Brahe, Johannes Kepler realized that the Copernican theory was accurate except that planets revolve around the Sun in an elliptical orbit rather than circular orbits. This led him to his first law of planetary motion, which states that every planet travels along an ellipse, with the Sun located at one of the ellipse's foci.
An ellipse is an elongated circle. The degree of elongation of an ellipse is expressed using a parameter called eccentricity.

An axis of an ellipse along the elongation is called the major axis a, and the one perpendicular to it is the minor axis b. Therefore, the eccentricity of an ellipse is expressed as
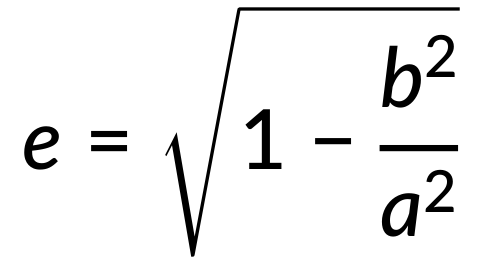
Since b < a, the eccentricity of an ellipse is always less than unity. For a circle, a = b, hence the eccentricity of a circle is zero.
The eccentricity of Martian orbit is 0.0935. It is considered to have the most eccentric orbit after Mercury, whose eccentricity is 0.21. Earth's orbit has an eccentricity of 0.0167.
Since planets are in elliptical orbits with the Sun at one of the foci, their radial distances change throughout the year. Their closest distance from the Sun is known as the perigee, while the farther distance is called the apogee.
This text is adapted from Openstax, University Physics Volume 1, Section 13.5 Kepler's Laws of Motion.
章から 14:

Now Playing
14.15 : Kepler's First Law of Planetary Motion
重力
3.8K 閲覧数

14.1 : 引力
重力
6.0K 閲覧数

14.2 : ニュートンの重力の法則
重力
11.8K 閲覧数

14.3 : 球対称質量間の引力
重力
814 閲覧数

14.4 : 球体間の重力
重力
8.1K 閲覧数

14.5 : 質量座標の縮小: 孤立した 2 体問題
重力
1.2K 閲覧数

14.6 : 地球上の重力による加速度
重力
10.4K 閲覧数

14.7 : 他の惑星の重力による加速
重力
4.0K 閲覧数

14.8 : 見かけの重量と地球の自転
重力
3.5K 閲覧数

14.9 : 地表付近の重力による加速度の変動
重力
2.3K 閲覧数

14.10 : 重力による位置エネルギー
重力
5.1K 閲覧数

14.11 : 重ね合わせの原理と重力場
重力
1.2K 閲覧数

14.12 : 脱出速度
重力
5.1K 閲覧数

14.13 : 衛星の円軌道と臨界速度
重力
2.8K 閲覧数

14.14 : 円軌道上の衛星のエネルギー
重力
2.1K 閲覧数
See More
Copyright © 2023 MyJoVE Corporation. All rights reserved