13.13 : Kendall's Tau Test

Kendall's tau test, also known as the Kendall rank coefficient test, is a nonparametric method for assessing association between two variables. This test is particularly useful for identifying significant correlations when the distributions of the sample and population are unknown. Developed in 1938 by the British statistician Sir Maurice George Kendall, the tau coefficient (denoted as τ) serves as a rank correlation coefficient, with values ranging from -1 to +1.

A τ value of +1 indicates that the ranks of the two variables are perfectly similar, suggesting a strong positive correlation. Conversely, a τ value of -1 indicates that the ranks are perfectly dissimilar, suggesting a strong negative correlation. A positive τ value indicates a positive relationship between the variables, while a negative τ value signifies a negative relationship. This test is a valuable tool for analyzing ordinal data and exploring relationships without relying on strict assumptions about the underlying distributions.

Kendall's τ is a relatively straightforward calculation when there are no ties in the data ranks. The coefficient equation is:

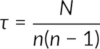
In Kendall's tau test, calculating the quantity N from the ranks is crucial for determining the strength of the correlation between two variables. There are conventional methods as well as alternative approaches for this calculation. One common method involves arranging the data into two columns: the first column contains the rankings of the first variable (e.g., artisan rankings), while the second column lists the corresponding ranks of the second variable.

To visualize the relationships, lines are drawn to connect the same ranks between the two columns—connecting rank 1 in the first column with rank 1 in the second, rank 2 with rank 2, and so on. After establishing these connections, the total number of intersections formed by these lines is counted, denoted as X. This count is then used to calculate N using the following equation:

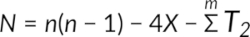
Kendall's tau test is similar to Spearman's rank test. Both of these tests are equivalent and precise, and there is no rule of thumb or conditions in which either of the tests could be more beneficial. Kendall's tau calculation is, however, more straightforward when there are no ties in the data ranks and is more widely used for such data in general.