18.1 : Conservation of Mass in Finite Cotrol Volume

The principle of conservation of mass is a fundamental law in fluid mechanics and is applied using the continuity equation. We apply the concept to a finite control volume to derive the continuity equation.

A system is defined as a collection of unchanging contents, and the conservation of mass states that a system's mass is constant.

Where M_sys is the mass of the system. The mass of the system can be written as:

Consider a fixed, non-deforming control volume that coincides with the system at a particular instant.

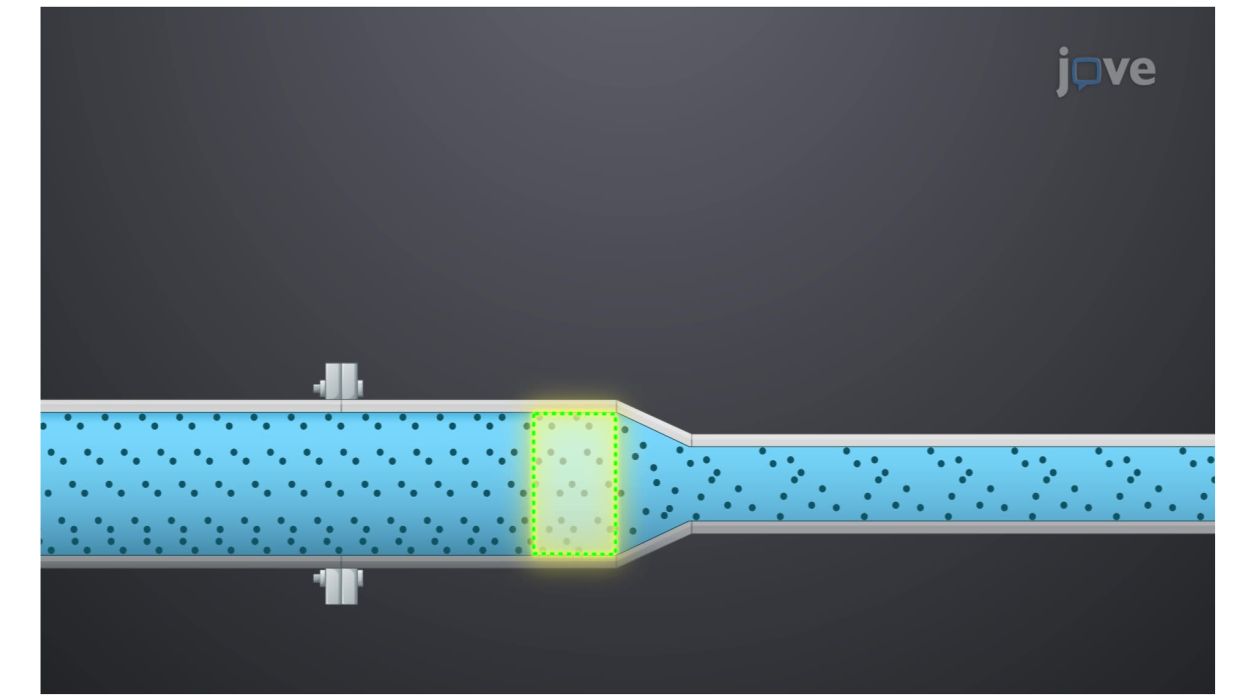
Using the Reynolds transport theorem, we express the time rate of change of the system mass:

This equation breaks the change in mass into two parts:

1. Accumulation of mass inside the control volume.
2. Net mass flow through the control surface surrounding the control volume.

For steady-state flow, where the fluid properties (like density) remain constant over time, the time derivative term vanishes:

This states that the net mass flow through the control surface must be zero; what flows into the control volume must flow out. The continuity equation retains both terms for unsteady flows or flows where properties like density change over time. This form is used for more complex situations, such as transient flow in pipelines or fluctuating flow in rivers due to dam releases.

In real-world applications, such as the design of pipe systems, engineers use the continuity equation to maintain a consistent flow rate. When a pipe's diameter changes, the fluid's velocity adjusts accordingly to ensure the same mass flow rate is preserved. This principle is crucial for designing systems that manage variable flow rates, such as drainage systems.