Fonte: Ketron Mitchell-Wynne, PhD, Asantha Cooray, PhD, Dipartimento di Fisica e Astronomia, Scuola di Scienze Fisiche, Università della California, Irvine, CA

L'energia potenziale è un concetto importante in fisica. L'energia potenziale è l'energia associata alle forze che dipendono dalla posizione di un oggetto rispetto all'ambiente circostante. L'energia potenziale gravitazionale, che viene discussa in un altro video, è l'energia associata che è direttamente proporzionale all'altezza di un oggetto dal suolo. Allo stesso modo, è possibile definire l'energia potenziale della molla, che è direttamente proporzionale allo spostamento di una molla dal suo stato rilassato. Una molla allungata o compressa ha energia potenziale, in quanto ha la capacità di lavorare su un oggetto. La "capacità di fare lavoro" è spesso citata come la definizione fondamentale di energia.

Questo video dimostrerà l'energia potenziale immagazzinata nelle molle. Verificherà anche l'equazione della forza di ripristino delle molle, o la legge di Hooke. La costante della molla è diversa per le molle di diverse elasticità. Verrà verificata la legge di Hooke e misurata la costante della molla attaccando pesi variabili a una molla sospesa e misurando gli spostamenti risultanti.

1. Misurare la costante della molla e l'energia potenziale di una molla e confermare la relazione tra la massa e il periodo oscillatorio T.

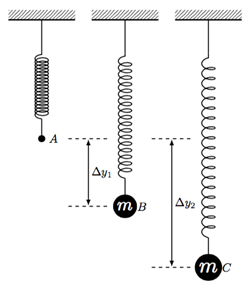
1. Ottenere una molla con una costante di molla nota, un supporto a cui fissare la molla, almeno 5 pesi di varie masse che possono essere attaccati alla molla, un bastone metro e un cronometro.
2. Fissare il supporto a una solida base e fissare la molla al supporto. Assicurati che ci sia abbastanza spazio sotto la molla perché si allunghi senza colpire il tavolo o il te

I risultati rappresentativi dell'esperimento, condotto con una molla di costante k = 10 N/m, sono mostrati nella Tabella 1. Il grafico di F rispetto allo spostamento Δy è tracciato di seguito nella Figura 2. La funzione lineare è adatta a una linea e la pendenza della linea è uguale alla costante della molla, entro un margine di errore. La linearità del risultato mostra la validità della legge di Hooke (Equazione 1).

L'uso delle molle è onnipresente nella nostra vita quotidiana. La sospensione delle auto moderne è realizzata con molle adeguatamente smorzate. Ciò richiede la conoscenza delle costanti di primavera. Per le corse Cadillac più fluide, vengono utilizzate molle con una costante di molla inferiore e la corsa è "mushier". Le auto ad alte prestazioni utilizzano molle con una costante di molla più elevata per una migliore maneggevolezza. I trampolini sono anche realizzati con molle di diverse costanti primaverili, a secon...