5.8 : 분자 속도와 운동에너지

운동 분자 이론은 다양한 가스 법칙에 의해 기술된 행동을 질적으로 설명합니다. 이 이론의 추정은 이러한 개별 법률을 파생하기 위해 보다 정량적 인 방식으로 적용 될 수있다.

총체적으로, 가스의 견본에 있는 분자는 평균 운동 에너지 및 평균 속도; 그러나 개별적으로, 그들은 다른 속도로 이동합니다. 분자는 종종 운동량이 보존되는 탄성 충돌을 겪습니다. 충돌 하는 분자는 다른 속도로 편향 되기 때문에, 개별 분자는 광범위 하 게 다양 한 속도. 그러나, 관련된 분자와 충돌의 광대 한 수 때문에, 분자 속도 분포 및 평균 속도는 일정. 이 분자 속도 분포는 맥스웰-볼트만 분포로 알려져 있으며, 주어진 속도를 가진 가스의 대량 샘플에서 분자의 상대적 수를 묘사합니다.

질량(m)및속도(u)의입자의 운동 에너지(KE)는 다음과 같은 양으로 주어집니다.

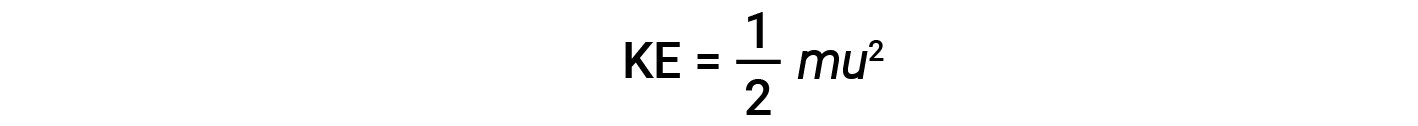
킬로그램단위로 질량을 발현하고 초당 미터 단위로 속도를 내면 줄 단위로 에너지 값이 생성됩니다(J = kg·m^2/s2). 많은 수의 가스 분자를 처리하기 위해, 우리는 속도와 운동 에너지 모두에 평균을 사용합니다. KMT에서, 입자의 루트 평균 제곱 속도, u_rms는 n = 입자 수를 가진 속도의 제곱의 정사각형 루트로 정의됩니다.

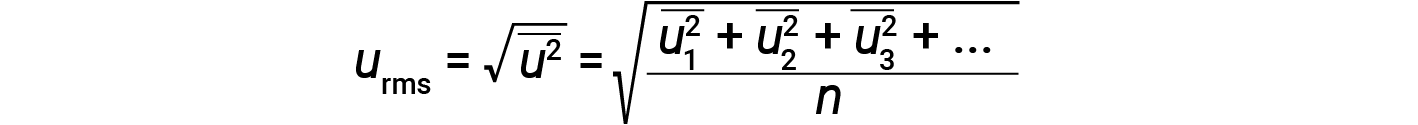
입자의 두더지, KE_평균의평균 운동 에너지는 다음과 같습니다 .

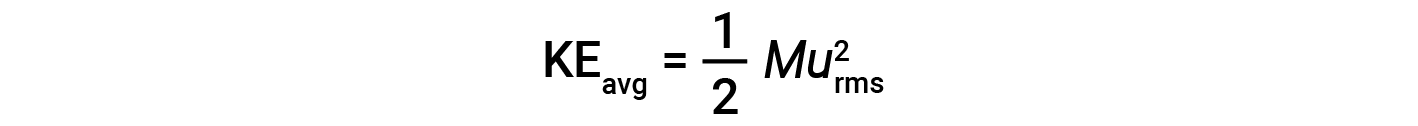
여기서 M은 kg/mol 단위로 발현되는 어금니 질량입니다. 가스 분자의 두더지의 KE_평균은 또한 가스의 온도에 직접 비례하고 방정식에 의해 설명 될 수있다 :

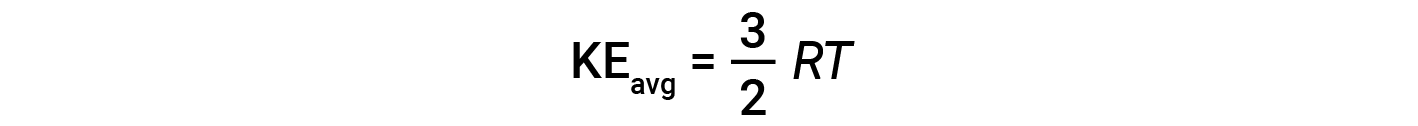
여기서 R은 가스 상수이고 T는 켈빈 온도입니다. 이 방정식에 사용되는 경우, 가스 상수의 적절한 형태는 8.314 J/mol⋅K(8.314 kg·m^2/s2·mol·mol·당대· K). KE_평균에 대한 이 두 개의 개별 방정식은 분자 속도와 온도 사이의 관계를 산출하기 위해 결합및 재배열 될 수 있습니다:

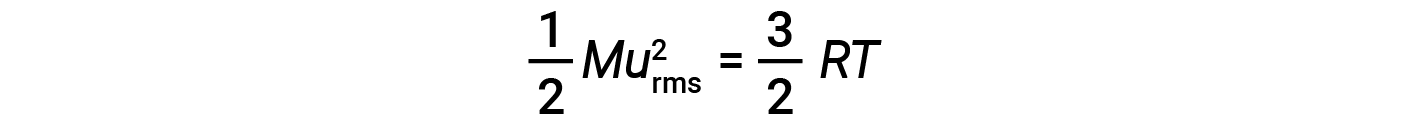
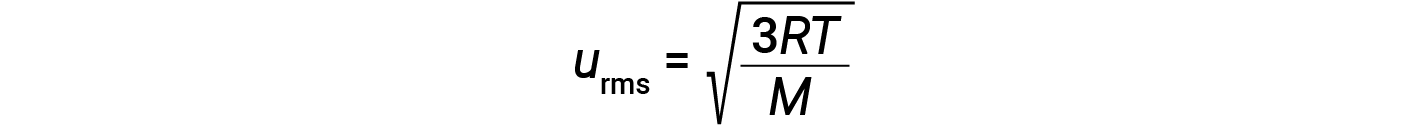
가스의 온도가 증가하면 KE_평균이 증가하고, 더 많은 분자가 더 빠른 속도를 가지며, 분포는 전체적으로 더 높은 속도, 즉 오른쪽으로 이동합니다. 온도가 감소하면 KE_AVG가 감소하고, 더 많은 분자가 더 낮은 속도를 가지며, 분포는 전체적으로 더 낮은 속도, 즉 왼쪽으로 이동합니다.

주어진 온도에서 모든 가스는 분자에 대해 동일한 KE_평균을 갖습니다. 가스의 분자 속도는 분자 질량과 직접 관련이 있습니다. 가벼운 분자로 구성된 가스는 고속 입자가 더 많고 u_rms가높으며, 속도 분포는 상대적으로 높은 속도로 정점에 도달합니다. 더 무거운 분자로 구성된 가스는 더 낮은 속도 입자, 낮은 u_rms및 상대적으로 낮은 속도로 피크 속도 분포를 갖는다.

이 텍스트는 Openstax, 화학 2e, 섹션 9.5: 운동 분자 이론에서 적용됩니다.