분산 된 피크 위치와 결정 구조 사이의 관계 :

충분히 작은 파장의 광파가 결정 격자에 발생하면 격자 점에서 확산됩니다. 특정 각도의 발생각도에서, 확산된 병렬 파는 건설적으로 간섭하고 강도에서 검출 가능한 피크를 생성합니다. W.H. Bragg는 그림 1에 설명된 관계를 식별하고 해당 방정식을 파생했습니다.

nλ = 2d_hkl 죄 θ [1]

여기서 λ는 사용되는 X선의 파장이며, d_hkl은 (hkl) 밀러 지수*를 가진 특정 평면 세트 사이의 간격이며, θ는 회절 피크를 측정하는 발생각이다. 마지막으로 n은 회절의 '고조파 질서'를 나타내는 정수입니다. 예를 들어, n=1에서, 우리는 첫 번째 고조파를 가지며, 이는 결정(2d_hkl sin에 해당)을 통해 확산되는 X선의 경로가 정확히1λ이며,n=2에서, diffracted 경로는2λ임을의미한다. 일반적으로 n=1을 가정할 수 있으며, 일반적으로 θ <^죄에대한 n=1(2λ/d_h'k'l'), h'k'l'은 회절 실험에서 첫 번째 피크(가장 낮은 2θ 값)를 표시하는 평면의 밀러 지수입니다. 밀러 지수는 결정 내의 방향과 평면을 식별하기위한 표기법 시스템을 구성하는 세 정수의 집합입니다. 방향의 경우 [h k l] 밀러 지수는 방향을 따라 두 점의 각각 x, y 및 z 좌표(카르테시안 좌표 시스템에서)의 정규화된 차이를 나타냅니다. 비행기의 경우 비행기의 밀러 지수(h k l)는 단순히 비행기에 수직인 방향의 h k l 값입니다.

반사 모드에서 일반적인 XRD 실험에서 X선 소스는 위치에 고정되고 샘플은 θ 위에 X선 빔에 대하여 회전됩니다. 검출기는 분산 빔을 집어 들고 두 배의 속도로 회전하여 샘플 회전을 따라가야 합니다(즉, 주어진 샘플 각도의 경우, 검출기 각도는 2θ). 실험의 형상은 그림 1에 괄호로 표시됩니다.

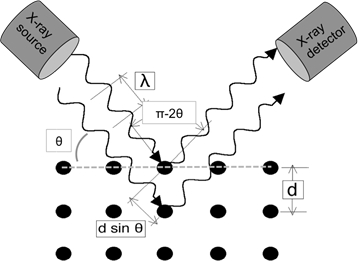
그림 1: 브래그 법칙 그림.

강도의 피크가 관찰되면 방정식 1이 반드시 만족됩니다. 따라서 이러한 피크가 관찰되는 각도에 따라 d 간격을 계산할 수 있습니다. 여러 봉우리의 d-간격을 계산함으로써, 결정 클래스 및 결정 구조 파라미터 재료 샘플은 사용되는 XRD 소프트웨어와 함께 제공되는 하나왈트 검색 매뉴얼 또는 데이터베이스 라이브러리와 같은 데이터베이스를 사용하여 식별될 수 있다.

조사 중인 시료가 단일 결정이 아니라고 가정합니다. 샘플이 샘플 표면과 평행한 특정(h*k*l*) 평면이 있는 단일 결정인 경우, 잠재적으로 더 높은 고조파(h*k*l*) 피크(예를 들어, 2)에서 더 높은 각도로 확산 강도(n=1)의 피크를 보려면 브래그 조건이 만족할 때까지 회전해야 합니다. 다른 모든 각도에서 단일 결정 샘플에는 피크가 없을 것입니다. 대신, 시료가 다결정성이거나 분말이라고 가정해 봅시다. 이 가정하에 샘플은 임의로 지향되는 곡물로 구성되며 가능한 모든 격자 평면이 확산될 확률이 유사합니다.

d_hkl과 단위 세포 매개변수 사이의 관계는 7 개의 결정 클래스, 입방, 테트라고날, 육각형, 골수, orthorhombic, 모노 클리닉 및 트리 클리닉에 대한 방정식 2-7에서 아래와 같습니다. 단위 셀 매개 변수는 7 결정 클래스에 대한 단위 셀의길이(a,b, γ)와 (α, β, γ) 사이의 각도로 구성됩니다(그림 1x는 결정 클래스 중 하나의 예를 보여줍니다: a=b≠c, 및 α=β=γ=90^0). 여러 분산 피크 위치(예: 여러 고유 d_hkl 값)를 사용하여 단위 셀 매개변수의 값을 고유하게 해결할 수 있습니다.

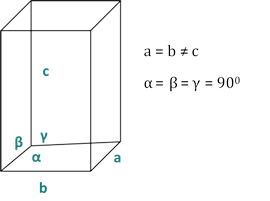
그림 2: 일곱 가지 결정 클래스 중 하나로서 테트라고날 구조.

입방 (a = b = c; α = β = γ = 90^0):

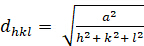[2]

테트라고날 (a = b ≠ c; α = β = γ = 90^0):

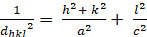[3]

육각형 (a = b ≠ c; α = β = 90⁰; γ = 120^0):

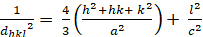[4]

Orthorhombic (≠ b ≠ c; α = β = γ = 90^0):

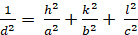[5]

심부 헤랄 (a = b ≠ c; α = β = γ = 90^0):

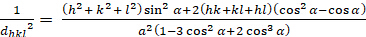[6]

모노 클리닉 (≠ b ≠ c; α = γ = 90⁰ ≠ β):

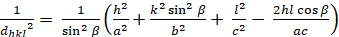[7]

트라이 클리닉 (≠ b ≠ c; α ≠ β ≠ γ ≠ 90^0):

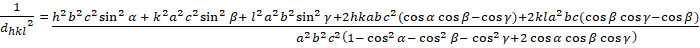      [8]

디프액드 피크 강도와 결정 구조 간의 관계:

다음으로 XRD 패턴의 강도에 기여하는 요인을 살펴봅시다. 계수는 1) 재료의 고유한 구조적 측면(구조내의 산란 원자의 특정 유형 및 위치)과 2) 재료에 특이적이지 않은 분란에 대한 기여도가 1로 분해될 수 있다. 전자에서는 '흡수 계수'와 '구조 계수'의 두 가지 요인이 있습니다. 흡수 계수는 주로 안팎으로 엑스레이를 흡수하는 재료의 능력에 달려 있습니다. 이 계수는 샘플이 얇지 않은 한 θ 의존성을 갖지 않습니다(샘플은 X선의 감쇠 길이보다 3배 더 >). 즉, 다른 피크의 강도에 대한 흡수 계자에 의한 기여도는 일정하다. '구조 계수'는 구조의 직접적인 결과로 특정 피크의 강도에 직접적인 영향을 미칩니다. 나머지 요인은 같은 패밀리에 속한 모든 평면을 대칭적으로 관련시키기 때문에 차지하는 '복합성'과 XRD 실험의 기하학에서 나오는 'Lorentz-편광' 계수는 피크의 상대적 강도에도 영향을 미치지만 재료에 만연하지 않고 분석(i.e.xRD)을 사용하여 쉽게 설명할 수 있습니다.

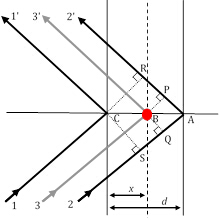
그림 3: 3개의 회절 광선 경로, 그 중 광선 11' 및 22'는 브래그 상태를 만족시키고, 레이 33'은 임의의 위치에서 원자(빨간색 원)에 의해 산란됩니다.

XRD 피크의 상대적 강도에 대한 재료의 고유한 구조적 기여를 전달하는 유일한 요소로서 구조 계수는 매우 중요하며 자세히 살펴볼 필요가 있습니다. 그림 2에서, 우리는 1^st 순서 브래그 회절 조건 (기억, 이것은 n =1에 해당) h00 방향으로 두 원자 평면에 흩어져있는 광선_11'과 레이₂₂ 사이에 만족한다고 가정하자 (밀러 지수 표기표 를 사용하여) 거리 D에 의해 분리. 이 조건하에서, 선_11과 선_{22 사이의} 경로 길이의 차이는 δ_(22'-11') = SA + AR = λ입니다. 따라서, diffracted 광선 1과 2 사이의 위상 이동은, 따라서, Φ_22'-11' = (δ_(22'-11')/λ) 2π =2π (입방 대칭을 가정하 되 고, 따라서, d = h00 방향으로/h]이다.

분석 기하학에서 몇 단계와 함께, 위상 시프트, Φ_(33'-11'),임의의 거리 x간격화 된 원자의 임의평면에 의해 선 3 확산을 표시 할 수 있습니다 x, 에 의해 주어진다: Φ_(33'-11') = 2πhu,여기서 u =x/a (a) u=x/a(h)의 세포 파라미터(a) 방향(a)의 세포 파라미터(a) 방향 다른 직교 방향(0k0) 및 (00l) 및 v=y/a 및 w=z/a를 y-및 z 방향의 분수 좌표로 복용하면 위상 이동식은 Φ =2π(hu+kv+lw)로 확장된다. 지금, 단위 셀에서 j-th원자에 의해 산란된 X선 파는 f_j의 산란 진폭과 Φ_j의위상을 가지게 되며, 이를 설명하는 기능이 있는 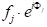것이다. 따라서 우리가 추구하는 구조 요소는 단위 셀의 모든 고유 원자로 인해 모든 산란 함수의 합입니다. 이 구조 계수 인자 F는 다음과 같이 제공됩니다.

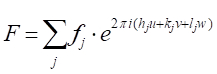[9]

구조계에 의해 기진되는 강도계는 I = F^2이다.

특정 평면(h,k,l)의 원자의 위치(u,v,w)에 기초하여, 건설적이거나 파괴적이거나 그 사이에 흩어진 파도 사이에 간섭이 발생할 가능성이 있으며, 이러한 간섭은 (hkl) 평면을 나타내는 XRD 봉우리의 진폭에 직접적인 영향을 미친다.

지금, 강도의 플롯, I, 대 2θ는 XRD 실험에서 측정되는 것입니다. 결정형 및 관련 단위 세포파라미터(a, b, c, α, β 및 γ)의결정은 방정식 2-9를 사용하여, 데이터베이스와 값을 비교하고, 공제 및 제거 과정을 사용하여 피크의 체계적인 존재/부재를 관찰함으로써 진상적으로 도달될 수 있다. 요즘, 이것은 공정은 결정 구조 데이터베이스에 연결된 다양한 소프트웨어에 의해 상당히 자동화됩니다.

그림 4에서 우리는 Ni 분말 샘플에 대한 XRD 피크를 볼 수 있습니다. 관찰되는 봉우리(예: {111}, {200})는 h, k및 l의모든 모든 홀수 조합이 있는 봉우리들을 위한 것입니다. Ni는 얼굴 중심의 입방체(FCC)이며, 모든 FCC 구조에서 h, k및 l이 균일하고 이상한 정수의 혼합물인{hkl}평면에 대응하는 피크는 산란된 X선의 파괴적인 간섭으로 인해 결석한다. {210} 및 {211} 같은 평면에 해당하는 피크가 없습니다. 이 현상은 체계적인 존재 및 부재 규칙이라고 하며 시료의 결정 구조를 평가하기 위한 분석 도구를 제공합니다.

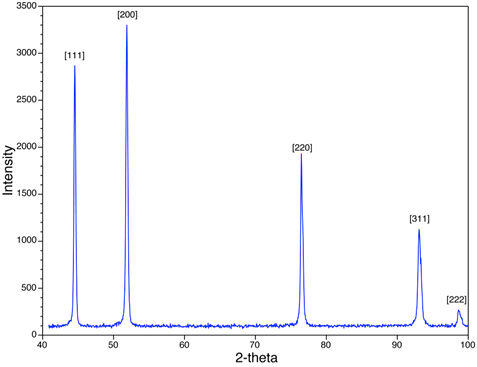
그림 4: 얼굴 중심의 입방 구조를 가진 Ni의 XRD 스캔이 표시됩니다.

이것은 표준 XRD 실험의 데모입니다. 이 실험에서 검사된 물질은 분말 형태로 진행되었지만, 샘플이 샘플 스테이지의 평면과 평행하게 설정할 수 있는 평평한 표면을 가지고 있는 한 XRD는 고체 재료와 동등하게 잘 작동한다.

XRD는 재료에서 결정적 순서의 존재(또는 부재)를 결정하는 상당히 유비쿼터스 방법입니다. 결정 구조를 결정하는 표준 적용 을 넘어, XRD는 종종 다음과 같은 다른 구조적 정보의 다양한 얻기 위해 사용된다 :

1. 재료의 구조가 비정질인지 여부 (회절 강도의 넓은 고비를 특징으로하고 식별 할 수있는 결정성 피크의 부족),
2. 시료가 다중 결정상으로 구성된 복합 재료인지, 그렇다면 각 단계의 분획을 결정합니다.
3. 재료가 비정질/결정성 복합체인지 여부 결정
4. 재료의 입자/입자 크기를 결정하고,
5. 재료의 질감 정도(곡물의 바람직한 방향)를 결정합니다.