Topographical Estimation of Visual Population Receptive Fields by fMRI

Podsumowanie

It is important to obtain unbiased estimates of visual population receptive fields (pRFs) by functional magnetic resonance imaging. We use mild regularization constraints to estimate pRF topography without a-priori assumptions about pRF shape, allowing us to choose specific pRF models post-hoc. This is particularly advantageous in subjects with visual-pathway lesions.

Streszczenie

Visual cortex is retinotopically organized so that neighboring populations of cells map to neighboring parts of the visual field. Functional magnetic resonance imaging allows us to estimate voxel-based population receptive fields (pRF), i.e., the part of the visual field that activates the cells within each voxel. Prior, direct, pRF estimation methods¹ suffer from certain limitations: 1) the pRF model is chosen a-priori and may not fully capture the actual pRF shape, and 2) pRF centers are prone to mislocalization near the border of the stimulus space. Here a new topographical pRF estimation method² is proposed that largely circumvents these limitations. A linear model is used to predict the Blood Oxygen Level-Dependent (BOLD) signal by convolving the linear response of the pRF to the visual stimulus with the canonical hemodynamic response function. PRF topography is represented as a weight vector whose components represent the strength of the aggregate response of voxel neurons to stimuli presented at different visual field locations. The resulting linear equations can be solved for the pRF weight vector using ridge regression³, yielding the pRF topography. A pRF model that is matched to the estimated topography can then be chosen post-hoc, thereby improving the estimates of pRF parameters such as pRF-center location, pRF orientation, size, etc. Having the pRF topography available also allows the visual verification of pRF parameter estimates allowing the extraction of various pRF properties without having to make a-priori assumptions about the pRF structure. This approach promises to be particularly useful for investigating the pRF organization of patients with disorders of the visual system.

Wprowadzenie

Functional magnetic resonance imaging (fMRI) measures non-invasively the functional organization of visual cortex at a macroscopic scale (typically on the order of millimeters). Early fMRI retinotopy studies used a coherence measure between stimulus location and elicited BOLD responses^4-7. These studies typically did not estimate population receptive field size. Later, Dumoulin and Wandell¹ proposed a method to overcome such a limitation by explicitly modeling the pRF location and size, using a linear function of this model to predict the BOLD response. However, one limitation of this pioneering method is that the parametric pRF model has to be chosen a-priori, and may lead to erroneous pRF estimates if it turns out not to be appropriate.

To overcome limitations of the parametric pRF-model method, new methods have been developed recently. These methods directly predict the BOLD response to the stimulus by reconstructing the pRF topography. A method⁸ proposed by Greene and colleagues reconstructs the pRF topography by back-projecting the BOLD responses to the individual 1D stimulus spaces and building the pRF topography in the 2D stimulus space like a typical computer tomography technique. On the other hand, the method² proposed by us directly estimates the 2D pRF topography by using linear regression and applying a regularization technique. In this method, the pRF topography is represented as a set of weights which is multiplied by the stimulus to estimate the neuronal population response of a given voxel. Then, the final Blood Oxygen Level-Dependent (BOLD) response evoked by the stimulus is estimated by convolving the neuronal population response and the canonical hemodynamic response function. In order to solve the under-constrained linear system, additionally, ridge regression regularization is used to enforce sparseness (see Figure 1 below). The regularization technique suppresses noise and artifacts and thus allows our method to estimate the pRF topography more robustly.

The topographical methods do not force the pRF shape to have a certain parametric shape, and therefore can uncover the actual pRF structure. An appropriate parametric model can then be chosen based on the pRF topography. For example, the pRF topography can be used to separate the pRF center and surround, and then the subsequent pRF center modeling can be more accurate by minimizing the influence of surround suppression as well as the influence of other potential artifacts arising in areas distant to the pRF center. We have recently performed a quantitative comparison between our method and several other methods that directly (i.e. before estimating the topography) fit isotropic Gaussian¹, anisotropic Gaussian, and difference of isotropic Gaussians to the pRF⁹. It was found that the topography-based method outperformed these methods with respect to pRF center modeling by achieving higher explained variance of the BOLD signal time series.

Accurate estimation of pRF properties in various areas reveals how they cover the visual field and is important for investigating the functional organization of the visual cortex particularly as it relates to visual perception. Properties such as how pRF size changes with eccentricity^1,10 and pRF center surround organization⁹ are well studied in the human literature. The proposed method for estimating the pRF topography results in more accurate pRF parameter modeling and is more likely to reveal unknown regularities, not easily modeled a-priori in the direct parametric models. This approach will be especially suitable for studying pRF organization in patients with visual pathway lesions, for whom pRF structure is not necessarily predictable a-priori. Below is described how to estimate the pRF topography and how to use the topography to model the pRF center.

Protokół

1. Data Acquisition

1. Prepare a stimulus protocol that is effective in eliciting a reliable retinotopic visual response as previously described in Dumoulin and Wandell¹ and Lee et al.². However, other well established paradigms are also applicable depending on the specific experimental question to be addressed.
2. Present bar stimuli drifting across the screen sequentially along 8 directions of space, in steps of 45 degrees. Ensure that the motion is in synchrony with scanner frame acquisition (TR ~2 sec) so that the bar moves a step once an fMRI frame starts and stays at the new location until the frame ends.
3. To measure a correct baseline signal, add epochs without bar stimulation¹.
   1. Define a field of view (10 to 15° radius) in visual angle over which the stimulus is presented. Present moving or flickering checkerboard patterns (checker size = 0.94 x 0.94 deg², pattern update rate = 250 msec/pattern) within the bar to elicit strong visual responses.
   2. Input the following specific parameters: 8 evenly spaced directions of motion, bar width equal to 1.875 deg, and bars move by half the bar width per frame (2 sec). Additional details can be found in Lee et al.^2.
   3. Generate a spot (~0.25°) in the screen center on which the subject’s eyes fixate during the experiment. Change color of the spot randomly in time.  
4. Scan the brain of a subject in an MRI scanner using a typical echo-planar-imaging (EPI) scan that has 192 frames duration (24 frames in each direction of motion). Repeat the scans 4-8 times to increase signal-to-noise ratio.
5. Set parameters for the EPI sequence as follows: TR = 2 sec, TE = 40 msec, matrix size = 64 x 64, 28 slices, voxel size = 3 x 3 x 3 mm³, flip angle = 90°, Alternatively, apply sequences with a finer resolution (e.g., 2 x 2 x 2 mm³) or a short TR (e.g., 1-1.5 sec) covering only the visual cortex².
6. Track eye movements with an eyetracker system during functional scans to ensure fixation is maintained to within 1-1.5° of the fixation point.
   NOTE: Here, a head-coordinate based eyetracker in a goggle system is used, but other suitable eyetracker systems can be used instead.
7. Instruct the subjects to fixate the spot on the screen center generated in step 1.3.2. To ensure the subjects are fixating, instruct them to report the color changes of the fixation spot.
8. Obtain anatomical scans, at 1 x 1 x 1 mm³ resolution (e.g., T1-MPRAGE; TR = 1,900 msec, TE = 2.26 msec, TI = 900 msec, flip angle = 9°, 176 partitions).
   NOTE: These anatomical scans will be used for segmentation as well as for aligning the functional images to the anatomy both within and across scans. For better alignment between functional (EPI) images and the anatomy, obtain also an inplane anatomy scan, with resolution identical to the EPI, using T1-weighted fast spoiled gradient echo (SPGR) sequence¹.

2. Data Pre-processing

NOTE: Prior to estimating pRF properties, several typical fMRI data pre-processing steps are needed, such as head motion correction and alignment of functional volumes to the anatomical scan. In this article, all pre-processing, estimation, analysis and presentation of results obtained are performed using the open source MATLAB-based software toolbox VISTA LAB available on the VISTA software site. http://white.stanford.edu/newlm/index.php/Main_Page.

1. Load the anatomical scan into MATLAB and prepare a volume anatomy using a function called createVolAnat.
2. Segment Gray matter, White matter, and CSF using the function “ItkGray”.
3. Prepare functional data by converting DICOM (i.e., raw MRI file format for Siemens) files into NIFTI (i.e., standard functional MRI file format) files, and load data into VISTA using a function called mrInit.
4. Correct head-motion and align functional images to the anatomy loaded in step 2.1 using rxAlign based on an affine matrix transformation.
5. Average functional motion-corrected scans for improving signal-to-noise ratio by clicking mrVISTA Analysis TimeSeries Average tSeries. Exclude from averaging scans during which eye movements deviates from fixation more than 1-1.5°. If signals from different runs have different dc-drifts, average functional scans after removing the dc-drifts.
6. Calculate the mapping coordinates between functional scans and Gray matter and identify corresponding Gray-matter voxels in the functional scans by selecting the following menus: mrVISTA Window Open Gray 3-View Window. Assign BOLD signals in the Gray matter voxels by interpolation, choosing one of the options available in mrVISTA.

3. Estimation of pRF Topography and Parametric Modeling

1. Download the code files through the following link: https://sites.google.com/site/leesangkyun/prf/codes.zip, extract the compressed file and place them in a preferred location of the local computer. Add the path of the folder in MATLAB.
2. Set the stimulus parameters used in the experiment by selecting the following menus: mrVISTA Analysis Retinotopic Model Set Parameters. Specify the following parameters such as stimulus images, the stimulus size, the canonical hemodynamic function, the frame rate of the fMRI scanner.
3. Prior to the pRF estimation, prepare the initial parameter sets (Figure 1B).
   1. Set the cross-validation sets in “tprf_set_params.m” from the code files. Divide timeseries into at least two subsets (one set for testing and the remaining sets for training) that are long enough for the bar to sweep the entire stimulus space. Alternatively, without averaging scans in step 2.4, validate scans by leaving out one scan for testing and using the remaining scans for training.
   2. Set a coarse parameter set (λ in Figure 1; λ = [10^-2 10^-1 1 10¹ 10²]) in “tprf_set_params.m”. Then, set a fine scale range ([0.1 0.3 0.5 0.7 0.9 1 3 5 7 9]) in “tprf_set_params.m”.
      NOTE: The program uses the coarse set to select the λ resulting in the highest explained variance. Then, the program searches the space around the selected λ using the fine scale range, further refining the selection of λ that yields the highest explained variance.
   3. Set a threshold (0.2) of the explained variance for visually responsive voxels in “tprf_set_params.m”.
      NOTE: This threshold is used as the reference for selection of visually responsive voxels. Alternatively, make an ROI for a non-visually responsive region (e.g., by drawing a sphere with a radius of 1 cm in a non-visually responsive brain area), where the threshold can be automatically calculated.
   4. Set a set of thresholds ([0.3, 0.5, 0.7]) for defining the pRF center region in the normalized topography in “tprf_set_params.m” (i.e., [0 to 1] or [-1 to 1] with epochs without bar stimulation in step 1.3.1).
      NOTE: From the set of thresholds the program provided selects the “best” threshold, i.e. the threshold that defines a pRF central region for which the pRF center model explains the greatest signal variance. Alternatively, choose a different set of threshold values depending on the characteristics of the topography.
4. Execute “tprf_runpRFest.m” calculate the pRF topography (Figure 1) and fit a 2D anisotropic Gaussian. After specifying all parameters described in this protocol, and running the code, obtain the final estimation results.

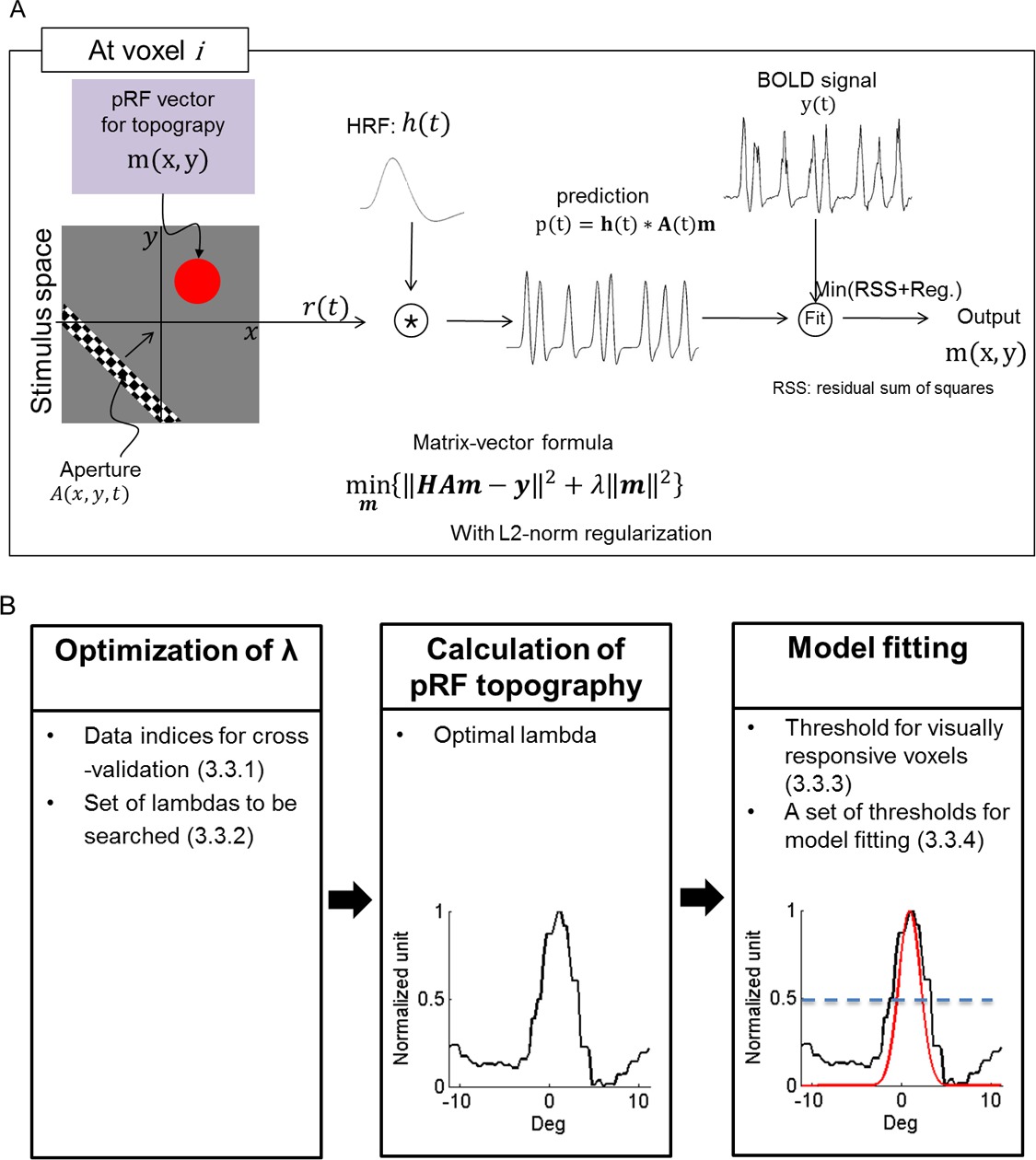
Figure 1: PRF estimation process. (A) Schematic illustration of the process followed for pRF topography estimation. h(t): hemodynamic response function, A(t): stimulus, m: pRF, Reg: L2-norm regularization. (B) Specific steps for pRF topography estimation and pRF center modeling. The set of parameters required for the estimation is listed in each step. A one-dimensional section of topography and its model are illustrated. Under “Model Fitting”, black and red curves represent the topography and its pRF center model with a center threshold of 0.5, respectively. The blue dashed line indicates a threshold for the pRF central region.

Wyniki

Accurate pRF modeling requires capturing pRF shapes correctly. Without knowing the pRF topography, the selection of circularly symmetric models used in prior studies^1,9-11 is a reasonable choice. This is because, if the local retinotopic organization is homogeneous in all directions of visual field, a local population response could be represented as a circularly symmetric cumulative aggregate of neuronal responses. However, our observations demonstrate that this is not necessarily the case (Figure 2

Dyskusje

This article demonstrates how to estimate the topography of visual population receptive fields in human visual cortex and how to use it to select an appropriate parametric model for the receptive field. For a successful retinotopy, an appropriate stimulation protocol and an efficient analysis method should be selected, and the subject’s experimental parameters (motion and fixation) should be optimized. Bar stimuli moving sequentially across the visual field are an efficient stimulus paradigm for pRF estimation as i...

Materiały

Name	Company	Catalog Number	Comments
MRI scanner	Siemens/Philips/GE
MATLAB	The Mathworks, Inc.		http://www.mathworks.com
VISTA software	VISTA software group		http://white.stanford.edu/newlm/index.php/Software
PsychoToolbox	PsychoToolbox		http://psychtoolbox.org
Eye Tracker (VisuaStimDigital)	Resonance Technology Inc		http://mrivideo.com/