Parameterizing V-notch Weir Equations for Flow Monitoring in a Drainage Control Structure

Резюме

This protocol describes methods for obtaining weir flow equation coefficients for a V-notch weir within a drainage control structure using (1) a laboratory calibration procedure and (2) an online tool, the "Weir Flow Equation Coefficients Calculator", developed by the authors. These methods apply to flows contained within the V-notch and overtopping flows.

Аннотация

Accurate estimation of drainage discharge (flow rate or water volume per unit time) is essential for calculating nutrient loads delivered to surface water and assessing the performance of edge-of-field conservation practices. Determining drainage flow rates requires monitoring the head in a drainage control structure and applying an appropriate equation for the weir installed in the structure. Previous studies that developed calibrated equations for weirs in control structures have produced different equations (i.e., different weir flow equation coefficients) for the same type of weir and control structure size. This study describes procedures for setting up experimental water flow rate and head measurements within a drainage control structure and developing a weir equation for flows contained within a V-notch weir. Additionally, the procedure for obtaining a weir equation for overtopping flows -- when the water level exceeds the top of the V-notch weir -- is outlined. This process involves using the weir equation developed in the laboratory for a V-notch weir and an online tool, the "Weir Flow Equation Coefficients Calculator", developed by the authors. The online tool can also generate weir flow equation coefficients for both V-notch-contained and overtopping flows across various sizes of Agri Drain water control structures, even when users lack site-specific flow rate vs. head relationship.

Введение

In evaluating the performance of edge-of-field conservation practices that reduce nutrient loss from subsurface drainage water (saturated buffers, bioreactors, and drainage water management), it is important to accurately determine drainage discharge and nutrient concentrations. Standard methods are readily available for accurately determining nutrient concentrations (e.g., nitrate), such as laboratory methods from water samples¹ or sensors for continuous monitoring of nutrients^2,3. Determination of drainage flow rates in edge-of-field conservation practices, on the other hand, is not as straightforward as with nitrate concentration and usually involves the use of a drainage water level control structure^4,5. A drainage water level control structure is used in an edge-of-field conservation practice with the dual purpose of controlling the upstream water head and monitoring the discharge flow rates with the use of weirs. Important components to consider while determining drainage flow rates include the size of the drainage control structure, the type of weir used in the structure, flow conditions within the structure, accurate measurement of heads, and the use of appropriate weir equations to convert heads to discharge flow rates. While these structures are generally limited to artificially "tile" drained lands, drained agricultural land exceeds 21 million ha in the US⁶ and impacts nutrient loads to streams and rivers⁷.

Determination of flow rates using weirs is a common practice, and standard procedures and calibration equations are available for flows in open channels⁸. However, only a limited number of studies have developed calibration equations for weirs in a drainage control structure^{5,9,10,11,12,13,14,15,16,17}. Chun and Cooke¹⁰ pioneered the development of calibration equations for rectangular weirs for various sizes of control structures. Following Chun and Cooke¹⁰, Christianson et al.⁹ developed a single calibration equation for a 45° V-notch weir in 15 cm (6 in) and 25 cm (10 in) control structures with weirs placed at different heights from the bottom of the structures. Shokrana and Ghane¹⁴ provided a different flow equation for a 45° V-notch weir in a 25 cm (10 in) structure from Christianson et al.⁹, when the weir was placed about 30 cm above the bottom of the structure. The authors attributed the difference in the two calibration equations to the use of a calibrated weighing device for measuring flow rates, suggesting that a unified procedure for obtaining flow rates, heads, and the calibration equations for weirs for flows contained within the V-notch in control structures is lacking.

In our recent study¹¹, we developed calibration equations for 45° V-notch weirs in Agri Drain control structures based on their size (15cm [6 in], 20 cm [8 in], and 30 cm [12 in]) for flows contained within the V-notch and overtopping flows (i.e., when the head exceeds the top of a V-notch weir). While the calibration equation for flows contained within the V-notch is a simple power relationship between head (h) and flow rate (Q, equation 1)^5,9,11,13,14, overtopping flows require the use of a compound weir equation, which is more complicated (i.e., has more terms) because it combines equations for a V-notch weir and a rectangular weir (equation 2)¹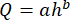¹.

     (1)

where, Q = flow rate, h = head, and a and b = weir coefficients whose values depend on the shape of the weir, the size of the control structure, the flow conditions, and the units for Q and h.

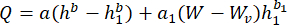     (2)

where, Q = flow rate, h = the total head, h₁ = head above the top of V-notch weir (i.e., in the rectangular weir above the V-notch), W = width of the rectangular weir section above the top of V-notch weir, W_v = top width of the V-notch weir, a and b = weir coefficients for the V-notch weir, and a₁ and b₁ = weir coefficients for the rectangular section above the V-notch weir.

The adoption of a smart drainage system with sensors to monitor and automatically adjust the water levels in a control structure using remotely controlled adjustable gate valves is increasing in edge-of-field conservation practices in the US. Most of these systems, which were originally designed to use only a simple power function, cannot accommodate the compound weir equation (equation 2) for the overtopping flows and demand the development of unique flow equations of the form shown by equation (1) for each drainage control structure for overtopping flows. Additionally, users involved in measuring and monitoring flow rates and nutrient losses may find it cumbersome to use equation (2) for overtopping flows due to the requirement for more parameters. To overcome these challenges, we developed the "Weir Flow Equation Coefficients Calculator" tool. This online tool (available at: https://www.ars.usda.gov/midwest-area/ames/nlae/docs/tools-available-from-nlae/) provides weir flow equation coefficients for standard sizes of drainage control structures (Table 1) for a 45° V-notch weir. More importantly, the tool calculates weir flow equation coefficients for overtopping flow and consists of only two parameters, as presented in equation (1), based on the size and dimensions of the control structure provided by the user. When the appropriate equipment is available to measure site-specific flow rate vs. head relationships, the tool also accepts a calibration equation for flows contained within the V-notch weir as user input and calculates the weir flow equation coefficients for overtopping flows. Thus, this protocol describes the setup for flow measurement in a drainage control structure and a universal method for the development of a site-specific calibration equation. Next, the use of the tool "Weir Flow Equation Coefficients Calculator" for calculating weir flow equation coefficients for flows contained within the V-notch and overtopping flows is described. Finally, monitoring and maintenance of flows in a drainage control structure is described, which will facilitate accurate estimation of drainage flow rates using the weir equations obtained from the tool.

протокол

The details of the consumables and equipment used in this study are listed in the Table of Materials.

1. Obtaining weir flow equation coefficients for flows contained within the V-notch by laboratory calibration in a drainage control structure

1. Setting up the drainage control structure for a calibration experiment
   1. Connect the inlet section of the control structure to the pump assembly (consisting of a pump, a flow meter, and the necessary pipes, fittings, and valves) and the outlet section to the drainage pipe (see Figure 1). Ensure to seal additional outlets from the control structure, if any.
   2. Measure the top width (Wv, Figure 2A) and depth (D, Figure 2B) of the V-notch weir.
   3. Measure the distance (width, W) between the tracks (Figure 3A) where the stoplogs (boards used for maintaining the water level depth in the control structure, Figure 3B) and V-notch weir fit in the drainage control structure.
   4. Insert the stoplogs between the tracks one at a time. Ensure the bottom stoplog sits tightly on the bottom of the control structure so that there is no leakage from beneath the stoplog.
   5. Stack additional stoplogs above the existing ones in the control structure until the desired height is reached. Ensure that the stoplogs are set tightly and no leakage occurs between the stoplogs and the rails.
      ​NOTE: The total height of the stoplogs should be greater than the opening of the inlet pipe and correspond to the design depth of the water table in the saturated buffer, bioreactor, or controlled drainage system. The setup in the laboratory for the calibration experiment should best represent the flow conditions in the field for accurate flow rate estimations.
   6. Place the weir plate firmly above the top stoplog.
   7. Measure the inner height of the control structure (D₁) and the distance between the top of the control structure and the top of the V-notch weir (D₂) using a measuring tape which has its zero-marking flushed with the edge of the tape (see Figure 4A).
   8. Calculate the height of the V-notch crest from the bottom of the control structure (D₃) as: D₃ = D₁- D₂- D, where D is the depth of V-notch obtained from step 1.1.2.
      NOTE: Do not calculate the height of the V-notch crest from the bottom of the control structure as the sum of the heights of stoplogs used as the rubber gasket around the stoplogs increases the combined height of stoplogs.
   9. Firmly connect the manometer tube/stilling well (used for determining the water level in the control structure) to the control structure. Affix a tape measure to the outside wall of the control structure next to the manometer with the "zero" value corresponding to the base of the interior of the control structure (see Figure 4B).
2. Measuring flow rates and head
   1. Start the pump and allow water to fill the inlet chamber and subsequently flow through the weir.
   2. Select a flow rate of about 1-1.5 L.s^-1 (15-25 gpm) by adjusting the valve in the pump assembly and monitoring the display on the flow meter.
   3. Allow sufficient time for the flow to stabilize, usually at least 3 min. The corresponding head should be at least 6 cm (>2.4 in) so that the flow nappe does not stick to the weir plate⁸. Increase the flow rate if the head is less than 6 cm (2.4 in) (Figure 5A).
   4. Once the flow is stable, record the flow rate reading from the display on the flow meter. Take 8-10 consecutive readings within 2 min and calculate the average flow rate (Q) (Figure 5B).
   5. Measure the height of water in the stilling well/manometer tube. If the water level in the stilling well/manometer tube fluctuates, take the readings for the high and low levels of water during a period of at least 30 s and obtain the average value for the height of water above the bottom of the structure (D₄) (Figure 5C).
   6. Calculate the head (h) as: h = D₄- D₃.
   7. Increase the flow rate by approximately 1-1.3 L.s^-1 (15-20 gpm) and wait for the flow rate to stabilize.
   8. Obtain the flow rate and corresponding head as described in steps 1.2.3-1.2.6.
   9. Increase the flow rate at least 5 more times until the water level reaches near the top of the V-notch and repeat procedures 1.2.3-1.2.6 for each increase in the flow rate.
3. Developing the weir calibration equation for flows contained within the V-notch
   1. In an Excel spreadsheet, enter the values of the head (h, cm) and the corresponding flow rates (Q, L.s^-1) through the V-notch weir.
      NOTE: An Excel spreadsheet consisting of measured flow rates and heads in a 20 cm (8 in) control structure is provided as Supplementary File 1.
   2. Plot the measured flow rates (Q, Y-axis) against the measured head (h, X-axis) and fit a power function as in equation (1). Select the data range in the spreadsheet, then click Insert > Charts > Scatter. Right-click on the data points in the chart, then click Add Trendline > Power > Display Equation on chart > Display R-squared value on chart.
   3. Check the goodness-of-fit of the power function both visually and by using R² value (Figure 6). This is the weir equation for flow contained within V-notch for the control structure.

2. Using "Weir Flow Equation Coefficient Calculator" for obtaining weir coefficients for flows contained within the V-notch and overtopping flows

NOTE: The following steps require the use of the "Weir Flow Equation Coefficient Calculator" tool available at https://www.ars.usda.gov/midwest-area/ames/nlae/docs/tools-available-from-nlae/. 

1. Weir flow equation coefficients for overtopping flows using own calibration equation
   1. Open the link https://www.ars.usda.gov/midwest-area/ames/nlae/docs/tools-available-from-nlae/ and click on “Weir Flow Equation Coefficients Calculator” on the webpage. This step will open the tool in a new browser (Supplementary Figure 1).
   2. Select the unit between Metric (SI) and US Customary units using the radio buttons (Supplementary Figure 2).
   3. In the section Size of control structure, leave the selection to the default value of 6-in (15-cm) as the user provides their own weir equation coefficients.
   4. Click on Yes as the response to "Do you have your own calibration equation?" and enter the values of the parameters a and b corresponding to the equation for flows contained within the V-notch, Q = ah^b and obtained from step 1.3.2 (Supplementary Figure 2).
   5. Enter the values of the weir specifications in the Inputs section of the tool. The inputs include the width between the tracks (W), depth of V-notch (D), and width of V-top (W_v). Refer to the figure on the right for the symbols (Supplementary Figure 2).
   6. Get the values of coefficients for overtopping flows from the table Coefficients for V-notch weir equation, Q = ah^b, and the plot of flow rate against the head from the Results section of the tool (Supplementary Figure 2).
2. Weir flow equation coefficients for flows contained within the V-notch and overtopping flows using the tool
   1. Open the tool as described in section 2.1.1. and select the unit and the size of the control structure using the radio buttons (Supplementary Figure 3).
   2. Click on No as the response to "Do you have your own calibration equation?"
   3. Enter the values of the weir specifications as described in section 2.1.5.
   4. Get the values of the coefficients for flows with V-notch weir, and overtopping flows from the table and the plot of flow rate vs. flow depth relative to the V-notch crest from the Results section of the tool (Supplementary Figure 3).

3. Flow monitoring and maintenance in drainage control structures

1. Verification of water levels in a drainage control structure
   NOTE: Ensuring that the flow levels obtained from the sensors are correct is crucial for accurate estimation of flow rates, which is achieved by comparing sensor readings with manual measurements through regular field visits.
   1. Using a tape measure, measure the distance of the water level from the top of the control structure in the inlet chamber near the location of the sensor within the chamber.
   2. To take the measurement, lower the tape measure into the control structure until it just touches the meniscus of the water level. Take this measurement 1-3 times and record the distance.
   3. To obtain the record of the sensor reading, open the control panel box and record the number corresponding to the water level reading (Figure 7).
      NOTE: Depending on the settings of the control panel, the screen may display the water level measurement from the top or the bottom of the drainage control structure.
   4. To compare the manual measurement with the sensor reading corresponding to a value of water depth from the bottom of the control structure, subtract your manual measurement from the interior height of the control structure and compare it with the sensor reading.
   5. If there is a discrepancy between the measured and sensor values, check for sources of errors, including the presence of sediments/debris within the control structure, unaccounted changes in weir height resulting from weir management, dislocation of the sensors, and malfunctioning of the sensors and correct accordingly.
2. Obtaining time series of flow rates
   NOTE: A spreadsheet consisting of example data from a saturated buffer site (BC-2)¹⁸ and the procedure for obtaining time series of flow rates using the weir equation coefficients from the tool is described in sections 2.2.1-2.2.4, and is presented in Supplementary File 2.
   1. Download the time series of flow level data from the respective datalogger or server associated with the drainage system.
   2. Using the time series flow level data, calculate the head.
   3. Determine the flow condition, i.e., flow contained within the V-notch (h ≤ D) or overtopping flow (h > D) by comparing head (h) with the depth of V-notch (D) for each time record.
   4. Calculate the drainage flow rate for the flow condition using the weir equation (1) with weir flow equation coefficients obtained from the "Weir Flow Equation Coefficient Calculator" tool (as described in section 2.1. or 2.2.).
   5. In an edge-of-field conservation practice equipped with a smart drainage system, get the time series of flow rates directly from the dashboard of the respective website (Figure 8).

Результаты

The calibration of a stainless-steel 45° V-notch weir was performed in 15 cm (6 in), 20 cm (8 in), and 30 cm (12 in) Agri Drain control structures for flows contained within the V-notch¹¹. The measured values of flow rates and heads and the weir equations obtained by fitting a power function (equation 1) to the measured data for flows contained within the V-notch, as described in the protocol, are presented in Figure 9A-C...

Обсуждение

The protocol (step 1) describes a method for developing a calibration equation for a 45° V-notch weir in an Agri Drain drainage control structure. However, the method can be adapted for developing calibration equations for different types of weirs, such as a rectangular weir, a trapezoidal weir, or a V-notch weir with various angles in any drainage control structure. During the calibration procedure, it is particularly important that accurate heads are obtained, especially at greater flow rates when the water level ...

Материалы

Name	Company	Catalog Number	Comments
Flow meter	Banjo Corp	MFM300	Electromagnetic flowmeter, accuracy within ± 2-3% for flow rates between 0.88 and 42.3 L.s-1 (14 to 670 gpm), and operating temperature range of -12 to 54 °C
Pipe and fittings	N/A	N/A	The pipe length and fittings should be as necessary but fulfill the miniumum straigth pipe requirements for upstream and downstream of flow meter according to manufacturer's recommendation.
Pump	US Motors	15706017-100	Model 15411 60 HP 3 Phase VFD driven
Stoplogs	Agri Drain	700320 (5 in. stoplog), 700321 (7 in. stoplog), 700333 (7 in. bottom stoplog with bottom gasket)	Three types of PVC stoplogs of heights 5 inch, 7 inch, and 7 inch bottom stoplog with bottom gasket
Tape Measure	Stanley PowerLock	33-158	5m/16' tape measure
V-notch weir	Agri Drain	701132	Stainless steel 45° (3 mm thickness, V-notch depth of 17.145 cm) notched weir with PVC carrier (13 mm thickness)
Water Level Drainage Control Structure	Agri Drain	3CINLINE06X08PVC	A 3-chambered inline water level control structure with nominal size of 20.32 cm (8 inch) and V-notch weir present in the first gate (Stoplogs included in purchase)