In the early 17th century, German astronomer and mathematician Johannes Kepler postulated three laws for the motion of planets in the solar system. He formulated his first two laws based on the observations of his forebears, Nikolaus Copernicus and Tycho Brahe.
Polish astronomer Nikolaus Copernicus put forth a theory that stated a heliocentric model for the solar system. According to this heliocentric theory, all the planets, including Earth, orbit the Sun in circular orbits.
On the other hand, Danish astronomer Tycho Brahe, the employer of Johannes Kepler, had meticulously recorded the position of every planet in detail. For most visible planets, these observations were in accordance with the Copernican heliocentric theory, except for the planet Mars.
While analyzing the Mars data of Tycho Brahe, Johannes Kepler realized that the Copernican theory was accurate except that planets revolve around the Sun in an elliptical orbit rather than circular orbits. This led him to his first law of planetary motion, which states that every planet travels along an ellipse, with the Sun located at one of the ellipse's foci.
An ellipse is an elongated circle. The degree of elongation of an ellipse is expressed using a parameter called eccentricity.

An axis of an ellipse along the elongation is called the major axis a, and the one perpendicular to it is the minor axis b. Therefore, the eccentricity of an ellipse is expressed as
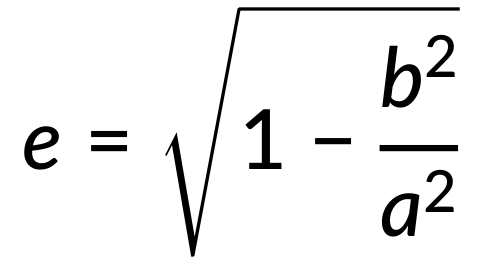
Since b < a, the eccentricity of an ellipse is always less than unity. For a circle, a = b, hence the eccentricity of a circle is zero.
The eccentricity of Martian orbit is 0.0935. It is considered to have the most eccentric orbit after Mercury, whose eccentricity is 0.21. Earth's orbit has an eccentricity of 0.0167.
Since planets are in elliptical orbits with the Sun at one of the foci, their radial distances change throughout the year. Their closest distance from the Sun is known as the perigee, while the farther distance is called the apogee.
This text is adapted from Openstax, University Physics Volume 1, Section 13.5 Kepler's Laws of Motion.
Del capítulo 14:

Now Playing
14.15 : Primera ley de Kepler sobre el movimiento planetario
Gravitación
3.7K Vistas

14.1 : Gravitación
Gravitación
6.0K Vistas

14.2 : Ley de la gravitación de Newton
Gravitación
10.4K Vistas

14.3 : Gravitación entre masas esféricamente simétricas
Gravitación
788 Vistas

14.4 : Gravedad entre cuerpos esféricos
Gravitación
8.0K Vistas

14.5 : Coordenadas de masa reducida: problema aislado de dos cuerpos
Gravitación
1.1K Vistas

14.6 : Aceleración debida a la gravedad en la Tierra
Gravitación
10.3K Vistas

14.7 : Aceleración debida a la gravedad en otros planetas
Gravitación
4.0K Vistas

14.8 : Peso aparente y la rotación de la Tierra
Gravitación
3.5K Vistas

14.9 : Variación en la aceleración debida a la gravedad cerca de la superficie terrestre
Gravitación
2.3K Vistas

14.10 : Energía potencial debida a la gravitación
Gravitación
3.7K Vistas

14.11 : El principio de superposición y el campo gravitatorio
Gravitación
1.1K Vistas

14.12 : Velocidad de escape
Gravitación
3.6K Vistas

14.13 : Órbitas circulares y velocidad crítica para satélites
Gravitación
2.8K Vistas

14.14 : Energía de un satélite en una órbita circular
Gravitación
2.1K Vistas
See More
ACERCA DE JoVE
Copyright © 2025 MyJoVE Corporation. Todos los derechos reservados