Method Article
Measuring Spatially- and Directionally-varying Light Scattering from Biological Material
In This Article
Summary
We present a non-destructive method for sampling spatial variation in the direction of light scattered from structurally complex materials. By keeping the material intact, we preserve gross-scale scattering behavior, while concurrently capturing fine-scale directional contributions with high-resolution imaging. Results are visualized in software at biologically-relevant positions and scales.
Abstract
Light interacts with an organism's integument on a variety of spatial scales. For example in an iridescent bird: nano-scale structures produce color; the milli-scale structure of barbs and barbules largely determines the directional pattern of reflected light; and through the macro-scale spatial structure of overlapping, curved feathers, these directional effects create the visual texture. Milli-scale and macro-scale effects determine where on the organism's body, and from what viewpoints and under what illumination, the iridescent colors are seen. Thus, the highly directional flash of brilliant color from the iridescent throat of a hummingbird is inadequately explained by its nano-scale structure alone and questions remain. From a given observation point, which milli-scale elements of the feather are oriented to reflect strongly? Do some species produce broader "windows" for observation of iridescence than others? These and similar questions may be asked about any organisms that have evolved a particular surface appearance for signaling, camouflage, or other reasons.
In order to study the directional patterns of light scattering from feathers, and their relationship to the bird's milli-scale morphology, we developed a protocol for measuring light scattered from biological materials using many high-resolution photographs taken with varying illumination and viewing directions. Since we measure scattered light as a function of direction, we can observe the characteristic features in the directional distribution of light scattered from that particular feather, and because barbs and barbules are resolved in our images, we can clearly attribute the directional features to these different milli-scale structures. Keeping the specimen intact preserves the gross-scale scattering behavior seen in nature. The method described here presents a generalized protocol for analyzing spatially- and directionally-varying light scattering from complex biological materials at multiple structural scales.
Introduction
The color and pattern of an organism's integument play ecologically and socially critical functions in most animal taxa. These phenotypic properties are determined by the interaction of light with the structure of the integument, which can exhibit optical scattering that varies both spatially (across the surface of the integument) and directionally (with change in lighting and viewing direction). In complex biological materials, such as feathers, the direction of light scattering is influenced by the orientation of repeating milli-scale geometry. These milli-scale structures themselves may be embedded with nano-scale structures, such as melanin arrays, which often inherit the milli-scale orientation. From nano- to macro-scales, the structure of the integument has evolved functionally to increase the signaling capability of the organism. In order to assess the influence of the morphology of different scales upon the overall appearance, tools to measure and analyze the color of biological structures need flexibility to isolate directional light scattering at various scales of magnification.
We developed image-based measurement tools to study how the performance of a feather's complex and varied milli-scale morphology (barb rami, distal barbules, and proximal barbules) expands the range of expression possible from nano-scale structures alone. In a single image recorded by the camera, we observed that light reflected differently at different locations on the surface of the feather, that is, light reflectance was spatially-varying. When we moved the light and camera direction with respect to the feather, we observed the reflectance changed, that is, light reflectance was directionally-varying1. Following these observations, we designed a protocol to methodically move the light and camera around the subject using a spherical gantry2,3, with which we captured 2 dimensions of surface position (X and Y), 2 dimensions of light direction (latitude and longitude), and 2 dimensions of camera direction (latitude and longitude) (Figure 2). In software we visually explored the 6 dimensions of the scattered light as a function of position, illumination direction and view direction.
Previous research into the reflectance from integuments has too frequently discounted the contribution of directionality -- e.g. diffuse vs. specular or isotropic vs. anisotropic reflection -- to color expression. Most color measurements have fixed the incident light, object, and viewing geometry to carefully avoid directional effects. For instance, to eliminate specular reflection from color measurements, it is common to place the light normal to the surface and record the reflectance at 45° from the normal. Studies that do link morphology to directionally-varying reflectance typically focus on the nano-scale and its iridescent consequences4-8. Few consider the contribution of micro-, milli-, and macro-scale geometries to the far-field optical signature8-11. It is therefore common to employ a light detector to aggregate reflectance across a single area of interest that may include multiple milli- and/or macro-scale components, such as barb rami, barbules, and even entire feathers6,8,11-17. When the region of interest is either smaller than the resolution limit of the detector or does not conform to the shape of the detector's field of view, the common protocol specifies specimen dissection to isolate the light scattering from the specific milli-scale element8,10,13,15.
We have developed a more encompassing protocol for measurement acquisition and visualization that encourages exploration of the many variables often ignored in other more focused studies. We measure light scattering over a sphere of directions and across a region of space using a massive set of high-dynamic range, high-resolution photographs taken from a systematic set of light and viewing directions. We employ a high-resolution imaging sensor with its 2D array of fine-scale pixel detectors. Aggregation in hardware occurs at the pixel-level, at a scale smaller than the milli-scale elements we are measuring. A second stage aggregates individual pixels in software as the user selects the shape and size of the region of interest. Accordingly, a single measurement set can be repeatedly analyzed in software to explore different aspects of light interaction with material at multiple biologically-relevant positions and scales. By eliminating dissection and measuring the entire feather, our protocol has the advantage of leaving the morphology of the feather vane intact, retaining natural context and function that is, light's interactions between constituent milli-scale elements.
Light scattering from organismal structure is multidimensional and difficult to quantify. Measured 6D light scattering cannot as yet be attributed to specific morphology within a hierarchy of scale with any singular instrument. But we have made an important step in this pursuit. We have developed a tool encompassing three complementary methods -- sampling reflectance using the gantry, exploring large data volumes in software, and visualizing data subsets graphically -- to extend our ability to measure 6D light scattering at any point on a material, down to the milli-scale. As protocols such as ours are employed, we predict biologists will identify a myriad of directionally- and spatially-varying traits and corresponding structural adaptations at multiple scales of development. Using our tools we are engaged in characterizing the signaling potential of the directional and spatial expression of milli-scale structures, and hope to shed light on their adaptive consequences. We address a range of questions, such as: from any given observation point, which fine-scale elements or gross-scale regions of the feather reflect strongly? How does the orientation of the fine-scale elements influence the direction of scattered light? What morphological conditions produce a satiny gloss vs. a sequined sparkle of the iridescent ornament? Do some species produce broader "windows" for observation of iridescence than others? These questions may be asked about birds and their feathers but also about any other organisms that have evolved a particular surface appearance for signaling, camouflage, or other reasons.
Protocol
When using our methods to measure a sample, the experimenter must decide on a set of camera and light directions, and for each combination of camera and light directions, the camera makes several exposures with different shutter speeds. Moving the camera requires additional processing, because it changes the view of the sample as seen in the image, so we normally use a small number of camera directions and a larger number of light source directions.
In the detailed protocols below, we first describe how to perform a measurement with many light source directions and a single camera direction, and how to process and visualize the resulting data (Protocol 1). In the primary protocol, which can be used by itself when a single view is sufficient to observe the phenomena being studied, we always keep the camera view perpendicular to the sample (Primary Routine in Figure 1). When multiple camera directions are required, the resulting oblique views of the sample can be warped to undo the effects of moving the camera and thereby to align the images exactly with the canonical perpendicular view. To compute these warps, we perform additional calibration steps that use observations of targets placed around the sample to precisely determine the motion of the camera relative to the sample. Protocol 2 details this calibration procedure and explains how to select parameters and run Protocol 1 multiple times to gather data from multiple views (Secondary Routines in Figure 1). Finally, Protocol 3 details the additional steps that must be inserted into Protocol 1 to rectify the oblique views during data processing.
1. Measure Scattered Light in the Direction of the Surface Normal over the Sphere of Incident Directions (Primary Routine in Figure 1)
- Prepare and Mount the Object to be Measured
- Prepare a thin ferrous metal mounting plate with a ½-inch aperture surrounded by a ring of targets (as seen in Figure 2).
- Prepare the material to be measured. If measuring a feather, groom the barbs to correct for any unzipped or misaligned sections of the pennaceous vane.
- Lay the surface of the object (obverse face of the feather) against the back side (opposite the target ring) of the plate.
- Center the region of interest over the ½-inch aperture in the plate.
- Lay a sheet of magnetic film with a 5/8-inch aperture against the back side of the object (reverse face of the feather), thereby pressing the object flat against the plate.
- Align the aperture of the film to the aperture of the plate without shearing the surface. The flattened surface, pinned around the circumference of the circular aperture, yields a planar macro-surface approximately coincident with the plate's surface.
- Configure the Gantry
- Locate the center of the circular aperture at the origin of the gantry coordinate system.
- Place a light source on the gantry outer arm. Aim and narrowly focus the light at the object, ensuring that the aperture is uniformly illuminated for all light source angles.
- Place a camera on the gantry inner arm. Adjust the camera distance and the focal length of the macro lens until the ring of targets fills the width of the sensor.
- Calibrate the rotational movements (θ,φ) of the camera and lamp arms. Calibrate the inclination (θ) with respect to the object's surface normal so that the camera and the lamp are aligned with the surface normal when θ = 0. Calibrate the azimuth (φ) of the camera to the azimuth of the lamp. The absolute azimuthal orientation is not critical since the captured images may be rotated later in the protocol.
- Configure the Camera Focus and Exposure
- Rotate the camera until the object is viewed at a grazing angle. Decrease the f-number to minimize the depth of field (DOF), then set the focus plane at the center of the aperture. Increase the f-number to increase the DOF until the ring of targets surrounding the aperture is in focus. A compromise between diffraction and DOF-induced blur may be required.
- Clip a color standard flat against the mounting plate. For RGB images use a Macbeth Color Checker. For UV-visible-NIR measurements use Spectralon.
- Photograph the color standard in RAW format. Calculate the color channel multipliers to white balance the image.
- Find the exposure bracket that spans the dynamic range of the scene under the most extreme viewing and lighting directions.
- For each exposure time in the bracket, acquire a dark noise image by exposing the sensor with the lens cap on.
- Acquire Measurements from a Sparsely Sampled Sphere of Incident Directions
- Position the camera axis normal to the surface plane {θ,φ}={0,0}.
- Step the light through of a series of uniformly distributed positions on the sphere, using a coarse sampling (e.g. less than 500 points).
- For each incident light direction in the sampling:
- Capture a raw image for each exposure time in the exposure bracket.
- Capture a single image illuminated by the camera mounted flash synchronized to a relatively short exposure time to suppress the gantry lamp illumination.
- Advance to the next incident light direction and repeat.
- Process Measurements from Sparsely Sampled Sphere
- Using the debug (document) mode of dcrawa to disable its demosaicing function, convert from RAW format to greyscale, 16-bit, linear, PGM format:
- Each dark noise exposure.
- Each exposure of the object at each incident light direction.
- Integrate all low dynamic range (LDR) greyscale exposures under gantry lamp illumination into a single high dynamic range (HDR) color image for each incident light direction.
- Subtract the corresponding dark noise image from each LDR exposure.
- Demosaic each LDR exposure to yield a one-quarter scale image.
- White balance each LDR exposure using the color channel multipliers computed in step 1.C.3.
- Merge dark-noise-subtracted LDR exposures into a single HDR image by summing all the values at each pixel position and dividing by the sum of the exposure times, omitting overexposed pixels from both sums.
- Store HDR image in EXR format encoded in half-float precision and lossless wavelet (PIZ) compression.
- If the camera direction is not the canonical direction or the measurement run is part of a multiple camera direction set (Secondary Routines in Figure 1 and Protocol 2):
- Convert the single LDR greyscale exposure of the flash-illuminated tracking targets for each incident light direction to a demosaiced, one-quarter scale, LDR color image in EXR format.
- Follow Protocol 3 to use the flash-illuminated image to projective transform each HDR lamp-illuminated image into the canonical view.
- Rotate the HDR images into the desired orientation -- e.g. in our case a 90° rotation orients the rachis vertically and the feather tip up.
- Crop the HDR images tightly around the circular aperture. Masking the targets and metal plate outside the aperture reduces file size by up to 25%.
- Permute the data in the entire set of HDR images to create a set of files, one for each of several blocks in the image, that contain all the directional reflectance values organized by pixel. These directional reflectance cache files are organized to enable quick access to all the directional color measurements at a single pixel position of the 2D projection of the 3D object.
- Using the debug (document) mode of dcrawa to disable its demosaicing function, convert from RAW format to greyscale, 16-bit, linear, PGM format:
- Visualize Spatially-varying Light Scattering Across a Hierarchy of Scale
- To browse the measurements, use the custom SimpleBrowser application to interpret the data processed in step 1.E. SimpleBrowser opens to a window containing the image of the feather illuminated by the first incident lighting direction.
- On the image of the feather vane, individual pixels or groups of pixels in linear or rectangular arrangements may be selected (Figure 3). Proceed by selecting a rectangular region of the feather vane for analysis. Then, plot the average directional light scattering from the selected region. A plot window showing reflectance as a function of direction cosines opens adjacent to the image window (R1 in Figure 4).
- By default, the direction of maximum luminance (a transmittance direction in a typical feather measurement) is assigned an exposure of 1. Decrease or increase the exposure in one-half stop (√2 x) increments to adjust the exposure of the reflectance color map.
- Cycle the reflectance color map between luminance, RGB, and chromaticity (See R1, R2, and R3 in Figure 4). For the following steps use RGB.
- To rotate the sphere, click on it to enable the trackball interface. Drag the interface to cause rotation. To view the reflectance hemisphere, return the sphere to its default position (See R2 in Figure 4). Rotate the sphere 180° from its default position to view the transmittance hemisphere (See T2 in Figure 4).
- For another view of the data, select the polar plot mode to scale the radii of each direction on the unit sphere by their respective luminance values. Change the color map of the luminance scaled sphere from RGB to chromaticity (See P3, F3, S3, A3 in Figure 4).
- The illumination direction of the displayed image is circled in red in the directional scattering plot (Figure 4). Click any other incident lighting direction to show the image of the feather illuminated from that direction.
- Decrease or increase the exposure of the image to reveal over and underexposed regions.
- To investigate reflectance across a hierarchy of scales, restore the plot mode to the unit sphere and the color map to RGB. In review, this plot displays the average directional reflectance from the selected rectangular region on the image.
- Change the selection type from rectangular to linear (Figure 3). This will allow study of the directional reflectance from individual fine-scale structures in the rectangular region.
- Plot the reflectance of the linear average in a new window while maintaining the rectangular average for reference. Adjust exposure and set color map to RGB.
- In the linear average plot, the distal barbules spanned by the linear region are seen to reflect light in directions horizontal (Figure 8). Select one of the illumination directions in the linear plot to display the highly reflective distal barbules in the image on the left.
- Step the line towards the tip of the feather until it reaches the region of the feather where the proximal barbules branch from the adjacent rami. In the linear average plot the proximal barbules are seen to reflect light in directions vertical (Figure 8). Select one of the directions to display the highly reflective proximal barbules in the image on the left.
- In the linear plot, observe the fine-scale structures that reflect light in directions horizontal and vertical combine to produce the far-field signal seen in the rectangular plot.
2. Measure Scattered Light in Multiple Camera Directions (Secondary Routines in Figure 1)
Multiple camera views and non-uniform directional sampling allow us to study particular features of the directional reflectance. With the addition of calibration Steps 2.A and 2.B, Protocol 1 has been expanded to handle multiple camera views. Two specific examples graphically illustrated as Secondary Routines II.A and II.B in Figure 1 are set forward in Steps 2.C and 2.D below. In such cases, the camera direction is altered from its canonical direction (normal to the surface), meaning that the object is photographed from a direction inclined from its surface normal. Since images must be mapped into the same coordinate system, we rectify and warp each photograph to match the canonical orientation by referencing the flash-photographed targets surrounding the sample (Figure 9).
- Calibrate Camera Projection and Position:
The purpose of these steps are to calculate the camera projection and position used in image transformation.- Clip a checker-patterned calibration target flat against the mounting plate.
- Capture one image at the canonical camera view (i.e. {θ,φ}={0,0}) and several images at various other camera views spread over a 120° cone centered on the canonical view.
- Load the images into the Bouguet Toolboxb, a MATLAB camera calibration toolkit. Extract the grid corners in each of the images to reconstruct the camera matrices. Export the intrinsic camera projection matrix (P) and the extrinsic camera position matrix (M). The intrinsic camera projection is composed of the focal length and the principal point. The extrinsic camera position is composed primarily of a translation; it translates the origin of the world to the camera position.
- Solve for the matrix that transforms calibration-target coordinates to gantry turntable coordinates (X), i.e. Bouguet space to gantry space.
- Unclip the checker pattern from the metal plate.
- Calibrate Target Positions and Projection Offsets:
The purpose of these steps is to calculate the offsets between the calibration plane, the target plane, and the sample, and to locate the target positions.- Rotate the camera in gantry coordinates so that the optical axis is perpendicular to the surface plane, i.e. the canonical frame.
- Capture an image of the ring of targets surrounding the aperture with flash illumination. This is the canonical image for image alignment.
- Process the raw camera output (Protocol outlined in steps 1.E.3.a. and 1.E.4.).
- Mask the region inside and outside the ring target zone, eliminating stray specular highlights that may confuse target recognition, then find the targets in the image.
- Rotate the camera to a grazing angle and capture an image.
- Calculate the canonical camera pose (Mc= M * Rc) and the grazing angle camera pose (Mg= M * Rg) based on the extrinsic camera matrix M in step 2.A.3. which includes a translation based on the position of the Bouguet checker pattern.
- Redefine M by offsetting its translation by the thickness of the paper target-ring. Iterate by trial and error (recalculating M using a different offset for the calibration plane) until the offset in gantry space between the plane of the Bouguet checkerboard and the plane of the ring of targets, i.e. thickness of the paper target-ring, has been solved. Verify the offset in each iteration by reprojecting the targets in the grazing angle image onto the targets of the canonical image.
- Redefine M following the procedure of the previous step to reproject the apertured object in the grazing angle image onto the apertured object in the canonical image by trial and error until the offset in gantry space between the plane of the ring of targets and the plane of the apertured object, i.e. thickness of the metal plate, has been solved.
- Measure Seven Non-uniformly Sampled Reflectance Hemispheres (Secondary Routine II.A in Figure 1)
- Examine the directional distribution of the reflected light measured from the camera view normal to the surface, i.e. {θ, φ}={0,0} as described in Protocol 1. Resample the reflectance hemisphere to record camera radiance from non-specular directions more sparsely and specular directions more densely.
- Apply the same criteria to sample the reflectance in 6 additional camera directions uniformly distributed over half a hemisphere, i.e. {θ, φ}={30,0}, {30,90}, {60,0}, {60,45}, {60,90}, {60,135}. Predict the specular regions of the 6 additional runs from the viewing direction of each coupled with the reflection angle of the initial run.
- For each of the 7 non-uniformly sampled hemispheres, acquire and process measurements following the instructions in steps 1.D. and 1.E. above.
- Visually browse the directional reflectance from the same region of the feather in each of the 7 non-uniformly sampled hemispheres, following the instructions in step 1.F. above. Arrange the directional reflectance plots for each of the 7 camera directions on a polar coordinate system, where the placement of each plot is based on its camera direction (See the visual results of Routine II.A in Figure 1; also Figure 5).
- Measure finely-sampled semicircular paths to acquire detailed information about color change with angle (Secondary Routine II.B in Figure 1)
- Launch the SimpleBrowser application and input the processed measurements of the non-uniformly sampled reflectance hemisphere with camera direction {θ,φ}={0,0} as described in Step 2.C.1. Select one pixel in the image, then fit a plane to the 90th percentile of the luminance of the hemispherical reflectance at the selected pixel position.
- Construct a 1D acquisition run which finely samples specular reflectance in the specular plane. Generate gantry arm angles in ½° half-angle increments in the plane defined in the previous step. Start with the half-angle equal to 0° and increase the half-angle to 90°. For each measurement in the acquisition run, keep the half-vector constant and equal to the surface normal so that each camera direction is located in the specular direction.
- Acquire and process measurements following the instructions in steps 1.D. and 1.E. above.
- Visually browse the 1D directional reflectance following the instructions in step 1.F., while sampling a very small region (e.g. 3x3 pixels) centered on the same pixel used to fit the specular plane in step 2.D.1. Find the direction of peak reflectance, i.e. shading normal. Construct 3 additional acquisition runs in the same manner as step 2.D.2., but set the half-vector to the shading normal rather than the surface normal. For the 3 additional runs, generate gantry arm angles that lie in planes containing the shading normal but which are rotated 45°, 90°, and 135° with respect to the specular plane defined in step 2.D.1.
- Acquire and process measurements following the instructions in steps 1.D. and 1.E. above.
- Visually browse the 1D directional reflectance following the instructions in step 1.F., while sampling a very small region (e.g. 3x3 pixels) centered on the pixel used to fit the specular plane in step 2.D.1. Export from SimpleBrowser the average reflected radiance of this very small region.
- In MATLAB, plot its chromaticity as a function of half-angle on a chromaticity diagram (Figure 6). Plot its hue, chroma, and luminance as a function of the half-angle (Figure 7).
- Construct four more 1D acquisition runs in the same four planes as above, but this time configure the light and camera directions to measure the width and decay of the specular reflectance. Set the half-angle between the light and camera to a constant 10°. Generate gantry arm angles in 1° half-vector increments around the axis orthogonal to the plane. Start with a half-vector equal to -80° and increase the half-vector to +80°, where 0° equals the shading normal. Note that not all camera directions are located in the specular direction.
- Acquire, process and export measurements following the instructions in steps 1.D. and 1.E., and 2.D.6. respectively.
- In MATLAB, plot its chromaticity on a chromaticity diagram as a function of the angle between the half-vector and the shading normal. Plot its hue, chroma, and luminance as a function of the angle between the half-vector and the shading normal.
3. Projective Transformation
Projective transform each HDR image into the canonical view or the view direction orthogonal to the surface plane. This protocol is accessed by Step 1.E.3.b when a measurement run is part of a multiple camera direction set, such as the examples outlined in Protocol 2 and graphically illustrated as Secondary Routines in Figure 1.
- Read a canonical image illuminated from a non-specular direction. (At grazing specular directions the diminished contrast between the white surface of the paper and the black ink can lead to target detection failure. Compare the clarity of image A and B in Figure 9.)
- Locate the coordinates of the center of each target in the canonical image.
- Load the target image illuminated by camera-mounted flash for a given lamp-camera directional pair (B in Figure 9).
- Roughly transform the target image into the canonical camera frame using the gantry camera matrix M computed in step 2.B.7.
- Locate the coordinates of the center of each target in the transformed target image (C in Figure 9).
- Match each target in the transformed target image to its reference target in the canonical image by finding the minimum distance between image and reference targets.
- Discard any blurred targets caused by DOF at grazing angles (D in Figure 9).
- Solve the 2D projective transform that maps image targets in the canonical frame to canonical-image targets in the same frame.
- Untransform the warped-to-fit targets from the canonical image frame back to the original image frame through the plane of the apertured object (M in step 2.B.8.) rather than the plane of the targets (M in step 2.B.7.).
- Save the target coordinate pairs that map the apertured object in the target image to the apertured object in the canonical target image.
- Load the HDR image illuminated by the lamp (A in Figure 9).
- Infer a spatial projective transform from saved target coordinate pairs to transform the HDR image into the canonical frame (E in Figure 9).
- Return to the main protocol.
a Dcraw is an open-source computer program developed by David Coffin. It converts a camera's proprietary RAW-formatted image (i.e. unprocessed CCD data) to a standard image format. See http://www.cybercom.net/~dcoffin/dcraw/.
b Bouguet Toolbox is a camera calibration toolbox for MATLAB developed by Jean-Yves Bouguet. See http://www.vision.caltech.edu/bouguetj/calib_doc.
Results
The primary measurement of our protocol (Routine I in Figure 1) fixed the camera direction normal to the surface and only moved the light. Since light scattering adheres to the principle of reciprocity, the result is the same whether we hold the camera constant while moving the light over the hemisphere or vice versa. When we fix either the camera or the light, the complete 4-dimensional direction set is undersampled. A fuller picture of the scattering behavior is observed when, unlike the primary measurement, both light and camera are moved away from the surface normal and in a multiplicity of directions. Ideally, we could measure light scattering from many camera directions, even as many as the number of incident light directions, to yield a symmetrical data set. In practice, this would require far too many exposures. In our experience, we can obtain sufficient information about different viewing positions by moving the camera a few times assuming 180° rotational symmetry about the surface normal. During the secondary measurement phase, we acquired measurements from 7 viewing directions distributed over the hemisphere and within 60° of the zenith18,19 (Routine II.A in Figure 1).
In the figures of this paper, we show representative data measured from a feather of Lamprotornis purpureus (Purple Glossy Starling), the reflectance of which is iridescent, glossy, and anisotropic (Figure 5). In each of the 7 viewing directions, reflected light is gathered from hundreds of incident lighting directions on the hemisphere. The directions form a narrow band orthogonally oriented to the central axis of the feather (see feather image in Figure 4). The iridescence color shift is subtle (bluish-green at normal incidence and greenish-blue at grazing incidence) when the feather is viewed normal to its surface as seen in the {0°,0°} RGB plot of Figure 5. As the viewing angle approaches grazing, the angles between the viewing direction and the grazing incident directions are maximized, leading to a more striking color shift (bluish-green at 0° and magenta at 240° between incident and viewing directions) as seen in the {60°,0°} RGB plot in Figure 5.
We can afford to step the light and camera at much finer angular resolution when we restrict the movements to 1 dimension. Figure 6 shows the chromaticity of the reflectance of L. purpureus plumage as a function of the angle between the incident and viewing directions, where the incident and viewing directions are in the plane containing the specular band, which is perpendicular to the longitudinal axis of the distal barbule. As the iridescent color arcs through chromaticity space, the hue shifts from bluish-green to purple.
Spatial variation in the directional reflectance is visible where different (X,Y) coordinates of the integument correspond to different milli-scale structures. In the case of L. purpureus only one structure -- the distal barbule -- is visible over most of the area. By contrast, in C. cupreus, three milli-scale structures -- the rami, distal barbules, and proximal barbules -- are clearly distinguished in the data; we can observe that reflectance from the feather is oriented with respect to the longitudinal axis of each structure (Figure 8).
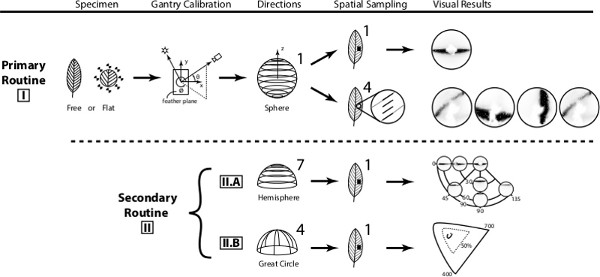
Figure 1. This schematic overview depicts two mounting methods, the spherical gantry coordinate system, types of acquisition sampling and their respective results. Click here to view larger figure.
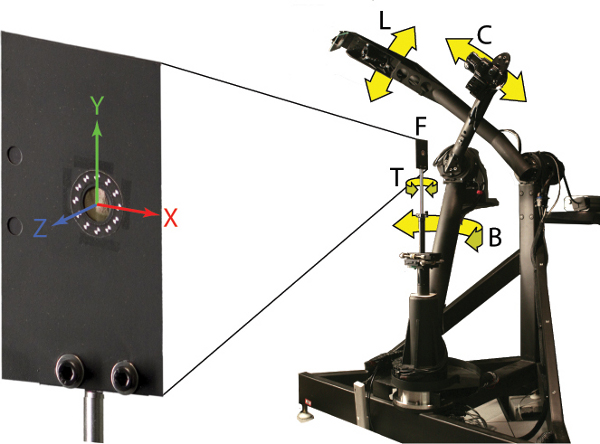
Figure 2. The flattened feather is visible through an aperture in a metal plate surrounded by a ring of targets. A spherical gantry can be posed to measure light scattering from a feather at multiple incident lighting and viewing directions. L=Light arm (latitude). C= Camera arm (latitude). B=Camera Base (longitude). T=Turntable (longitude). F=Feather.
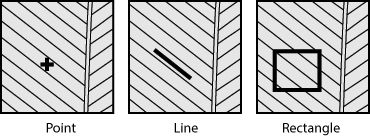
Figure 3. Average directional scattering may be computed from a point, line or rectangular region of feather vane.
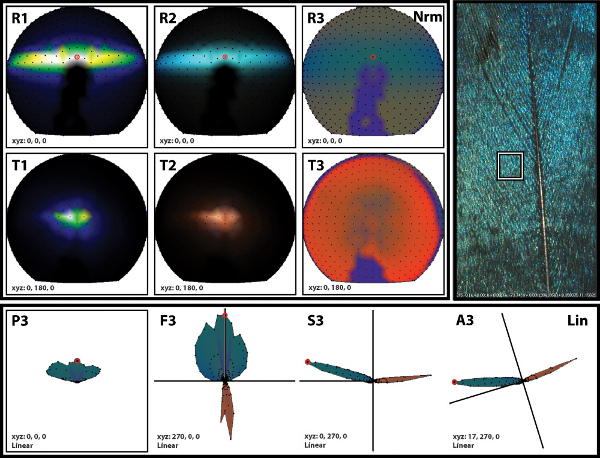
Figure 4. Example of directional scattering plotting functions (R*=Reflectance, T*=Transmittance, P*=Top, F*=Front, S*=Side, A*=Arbitrary) and color schemes (*1=Luminance, *2=RGB, *3=Chromaticity). Click here to view larger figure.
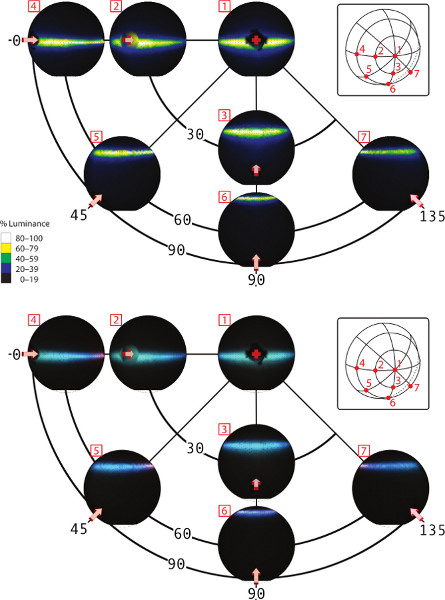
Figure 5. The luminance (top) and RGB color (bottom) of the hemispherical reflectance in direction cosine space as viewed from the (elevation angle, azimuth angle) coordinate pairs: {0°,0°}, {30°,0°}, {30°,90°}, {60°,0°}, {60°,45°}, {60°,90°}, and {60°,135°}. The reflectance is averaged from a 25×25 pixel rectangular region of the lateral vane of a tertial L. purpureus (Purple Glossy Starling) feather. The red arrows represent camera directions. Click here to view larger figure.
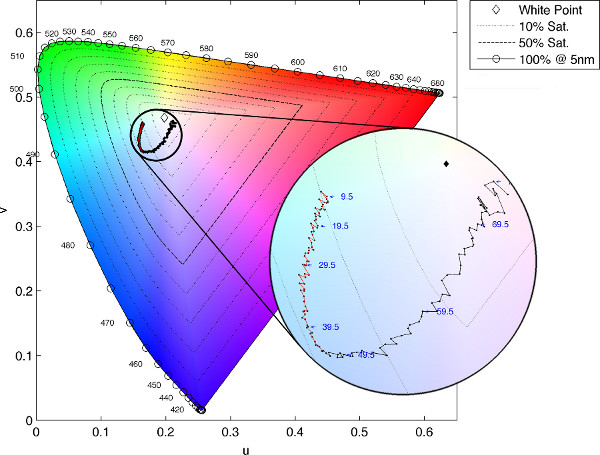
Figure 6. Chromaticity of the reflectance as a function of the half-angle between the incident lighting and viewing directions: CIE 1976 Uniform Chromaticity Scales (USC) with magnified region. Click here to view larger figure.
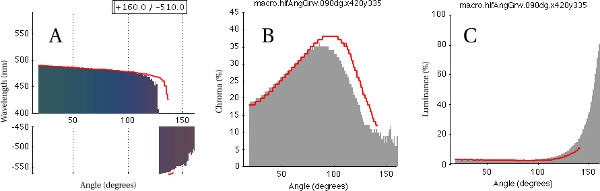
Figure 7. Reflectance as a function of the angle between the incident lighting and viewing directions, in-plane with (red) and perpendicular to (shaded) the longitudinal axis of the distal barbule: (A) Dominant wavelength, (B) Percent chroma, (C) Percent luminance. The color shading in plot A is the RGB color of the reflectance. Negative wavelength values represent colors in the non-spectral purple triangle. Click here to view larger figure.
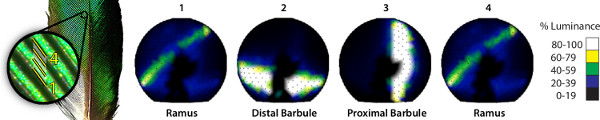
Figure 8. Average directional reflectance of distal barbules and proximal barbules between two adjacent rami of the C. cupreus (African Emerald Cuckoo).

Figure 9. (A) Non-rectified image illuminated by gantry lamp, (B) Non-rectified image illuminated by flash on camera, (C) Filtered target candidates on affine-transformed, flash-illuminated image, (D) Acceptably sharp targets within depth of field, (E) Rectified lamp-illuminated image, (F) Rotated feather tip up, cropped and masked. Click here to view larger figure.
Discussion
Though the performance and function of many pigmentary and structural colorations are well recognized, the morphology of many integuments is so complex that their structural detail and function are poorly understood20. Integuments have developed specializations that vary spatially over the surface of the organism to differentially reflect light directionally toward the viewer. Directionality has received attention primarily in the study of iridescence due to its color shift with change of incident and viewing angle, and research into iridescence of biological integument has garnered primarily 1D and some 2D measurements8,12,17. But generalized 6D measurements have not been routine in the study of integuments21-23, iridescent or otherwise, and the literature on organismal color phenotypes is constrained by the lack of directional color data of the type our method provides.
The feather is an especially rich integumentary material comprising arrangements of milli-scale structure of the barb: rami, distal barbules, and proximal barbules. The small scale of the elements and their complex arrangements make it difficult to discern the light scattering performance of the individual elements. Our protocol successfully isolated milli-scale structure from the influence of macro-scale geometry. By characterizing the functional consequences of the directional expression of milli-scale structures to the far-field signature of the feather, we enabled inquiry into their adaptive consequences.
We faced practical tradeoffs between spectral, spatial and angular resolution. We chose high spatial, medium angular and low spectral for our studies. Other combinations could be used, but some (e.g. all high) lead to unworkably long measurement times. Attention must be focused where it is important for the particular phenomena being studied. In choosing to employ an RGB camera with a Bayer filter mosaic, we designed our protocol to match the human visual system. The RGB camera could be replaced and our protocol adapted to measure the relative color stimulus of any organism, e.g. sensitivity in the UV spectrum is needed to measure avian tetra-chromatic color24,25. A spectral imaging camera would provide the most general solution25.
We demonstrated our protocol with tertial wing feathers since they are colorful and easily flattened against a reference plate. Unfortunately, the aperture of the metal plate revealed only a fraction of the feather surface. If we could simultaneously measure the 3D shape of the feather surface while measuring its reflectance25, we could avoid mechanically flattening the feather and instead measure the entire feather in its natural, unflattened state.
Interactive, specialized, integrated tools for visualizing data provide substantial benefit to scientists exploring and interpreting large data volumes. The greater the integration and interactivity, the easier connections in the data are observed. In our software, a user can interactively plot average directional scattering as a function of surface position (Figure 4). Further development of our software could integrate other plotting functions (Figures 6, 7) to extend the interactive experience.
Disclosures
No conflicts of interest declared.
Acknowledgements
This research was funded by the National Science Foundation (NSF CAREER award CCF-0347303 and NSF grant CCF-0541105). The authors would like to thank Jaroslav Křivánek, Jon Moon, Edgar Velázquez-Armendáriz, Wenzel Jakob, James Harvey, Susan Suarez, Ellis Loew, and John Hermanson for their intellectual contributions. The Cornell Spherical Gantry was built from a design due to Duane Fulk, Marc Levoy, and Szymon Rusinkiewicz.
References
- Nicodemus, F., Richmond, J., Hsia, J., Ginsberg, I., Limperis, T. . Geometric considerations and nomenclature for reflectance. , (1977).
- Marschner, S. R., Jensen, H. W., Cammarano, M., Worley, S., Hanrahan, P. Light scattering from human hair fibers. ACM Transactions on Graphics (TOG). 22 (3), 780-791 (2003).
- Marschner, S. R., Westin, S., Arbree, A., Moon, J. Measuring and modeling the appearance of finished wood. ACM Transactions on Graphics (TOG). 24 (3), 727-734 (2005).
- Land, M. F. The physics and biology of animal reflectors. Progress in Biophysics and Molecular Biology. 24, 75-106 (1972).
- Durrer, H. Colouration. Biology of the Integument: Vertebrates. 2 (12), 239-247 (1986).
- Brink, D., van der Berg, N. Structural colours from the feathers of the bird Bostrychia hagedash. Journal of Physics D-Applied Physics. 37 (5), 813-818 (2004).
- Kinoshita, S. . Structural colors in the realm of nature. , (2008).
- Nakamura, E., Yoshioka, S. Structural Color of Rock Dove's Neck Feather. Journal of the Physical Society of Japan. 77 (12), 124801 (2008).
- Westin, S., Arvo, J., Torrance, K. E. Predicting reflectance functions from complex surfaces. ACM SIGGRAPH Computer Graphics. 26 (2), 255-264 (1992).
- Shawkey, M. D., Maia, R., D'Alba, L. Proximate bases of silver color in anhinga (Anhinga anhinga) feathers. Journal of Morphology. 272 (11), 1399-1407 (2011).
- Maia, R., D'Alba, L., Shawkey, M. D. What makes a feather shine? A nanostructural basis for glossy black colours in feathers. Proceedings of the Royal Society B: Biological Sciences. 278 (1714), 1973-1980 (2011).
- Dyck, J. Structure and light reflection of green feathers of fruit doves (Ptilinopus spp.) and an Imperial Pigeon (Ducula concinna). Biologiske Skrifter (Denmark). 30, 2-43 (1987).
- Yoshioka, S., Kinoshita, S. Effect of macroscopic structure in iridescent color of the peacock feathers. Forma. 17 (2), 169-181 (2002).
- Osorio, D., Ham, A. Spectral reflectance and directional properties of structural coloration in bird plumage. Journal of Experimental Biology. 205 (14), 2017-2027 (2002).
- Stavenga, D. G., Leertouwer, H. L., Pirih, P., Wehling, M. F. Imaging scatterometry of butterfly wing scales. Optics Express. 1 (1), 193-202 (2009).
- Vukusic, P., Stavenga, D. G. Physical methods for investigating structural colours in biological systems. Journal of Royal Society Interface. 6, S133-S148 (2009).
- Stavenga, D. G., Leertouwer, H., Marshall, N. J., Osorio, D. Dramatic colour changes in a bird of paradise caused by uniquely structured breast feather barbules. Proceedings of the Royal Society B: Biological Sciences. 278 (1715), 2098-2104 (2010).
- Irawan, P. . Appearance of woven cloth [dissertation]. , (2008).
- Irawan, P., Marschner, S. R. Specular reflection from woven cloth. ACM Transactions on Graphics (TOG. 31 (1), 11:1-11:20 (2012).
- Vukusic, P. Structural colour: elusive iridescence strategies brought to light. Current Biology: CB. 21 (5), R187-R189 (2011).
- Dana, K., Ginneken, B., Nayar, S., Koenderink, J. Reflectance and texture of real-world surfaces. ACM Transactions on Graphics (TOG). 18 (1), 1-34 (1999).
- Chen, Y., Xu, Y., Guo, B., Shum, H. -. Y. Modeling and rendering of realistic feathers. ACM Transactions on Graphics (TOG). 21 (3), 630-636 (2002).
- Levoy, M., Zhang, Z., McDowall, I. Recording and controlling the 4D light field in a microscope using microlens arrays. Journal of microscopy. 235 (2), 144-162 (2009).
- Stevens, M., Párraga, C. A., Cuthill, I. C., Partridge, J. C., Troscianko, T. S. Using digital photography to study animal coloration. Biological Journal of the Linnean Society. 90 (2), 211-237 (2007).
- Kim, M. H., Harvey, T. A., et al. 3D imaging spectroscopy for measuring hyperspectral patterns on solid objects. ACM Transactions on Graphics (TOG). 31 (4), (2012).
Reprints and Permissions
Request permission to reuse the text or figures of this JoVE article
Request PermissionThis article has been published
Video Coming Soon
Copyright © 2025 MyJoVE Corporation. All rights reserved