JoVE Logo
Authors
Contact Us

Sign In

A subscription to JoVE is required to view this content. Sign in or start your free trial.

In This Article

  • Summary
  • Abstract
  • Introduction
  • Protocol
  • Results
  • Discussion
  • Disclosures
  • Acknowledgements
  • Materials
  • References
  • Reprints and Permissions

Summary

This paper demonstrates the experimental procedure to measure terminal settling velocities of spherical particles in surfactant-based shear thinning viscoelastic fluids. Fluids over a wide range of rheological properties are prepared and settling velocities are measured for a range of particle sizes in unbounded fluids and fluids between parallel walls.

Abstract

An experimental study is performed to measure the terminal settling velocities of spherical particles in surfactant based shear thinning viscoelastic (VES) fluids. The measurements are made for particles settling in unbounded fluids and fluids between parallel walls. VES fluids over a wide range of rheological properties are prepared and rheologically characterized. The rheological characterization involves steady shear-viscosity and dynamic oscillatory-shear measurements to quantify the viscous and elastic properties respectively. The settling velocities under unbounded conditions are measured in beakers having diameters at least 25x the diameter of particles. For measuring settling velocities between parallel walls, two experimental cells with different wall spacing are constructed. Spherical particles of varying sizes are gently dropped in the fluids and allowed to settle. The process is recorded with a high resolution video camera and the trajectory of the particle is recorded using image analysis software. Terminal settling velocities are calculated from the data.

The impact of elasticity on settling velocity in unbounded fluids is quantified by comparing the experimental settling velocity to the settling velocity calculated by the inelastic drag predictions of Renaud et al.1 Results show that elasticity of fluids can increase or decrease the settling velocity. The magnitude of reduction/increase is a function of the rheological properties of the fluids and properties of particles. Confining walls are observed to cause a retardation effect on settling and the retardation is measured in terms of wall factors.

Introduction

Suspensions of particles in liquids are encountered in applications including pharmaceutical manufacturing, wastewater treatment, space propellant reinjection, semiconductor processing, and liquid detergent manufacturing. In the oil industry, viscoelastic fracturing fluids are used to transport proppants (typically sand) in hydraulic fractures. Upon the cessation of pumping the proppants keep the fracture open and provide a conductive pathway for hydrocarbons to flow back.

Settling of particles is governed by the rheology and density of fluid, size, shape and density of particles and effect of confining walls. For a spherical particle settling in a Newtonian fluid in the creeping flow regime, the settling velocity is given by Stokes equation, derived by Stokes in 1851. Expressions to calculate the drag force at higher Reynolds numbers have been presented by subsequent researchers2-6. Confining walls reduce the settling velocities by exerting a retardation effect on particles. Wall factor, Fw, is defined as the ratio of terminal settling velocity in presence of confining walls to the settling velocity under unbounded conditions. The wall factor quantifies the retardation effect of the confining walls. Many theoretical and experimental studies to determine wall factors for spheres settling in Newtonian fluids in different cross-section tubes over a wide range of Reynolds numbers are available in the literature7-13. In all, there is an extensive body of information available to determine the drag on spheres in Newtonian fluids.

The past work on determination of settling velocity of particles in nonNewtonian fluids, particularly viscoelastic fluids, is less complete. Various numerical predictions14-18 and experimental studies19-24 are available in literature to determine the drag force on a sphere in inelastic power-law fluids. Using the theoretical predictions of Tripathi et al.15 and Tripathi and Chhabra17, Renaud et al.1 developed the following expressions to calculate the drag coefficient (CD) in inelastic power-law fluids.

For RePL<0.1 (creeping flow regime)

figure-introduction-2427
where X(n) is the drag correction factor13. RePL is the Reynolds number for a sphere falling in a power law liquid defined as:

figure-introduction-2796
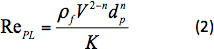
where ρf is the density of the liquid. The drag correction factor was fitted with the following equation1:

figure-introduction-3132
Using the definition of drag coefficient, the settling velocity is calculated as:

figure-introduction-3407
For 0.1<RePL<100

figure-introduction-3662
where X is the ratio of the surface area to the projected area of the particle and is equal to 4 for spheres. CD0 is the drag coefficient in the Stokes region (RePL < 0.1) given by Equation 1, CD∞ is the value of drag coefficient in the Newton's region (RePL > 5 x 102) and is equal to 0.44. The parameters β, b, k are expressed as:

figure-introduction-4342
αo = 3 and α is the correction for the average shear rate related to X(n) as:

figure-introduction-4668
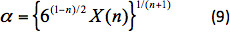
To calculate the settling velocity the dimensionless group Nd 25 is used:

figure-introduction-4966
Nd is independent of the settling velocity and can be calculated explicitly. Using this value and the drag coefficient expression in Equation 5, RePL can be solved iteratively. The settling velocity can be then calculated using:

figure-introduction-5448
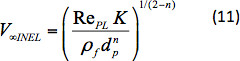
The expressions in Equations 1-9 were based on theoretical predictions obtained for values 1 ≥ n ≥ 0.4. Chhabra13 compared the predictions from the above expressions with experimental results of Shah26-27 (n varied from 0.281-0.762) and Ford et al.28 (n varied from 0.06-0.29). The expressions were shown to predict the drag coefficients accurately. Based on these analyses, the above formulation can be used to calculate the settling velocity of spherical particles in inelastic power-law fluids for 1 ≥ n ≥ 0.06. This predicted settling velocity in inelastic power-law fluids is compared with the experimental velocity in the power-law viscoelastic fluids to determine the influence of fluid elasticity on settling velocity. The detailed steps are mentioned in the next section.

The determination of settling velocity of particles in viscoelastic fluids has also been a topic of research with varying observations by different researchers; (i) In the creeping flow regime the shear thinning effects completely overshadow viscoelastic effects and the settling velocities are in excellent agreement with purely viscous theories29-32, (ii) particles experience a drag reduction in and outside the creeping flow regime and the settling velocities increase due to elasticity30,33,34, (iii) settling velocity reduces due to fluid elasticity35. Walters and Tanner36 summarized that for Boger fluids (constant viscosity elastic fluids) elasticity causes a drag reduction at low Weissenberg numbers followed by drag enhancement at higher Weissenberg numbers. McKinley37 highlighted that the extensional effects in the wake of the sphere cause the drag increase at higher Weissenberg numbers. After a comprehensive review of prior work on settling of particles in unbounded and confined viscoelastic fluids, Chhabra13 highlighted the challenge of incorporating a realistic description of shear rate dependent viscosity together with fluid elasticity in theoretical developments. The study of wall effects on settling of spherical particles has also been an area of research over the past years38-42. However, all the work has been performed on settling of spherical particles in cylindrical tubes. No data is available for spherical particles settling in viscoelastic fluids between parallel walls.

This work attempts to experimental study the settling of spheres in shear thinning viscoelastic fluids. The goal of this experimental study is to understand the impact of fluid elasticity, shear thinning and confining walls on settling velocity of spherical particles in shear thinning viscoelastic fluids. This paper focuses on the experimental methods used for this study along with some representative results. The detailed results along with the analyses can be found in an earlier publication43.

Access restricted. Please log in or start a trial to view this content.

Protocol

1. Preparation of the Fluids

A polymer-free, viscoelastic, two-component, surfactant-based fluid system is used for this experimental study. This fluid system has been used in oil and gas wells in many producing fields for hydraulic fracturing treatments44,45. This fluid system is used for this study because it is optically transparent and the rheology can be controlled by systematically varying the concentrations and proportions of the two components. The fluid system consists of a an anionic surfactant (such as sodium xylene sulfonate) as component A and a cationic surfactant (such as N,N,N-trimethyl-1-octadecamonium chloride) as component B.

  1. Add a given concentration of component A to distilled water and mix at high rpm using an overhead mixer to ensure proper mixing. Allow it to mix for 2-3 min.
  2. Add a given concentration of component B to this mixture and allow it to mix for an additional 2-3 min.
  3. Rest the mixture for 2-6 hr to vent out the air bubbles. Note: The final fluid mixture is optically transparent. For this study seven fluid mixtures of different concentrations are used. The concentrations are chosen to obtain fluid mixture over a wide range of viscosities.

2. Measurement of Settling Velocities in Unbounded Fluids

Glass spheres of diameters ranging from 1-5 mm are used.

  1. Use a high resolution microscope to measure the diameter of the glass spheres. Ensure that the spheres have smooth surfaces and are near-perfect spheres.
  2. Store the liquid in glass containers with diameter at least 25x the diameter of particles to ensure that there is no effect of the confining walls on the settling velocity of particles.
  3. Record the room temperature and fluid temperature using a laboratory thermometer. The measurement of temperature is important because the rheological measurements of the fluid should be made at the temperature at which the settling experiment is performed.
  4. Place a meter stick alongside the container.
  5. Gently immerse the glass particle in the liquid and allow it to settle. Record the settling process with a high resolution video camera.
  6. Track the position of the particle at different time steps from the recorded video using an image analysis application. Note: In this work, a software application called 'Tracker' is used (http://www.cabrillo.edu/~dbrown/tracker/).
  7. Plot the vertical position of the particle versus time and calculate the terminal settling velocity from the slope of the line.
  8. Repeat the experiment under the unique set of conditions at least 3x to ensure reproducibility. Perform the image analysis for different measurements and report the settling velocity for a given particle diameter in a particular fluid using error bars.
  9. Repeat the above steps for different diameter particles and record the settling velocities. Plot the settling velocity versus particle diameter. Note: Figure 1 shows the settling velocity of five different size particles in one fluid.

3. Measurement of Settling Velocities for Fluids Between Parallel Walls

To measure the settling velocities in presence of parallel walls, two experimental cells made of Plexiglas are used.

  1. While designing and constructing the cell, ensure that the walls are smooth and perfectly parallel to each other. Keep the aspect ratio of the cells low to ensure that there is no effect of the walls orthogonal to the parallel walls. Note: The gap between the walls in the two cells in this study is 3.6 mm and 8 mm, respectively. Figure 2 shows a schematic of one experimental cell.
  2. Fill the cell with the liquid and gently release the particle in the cell through the inlet/outlet port. Seal the inlet/outlet port with a rubber stopper and allow the particle to settle until it reaches the middle of the cell.
  3. At this point, carefully position the cell vertically and allow the particle to settle.
  4. Place a meter stick alongside the cell and record the settling using the high resolution video camera.
  5. Record the room temperature and fluid temperature using a laboratory thermometer. This is important because the rheological measurements of the fluid should be made at this temperature.
  6. As with the unbounded settling velocity measurements, measure the settling velocity in software application 'Tracker'. Repeat the measurements at least three times to ensure reproducibility and to obtain error bars on each measurement.

4. Rheological Characterization of Fluids

  1. Perform the steady shear-viscosity measurements to measure the viscosity of the fluid as a function of shear rate. Note: In this work, the ARES rheometer by TA Instruments with a double wall concentric cylinder fixture (inside cup diameter: 27.95 mm, inside bob diameter: 29.50 mm, outside bob diameter: 32.00 mm, outside cup diameter: 34.00 mm, bob length: 32.00 mm) is used.
  2. Vary the shear rate from 0.1-800 sec-1 and take measurements at 10 points/decade. Ensure that the temperature of the cup is the same at which the settling experiment was performed in the same fluid. Figure 3 shows viscosity versus shear rate for one fluid sample on a log-log plot.
  3. For the same fluid, calculate the range of shear rate which the particles encountered in the settling experiments. Use the surface averaged particle shear rate defined by 2V/dp 20,23, where V is the settling velocity of the particle and dp is the particle diameter.
  4. Fit a power-law curve μ=Kγn-1in this range of shear rates on the viscosity versus shear rate plot. On a log-log plot this fit will be a straight line. Determine the parameters K (flow consistency index) and n (flow behavior index).
    K and n quantify the viscosity of the fluids. Figure 3 shows the power-law fit on the same plot.
  5. Perform the dynamic oscillatory-shear measurements over the range of frequencies from 0.1-100 rad/sec and measure the elastic modulus, G' and viscous modulus, G''. Take measurement at 10 points/decade.
    Figure 4 shows the G' and G'' for a fluid sample.
  6. Calculate the ratio of the two moduli, G''/G' from this data. Fit the ratio of moduli to a Maxwell model using a regression analysis and calculate the relaxation time (λ) of the fluid. The equation for the ratio of the two moduli for a Maxwell model is46,47:

figure-protocol-7179
The relaxation time of the fluid quantifies the elasticity of the fluid. Greater the relaxation time, more elastic is the fluid. Figure 5 shows the G''/G' for the fluid sample along with the Maxwell fit. The fitting is performed by minimizing the sum of the variance measure over the frequency range.
figure-protocol-7663

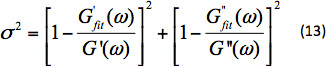
5. Determining the Influence of Elasticity on Unbounded Settling Velocities

  1. Denote the experimental settling velocity of a particle in unbounded fluid by V∞VE where '∞VE' refers to unconfined viscoelastic fluids. Compare this experimental settling velocity with the settling velocity (V∞INEL) calculated on the basis of apparent viscosity data based on the power-law parameters. Use the expressions developed by Renaud et al.1 to calculate V∞INEL. The expressions are mentioned in the Introduction section. '∞INEL' refers to unconfined inelastic fluids.
  2. Calculate the ratio V∞EL/V∞INEL , and refer to the ratio as the velocity ratio.
    The value of the velocity ratio illustrates the influence of elasticity on settling velocity. Velocity ratio greater than 1 suggests velocity increase/ drag reduction due to fluid elasticity. Velocity ratio less than 1 suggests velocity reduction/drag enhancement due to fluid elasticity.
  3. Plot the velocity ratio as a function of particle diameter for different fluids to observe the effect of elasticity on settling velocity of different diameter particles in fluids of different rheologies. Figure 6 shows the velocity ratio as a function of particle diameter in one of the fluids.

6. Quantifying the Retardation Effect of Parallel Walls on Settling Velocities

  1. Calculate the wall factor, Fw for a given diameter particle by dividing the settling velocity in the presence of parallel walls, V∞VE to the settling velocity in the unbounded fluid, V∞VE.
  2. For a given fluid, plot the wall factors as a function of the particle diameter to wall spacing ratio, r. Figure 7 shows the wall factors for particles settling in one of the fluids. The plot helps quantify the retardation effect of the confining walls on settling velocity. Lower the wall factor, higher the wall retardation effect.

Access restricted. Please log in or start a trial to view this content.

Results

The experiments are performed for five different diameter particles in seven different fluid mixtures with unique K, n and λ values. Figure 1 shows the settling velocity as a function of particle diameter in one fluid. The error bars shows the variability in the three measurements. The room temperature measured during the experiment is 23 °C. It can be observed that the settling vel...

Access restricted. Please log in or start a trial to view this content.

Discussion

The experimental study focuses on measurement of settling velocities of spherical particles in shear thinning viscoelastic fluids under unconfined and confined conditions. Detailed experimental procedure to obtain repeatable measurements of settling velocities is presented. Results are presented to show that fluid elasticity can increase or decrease the settling velocity. Walls exert a retardation effect on settling and this effect is measured in terms of wall factors.

Prior to the experiments...

Access restricted. Please log in or start a trial to view this content.

Disclosures

The authors would like to point out that the goal of this publication is visual demonstration of experimental procedure for measuring settling of particles. For detailed results and analyses the readers should refer to the earlier publication43.

Acknowledgements

The authors are grateful to DOE and RPSEA for the financial support and to the companies sponsoring the JIP on Hydraulic Fracturing and Sand Control at the University of Texas at Austin (Air Liquide, Air Products, Anadarko, Apache, Baker Hughes, BHP Billiton, BP America, Chevron, ConocoPhillips, ExxonMobil, Ferus, Halliburton, Hess, Linde Group, Pemex, Pioneer Natural Resources, Praxair, Saudi Aramco, Schlumberger, Shell, Southwestern Energy, Statoil, Weatherford, and YPF).

Access restricted. Please log in or start a trial to view this content.

Materials

NameCompanyCatalog NumberComments
Glass MicrospheresWhitehouse Scientific#GP1750Available in different sieve fractions.
RheometerTA InstrumentsARESAny standard rheometer capable of taking dynamic and static measurements
Anionic Surfactant (Component A)Proprietary fluidUsed in oil field services for hydraulic fracturing. Sodium Xylene Sulfonate can be used as a substitute.
Cationic Surfactant (Component B)Proprietary fluidUsed in oil field services for hydraulic fractuing. N,N,N-Trimethyl-1-Octadecamonium Chloride can be used as a substitute.

References

  1. Renaud, M., Mauret, E., Chhabra, R. P. Power-law fluid flow over a sphere: average shear rate and drag. 82, 1066-1070 (2004).
  2. Clift, R., Grace, J. R., Weber, M. E. Bubbles, Drops and Particles. , Academic Press. New York. (1978).
  3. Khan, A. R., Richardson, J. F. The resistance to motion of a solid sphere in a fluid. Chem. Eng. Sci. 62, 135-150 (1987).
  4. Zapryanov, Z., Tabakova, S. Dynamics of Bubbles, Drops and Rigid Particles. , Kluwer Academic Publishers. Dordrecht, The Netherlands. (1999).
  5. Michaelides, E. E. Chapter 2. Analytical expressions for the motion of particles. Transport Processes in Bubbles Drops and Particles. DeKee, D., Chhabra, R. P. , 2nd edition, Taylor & Francis. New York. (2002).
  6. Michaelides, E. E. Hydrodynamic force and heat/mass transfer from particles, bubbles and drops - the Freeman Scholar Lecture. Journal of Fluids Engineering (AMSE. 125, 209-238 (2003).
  7. Der Faxen, H. Widerstand gegen die Bewegung einer starren Kugel in einer zähen Flüssigkeit, die zwischen zwei parallelen ebenen Wänden eingeschlossen ist). Annalen der Physics. 68, 89-119 (1922).
  8. Bohlin, T. On the drag on a sphere moving in a viscous fluid inside a cylindrical tube. Trans Royal Insitute of Technology Stockholm. 155, (1960).
  9. Miyamura, A., Iwasaki, S., Ishii, T. Experimental wall correction factors of single solid spheres in triangular and square cylinders, and parallel plates. International Journal of Multiphase Flow. 7, 41-46 (1981).
  10. Tullock, D. L., Phan-Thien, N., Graham, A. L. Boundary element simulations of spheres settling in circular, square and triangular ducts. Rheol. Acta. 31, 139-150 (1992).
  11. Chhabra, R. P. Wall effects on terminal velocity of non-spherical particles in non-Newtonian polymer solutions. Powder Technology. 88, 39-44 (1996).
  12. Chhabra, R. P. Chapter 2. Wall effects on spheres falling axially in cylindrical tubes. Transport Processes in Bubbles Drops and Particles. Dekes, D., Chhabra, R. P. , 2nd edition, Taylor & Francis. New York. (2002).
  13. Chhabra, R. P. Bubbles, Drops, and Particles in Non-Newtonian Fluids. Francis, S. econded.,T. aylor& , Florida. (2007).
  14. Dazhi, G., Tanner, R. I. The drag on a sphere in a power law fluid. Journal of Non-Newtonian Fluid Mechanics. 17, 1-12 (1984).
  15. Tripathi, A., Chhabra, R. P., Sundararajan, T. Power-law fluid over spheroidal particles. Industrial & Engineering Chemistry Research. 33, 403-410 (1994).
  16. Graham, D. I., Jones, T. E. R. Settling and transport of spherical particles in power-law fluids at finite Reynolds number. Journal of Non-Newtonian Fluid Mechanics. 54, 465-488 (1994).
  17. Tripathi, A., Chhabra, R. P. Drag on spheroidal particles in dilatant fluids. AIChE. 41 (3), 728-731 (1995).
  18. Missirlis, K. A., Assimacopoulos, D., Mitsoulis, E., Chhabra, R. P. Wall effects for motion of spheres in power-law fluids. Journal of Non-Newtonian Fluid Mechanics. 96 (3), 459-471 (2001).
  19. Dallon, D. S. A drag coefficient correlation for spheres settling in Ellis fluids [Ph.D. Dissertation]. , University of Utah. Salt Lake City, Utah. (1967).
  20. Uhlherr, P. H. T., Le, T. N., Tiu, C. Characterization of inelastic power-law fluids using falling sphere data. Canadian Journal of Chemical Engineering. 54, 497-502 (1976).
  21. Machac, I., Lecjaks, Z. Wall Effect for a Sphere Falling Through a Non-Newtonian Fluid in a Rectangular Duct. Chemical Engineering Science. 50 (1), 143-148 (1995).
  22. Kelessidis, V. C., Mpandelis, G. Measurements and prediction of terminal velocity of solid particles falling through stagnant pseudoplastic liquids. Powder Technology. 147, 117-125 (2004).
  23. Shah, S. N., Fadili, Y. E., Chhabra, R. P. New model for single spherical particle settling velocity in power law (visco-inelastic) fluids. International Journal of Multiphase Flow. 33, 51-66 (2007).
  24. Rodrigue, D., DeKee, D., Chan Man Fong, C. F. The slow motion of a spherical particle in a Carreau fluid. Chemical Engineering Communications. 154, 203-215 (1996).
  25. Darby, R. Chemical Engineering Fluid Mechanics. , 2nd edition, Marcel dekker. New York. (2001).
  26. Shah, S. N. Proppant settling correlations for non-Newtonian fluids. Society of Petroleum Engineers Journal. 22 (2), 164-170 (1982).
  27. Shah, S. N. Proppant-settling correlations for non-Newtonian Fluids. Society of Petroleum Engineers Production Engineering Journal. 1 (6), 446-448 (1986).
  28. The formulation of milling fluids for efficient hole cleaning: an experimental investigation. Paper SPE 38819. Ford, J. T., Oyeneyin, M. B., et al. European Petroleum Conference, 1994 Oct 25-27, London, U.K, , (1994).
  29. Acharya, A., Mashelkar, R. A., Ulbrecht, J. Flow of inelastic and viscoelastic fluids past a sphere, Part II: Anomalous separation in the viscoelastic fluid flow. Rheological Acta. 15, 471-478 (1976).
  30. Acharya, A. R. Viscoelasticity of crosslinked fracturing fluids and proppant transport. SPE Production Engineering. 3, 483-488 (1988).
  31. Chhabra, R. P., Uhlherr, P. H. T. Creeping motion of spheres through shear-thinning elastic fluids described by the Carreau viscosity equation. Rheological Acta. 19 (2), 187-195 (1980).
  32. Bush, M. B., Phan-Thien, N. Drag force on a sphere in creeping motion through a Carreau model fluid. Journal of Non-Newtonian Fluid Mechanics. 16 (3), 303-313 (1984).
  33. Broadbent, J. M., Mena, B. Slow flow of an elastico-viscous fluid past cylinders and spheres. Chemical Engineering Journal. 8, 11-19 (1974).
  34. Sigli, D., Coutanceau, M. Effect of finite boundaries on the slow laminar isothermal flow of a viscoelastic fluid around a spherical obstacle. Journal of Non-Newtonian Fluid Mechanics. 2, 1-21 (1977).
  35. Brule, B. H. A. A. V. D., Gheissary, G. Effects of fluid elasticity on the static and dynamic settling of a spherical particle. Journal of Non-Newtonian Fluid Mechanics. 49, 123-132 (1993).
  36. Walters, K., Tanner, R. I. Chapter 3. The Motion of a Sphere through an Elastic Fluid.. Transport Processes in Bubbles, Drops and Particles. Chhabra, R. P. D. eK. ee,D. .,, DeKee, D. , Hemisphere. New York. (1992).
  37. McKinley, G. H. Chapter 14. Steady and transient motion of spherical particles in viscoelastic liquids. Transport Processes in Bubbles, Drops and Particles. DeKee, D., Chhabra, R. P. , 2nd edition, Taylor & Francis. New York. (2002).
  38. Chhabra, R. P., Tiu, C., Uhlherr, P. H. T. A study of wall effects on the motion of a sphere in viscoelastic fluids. Canadian Journal of Chemical Engineering. 59, 771-775 (1981).
  39. Jones, W. M., Price, A. H., Walters, K. The motion of a sphere falling under gravity in a constant viscosity elastic liquid. Journal of Non-Newtonian Fluid Mechanics. 53, 175-196 (1994).
  40. Navez, V., Walters, K. A note on settling in shear-thinning polymer solutions. Journal of Non-Newtonian Fluid Mechanics. 67, 325-334 (1996).
  41. Huang, P. Y., Wall Feng, J. effects on the flow of viscoelastic fluids around a circular cylinder. Journal of Non-Newtonian Fluid Mechanics. 60, 179-198 (1995).
  42. Sugeng, F., Tanner, R. I. The drag on spheres in viscoelastic fluids with significant wall effects. Journal of Non-Newtonian Fluid Mechanics. 20, 281-292 (1986).
  43. Malhotra, S., Sharma, M. M. Settling of Spherical Particles in Unbounded and Confined Surfactant-Based Shear Thinning Viscoelastic Fluids: An Experimental Study. Chemical Engineering Science. 84, 646-655 (2012).
  44. Zhang, K. Fluids for Fracturing Subterranean Formations.U.S. US patent. , 6,468,945 (2002).
  45. Gupta, D. V. S., Leshchyshyn, T. T., Hlidek, B. T. Surfactant gel foam/emulsions: History and field application in the western Canadian sedimentary basin. SPE Annual Technology Conference and Exhibition, 2005 Oct 9-12, Dallas, , Dallas. (2005).
  46. Ferry, J. D. Viscoelastic Properties of Polymers. , 2nd edition, John Wiley & Sons, Inc.. USA. (1970).
  47. Yesilata, B., Clasen, C., McKinley, G. H. Nonlinear shear and extensional Flow dynamics of wormlike surfactant solutions. Journal of Non-Newtonian Fluid Mechanics. 133, 73-90 (2006).

Access restricted. Please log in or start a trial to view this content.

Reprints and Permissions

Request permission to reuse the text or figures of this JoVE article

Request Permission

Explore More Articles

Keywords Experimental MeasurementSettling VelocitySpherical ParticlesUnconfinedConfinedSurfactant basedShear ThinningViscoelastic FluidsRheological PropertiesSteady Shear viscosityDynamic Oscillatory shearUnbounded ConditionsParallel WallsTerminal Settling VelocitiesDrag PredictionsElasticityWall Factors

This article has been published

Video Coming Soon

JoVE Logo

Privacy

Terms of Use

Policies

Contact Us

Recommend to library

JoVE NEWSLETTERS

Research

Education

Authors

Librarians

ABOUT JoVE

Copyright © 2025 MyJoVE Corporation. All rights reserved