Authors
Contact Us

Sign In

A subscription to JoVE is required to view this content. Sign in or start your free trial.

In This Article

  • Summary
  • Abstract
  • Introduction
  • Protocol
  • Results
  • Discussion
  • Disclosures
  • Acknowledgements
  • Materials
  • References
  • Reprints and Permissions

Summary

The main goal of this work is to make it easier for research groups unfamiliar with Langmuir probes and emissive probes to use them as plasma diagnostics, especially near plasma boundaries. We do this by demonstrating how to build the probes from readily available materials and supplies.

Abstract

Langmuir probes have long been used in experimental plasma physics research as the primary diagnostic for particle fluxes (i.e., electron and ion fluxes) and their local spatial concentrations, for electron temperatures, and for electrostatic plasma potential measurements, since its invention by Langmuir in the early 1920s. Emissive probes are used for measuring plasma potentials. The protocols exhibited in this work serve to demonstrate how these probes may be built for use in a vacuum chamber in which a plasma discharge may be confined and sustained. This involves vacuum techniques for building what is essentially an electrical feedthrough, one that is rotatable and translatable. Certainly, complete Langmuir probe systems may be purchased, but they can also be built by the user at considerable cost savings, and at the same time be more directly adapted to their use in a particular experiment. We describe the use of Langmuir probes and emissive probes in mapping the electrostatic plasma potential from the body of the plasma up to the sheath region of a plasma boundary, which in these experiments is created by a negatively biased electrode immersed within the plasma, in order to compare the two diagnostic techniques and assess their relative advantages and weaknesses. Although Langmuir probes have the advantage of measuring the plasma density and electron temperature most accurately, emissive probes can measure electrostatic plasma potentials more accurately throughout the plasma, up to and including the sheath region.

Introduction

During this first century of plasma physics research, dating from Langmuir’s discoveries in the 1920s of the medium like behavior of a new state of matter, plasma, the Langmuir probe has proved to have been the single most important diagnostic of plasma parameters. This is true in part, because of its extraordinary range of applicability1. In plasma encountered by satellites2,3,4, in semiconductor processing experiments,5,6,7,8 at the edges of plasma confined in tokamaks,9,10,11 and in wide range of basic plasma physics experiments, Langmuir probes have been used to measure plasma densities and temperatures spanning the ranges 108≤ne≤1019m-3, and 10-3≤Te≤102eV , respectively. Simultaneously in the 1920s, he invented the probe now named after him and the emissive probe12. The emissive probe is now primarily used as a diagnostic of plasma potential. Although it cannot measure the breadth of plasma parameters that the Langmuir probe can, it too is a diagnostic of wide utility when it comes to the measurement of plasma potential, or, as it is sometimes called, the electrostatic space potential. For example, the emissive probe can accurately measure space potentials even in a vacuum, where Langmuir probes are incapable of measuring anything.

The basic setup of the Langmuir probe consists of putting an electrode into the plasma and measuring the collected current. The resulting current-voltage (I-V) characteristics can be used to interpret plasma parameters such as electron temperature Te, electron density ne, and plasma potential ϕ13. For a Maxwellian plasma, the relationship between collected electron current Ie (taken to be positive) and probe bias VB can be expressed as14:

figure-introduction-2430

where Ie0 is the electron saturation current,

figure-introduction-2614

and where S is the collecting area of the probe, 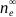figure-introduction-2762 is the bulk electron density, e is the electron charge, Te is the electron temperature, me is the electron mass. The theoretical relation of I-V characteristics for the electron current is illustrated in two ways in Figure 1A and Figure 1B. Note, Eq. (1a,b) only applies to bulk electrons. However, Langmuir probe currents can detect flows of charged particles, and adjustments must be made in the presence of primary electrons, electron beams, or ion beams etc. See Hershkowitz14 for more details.

The discussion here takes up the ideal case of Maxwellian electron energy distribution functions (EEDF). Of course, there are many circumstances in which non-idealities arise, but these are not the subject of this work. For example, in materials processing etching and deposition plasma systems, typically RF generated and sustained, there are molecular gas feed stocks that produce volatile chemical radicals in the plasma, and multiple ion species including negatively charged ions. The plasma becomes electronegative, that is, having a significant fraction of the negative charge in the quasineutral plasma in the form of negative ions. In plasma with molecular neutrals and ions, inelastic collisions between electrons and the molecular species can produce dips15 in the current-voltage characteristics, and the presence of cold negative ions, cold relative to the electrons, can produce significant distortions16 in the vicinity of the plasma potential, all of which of course are non-Maxwellian features. We prosecuted the experiments in the work discussed in this paper in a single ion species noble gas (argon) DC discharge plasma, free of these kinds of non-Maxwellian effects. However, a bi-Maxwellian EEDF is typically found in these discharges, caused by the presence of secondary electron emission17 from the chamber walls. This component of hotter electrons is typically a few multiples of the cold electron temperature, and less than 1% of the density, typically easily distinguished from the bulk electron density and temperature.

As VB becomes more negative than ϕ, electrons are partially repelled by the negative potential of the probe surface, and the slope of the ln(Ie) vs. VB is e/Te, ie. 1/TeV where TeV is the electron temperature in eV, as shown in Figure 1B. After TeV is determined, the plasma density can be derived as:

figure-introduction-5586

Ion current is derived differently than electron current. Ions are assumed to be “cold” due to their relatively large mass, Mi >> me, compared to that of the electron, thus, in a weakly ionized plasma, the ions are in fairly good thermal equilibrium with the neutral gas atoms, which are at the wall temperature. Ions are repelled by the probe sheath if VB ≥ ϕ and collected if VB < ϕ. The collected ion current is approximately constant for negatively biased probes, while the electron flux to the probe decreases for probe bias voltages more negative than the plasma potential. Since the electron saturation current is much larger than the ion saturation current, the total current collected by the probe decreases. As the probe bias becomes increasingly negative, the drop in current collected is great or small as the electron temperature is cold or hot, as described above in Eq. (1a). The equation for ion current in this approximation is:

figure-introduction-6784

where

figure-introduction-6917

and

figure-introduction-7048

We note that constant ion flux collected by the probe exceeds the random thermal ion flux due to acceleration along the presheath of the probe and thus ions reach the sheath edge of the probe at the Bohm speed18, uB, rather than the ion thermal speed19. And the ions have a density equal to the electrons since the presheath is quasineutral. Comparing the ion and electron saturation current in Eqn.5 and 2, we observe that the ion contribution to the probe current is smaller than that of electrons by a factor of figure-introduction-7721. This factor is about 108 in the case of argon plasma.

There is a sharp transition point where the electron current goes from exponential to a constant, known as the ”knee”. The probe bias at the knee can be approximated as the plasma potential. In the real experiment, this knee is never sharp, but rounded due to the space-charge effect of the probe, that is, the expansion of the sheath surrounding the probe, and also to probe contamination, and plasma noise13.

The Langmuir probe technique is based on collection current, whereas the emissive probe technique is based on the emission of current. Emissive probes measure neither temperature nor density. Instead they provide precise plasma potential measurements and can operate under a variety of situations due to the fact that they are insensitive to plasma flows. The theories and usage of emissive probes are fully discussed in the topical review by Sheehan and Hershkowitz20, and references therein.

For plasma density 1011 ≤ ne ≤ 1018 m-3, the inflection point technique in the limit of zero emission is recommended, which means to take a of series of I-V traces, each with different filament heating currents, finding the inflection point bias voltage for each I-V trace, and extrapolate the inflection points to the limit of zero emission to get the plasma potential, as shown in Figure 2.

It is a common assumption that Langmuir and emissive probe techniques agree in quasineutral plasma, but disagree in the sheath, the region of the plasma in contact with the boundary in which space-charge appears. The study focuses on the plasma potential near plasma boundaries, in low temperature, low pressure plasma in an effort to test this common assumption. To compare potential measurements by both Langmuir probe and emissive probe, plasma potential is also determined by applying inflection point technique to Langmuir probe I-V, as shown in Figure 3. It is generally accepted1 that the plasma potential is found by finding the probe bias voltage at which the second derivative of the current collected differentiated with respect to the bias voltage, 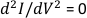figure-introduction-10238, that is, the peak of the dI/dV curve, with respect to the probe bias voltage. Figure 3 demonstrates how this maximum in dI/dV, the inflection point of the current-voltage characteristic, is found.

Langmuir probes (collecting) and emissive probes (emitting) have different I-V characteristics, which also depend on the geometry of the probe tip, as shown in Figure 4. The space-charge effect of the probe must be considered before the probe fabrication. In the experiments, for the planar Langmuir probes, we used a ¼" planar Tantalum disk. We could collect more current and get bigger signals with a larger disk. However, in order for the analyses above to apply, the area of the probe, Ap must be kept smaller than the electron loss area of the chamber, Aw, satisfying21 the inequality 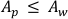figure-introduction-11299. For the cylindrical Langmuir probe, we used a 0.025 mm thick, 1 cm long Tungsten wire for the cylindrical Langmuir probe and a same thickness for the Tungsten wire for the emissive probe. It is important to note that for cylindrical Langmuir probes, for the plasma parameters of these experiments, the radius of the probe tip, rp, is much smaller than its length, Lp, and smaller than the Debye length, λD; that is, 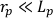figure-introduction-11852, and figure-introduction-11928. 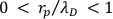In this range of parameters, applying Orbital Motion Limited theory and Laframboise’s development of it22 for the case of thermal electrons and ions, we find that for probe bias voltages equal to or greater than the plasma potential, the electron current collected may be parameterized by a function of the form 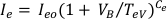figure-introduction-12342, where the exponent figure-introduction-12433. The important point here is that for values of this exponent less than unity, the inflection point method for determining the plasma potential, as described in the paragraph above, applies to cylindrical Langmuir probes too.

Protocol

1. Building Langmuir probes and Emissive probes to fit into a vacuum chamber

  1. Planar Langmuir probe (see Figure 5 for more details)
    1. Take a ¼” diameter stainless steel tube as the probe shaft and bend one end to the desired 90° angle.
    2. Cut the unbent side to a length so that the probe can axially cover more than half of the chamber length.
    3. Fit the unbent side of the shaft through the brass tube by a SS-4-UT-A-8 adapter in combination with a B-810-6 union tube fitting.
    4. Use a ½” brass tube extending out of the customized flanges through a B-810-1-OR swagelok interface to provide axial support for the probe shaft.
    5. Connect the unbent end of the probe shaft to the BNC housing through a B-400-1-OR swagelok fitting, as shown in Figure 6.
    6. Fit the gold-coated nickel wire through two single-bore alumina tubes (1/8” and 3/16” in diameter) with the thicker one fits inside the probe shaft, as shown in Figure 7.
    7. Spot weld one end of gold-coated nickel wire onto a piece of stripped wire, which is soldered onto the pin of the BNC feedthrough at the end of the probe shaft.
    8. Cut the gold-coated wire to length such that the joint with the stripped wire fits inside the alumina tube to prevent short circuit with the probe shaft.
    9. Punch through a tantalum sheet to make a planar Langmuir probe tip (¼” in diameter)
    10. Spot weld the other end of the gold-coated nickel wire onto the edge of the probe tip and set the probe tip to be normal to the axis of the boundary plate.
    11. Position the probe tip a little forward so that the body of the probe does not touch the boundary plate while taking measurements inside the sheath.
    12. Seal all joints with ceramic paste (e.g., Sauereisen Cement No. 31) to insulate the probe circuit components from plasma. Use a heat gun to bake the ceramic joints for 5-10 min.
    13. Use a multimeter to measure the resistance between the probe tip and the BNC connector. If continuity is demonstrated, the probe is ready to be put into the vacuum chamber.
  2. Building a cylindrical emissive probe (see Figure 8 for more details)
    1. Follow step 1.1.1-1.1.4 and repeat step 1.1.5-1.1.7 on the same probe shaft twice with the exception of using a 1/8”, two-bore alumina tube instead of a single-bore one.
    2. Cut the 0.025 mm diameter tungsten wire to about 1 cm.
    3. Spot weld the tungsten filament onto gold-coated wires.
    4. Seal all the joints with ceramic paste and make sure the ceramic paste does not get onto the tungsten filament.
    5. Check continuity between two BNC ends.

2. Generate plasma

  1. Turn on the ion gauge to check the base pressure before putting gas into the chamber. Proceed with zeroing of the baratron gauge if the pressure is in the low 10-6 Torr range. Otherwise, check the leak in the system. The positions of needle valve and the shut off value are open and closed, respectively. 
  2. Use a plastic screwdriver to calibrate the baratron display until the number floats between ±0.01 mTorr.
  3. Close the needle valve so that it is gently seated in a closed position.
  4. Open the shutoff valve. Check that there is no pressure change on the baratron reading.
  5. Slowly turn the knob of the needle valve to release the gas into the chamber until the pressure reaches the requirement for the experiment. The typical working pressure stem from 10-5 ~ 2 x 10-3 Torr. Working gases have included argon, xenon, krypton, oxygen etc.
  6. Turn on the KEPCO voltage power supply and set the voltage to -60 Volts to provide sufficient electron energy for the maximum ionization cross section of argon. Turn on the heating power supply for the filaments and slowly adjust the level until the discharge current reads the required value. The discharge current tends to drop quickly in the first few minutes. Keep adjusting the current level for about 30 minutes until the discharge stabilizes
  7. Connect the voltage supply to the boundary plate and adjust the bias to desired level.

3. Take measurements

NOTE: I-V traces for Langmuir probes and emissive probes are acquired by a 16-bit DAQ board controlled by a Labview program. The details are not presented here since different users have different preferences for taking the data. However, there is a protocol for how to use the probes.

  1. Take the load line: obtain an I-V trace without any plasma discharge in the chamber with all connections made between the probe and its measuring circuit (see Figure 9, Figure 10 & Figure 11 for the UW-Madison and the USD setup).
  2. Langmuir probes
    1. Clean the probe tip (this step is critical, as a clean probe exhibits a sharper ‘knee’ than a dirty probe) by biasing the probe positively to collect a large electron current.
      1. Draw a current through the probe with a variable power supply and 50 Ohms to the machine ground to heat the tip so as to evaporate the layer of impurities that immediately attaches to the probe surface in the plasma and increase the surface resistivity of the probe.
      2. Slowly increase the bias positively to surpass the plasma potential, permitting the probe to begin to draw the electron saturation current.
      3. Continue to raise the potential; once one sees the probe tip glowing cherry red, the probe is clean. It is necessary to have a view of the probe tip in the plasma through a vacuum viewport.
      4. Be careful and vigilant while varying the bias on the probe. If the probe is allowed to get too hot, the probe tip itself could become warped, and worse things can happen, such as the tip could have holes in it, it could evaporate, it could fall off; wires could melt and lose their insulation, and so forth.
      5. Attach the probe to the data acquisition and control circuit (this is the part that will vary from lab to lab), and proceed to sweep the voltage applied to the probe while simultaneously measuring the current drawn by the probe. Save the I-V trace.
    2. Attach the probe to the data acquisition and control circuit (this is the part that will vary from lab to lab), and proceed to sweep the voltage applied to the probe while simultaneously measuring the current drawn by the probe. Save the I-V trace.
  3. Emissive probes
    1. Repeat step 3.2.2 with the emissive probe’s data acquisition and control circuit.

4. Data analysis

  1. Langmuir Probes (See Figure 12, Figure 13 for more details).
    1. Subtract the load line from the total I-V characteristic.
    2. Fit the ion saturation current and subtract from the remaining I-V characteristics.
    3. Take the natural log of current and plot it against the probe voltage.
    4. Take linear fits of transitional region and saturation current separately.
    5. Take the inverse of the slope of the transitional region and obtain the electron temperature value.
    6. Obtain the plasma density by plugging the current at the crossing where the two fitted lines cross each other into Eq.3.
    7. Apply the inflection point technique to the Langmuir probe trace and determine the plasma potential.
  2. Emissive Probe (refer to Figure 2).
    1. Repeat step 4.1.1-4.1.2 for individual I-V characteristics, then smooth each trace.
    2. Differentiate each I-V trace and apply appropriate smoothing.
    3. Locate the peak of each smoothed dI/dV (inflection point).
    4. Apply a linear fit to the inflection points.
    5. Obtain the plasma potential by locating the zero crossing of the fitted line.

Results

Langmuir probes, known to be sensitive to flows and to the kinetic energy of the particles they collect, have up till now have been considered to yield valid measurement of the plasma potential, except in sheaths. But direct comparisons of plasma potentials measured by Langmuir probes and emissive probes have demonstrated that in the quasineutral presheath region of the plasma immediately in contact with the sheath on the plasma side, Langmuir probes do not provide accurate measurements of the plasma potential

Discussion

Langmuir probes are used for particle flux measurements in an extraordinarily wide range of plasma densities and temperatures, from space plasmas in which the electron density is just a few particles 106 m-3 to the edge region of fusion plasmas where the electron density is more like a few times 1020 m-3. Moreover, electron temperatures between 0.1 and a few hundred eV’s have been diagnosed with Langmuir probes. Langmuir probes are often used to measure plasma density and...

Disclosures

The authors have nothing to disclose.

Acknowledgements

This work was partially funded by the U.S. Department of Energy (DOE), through grantDE-SC00114226, and the National Science Foundation through grants PHY-1464741, PHY-1464838, PHY-1804654, and PHY-1804240

Tribute to Noah Hershkowitz:
Noah Hershkowitz made groundbreaking contributions to plasma physics while earning the respect and admiration of his colleagues and students, both as a scientist and a human being.  “Physics,” he once explained, “is like a jigsaw puzzle that’s really old. All the pieces are worn down. Their edges are messed up. Some of the pieces have been put together in the wrong way. They sort of fit, but they’re not actually in the right places. The game is to put them together the right way to find out how the world works.  He died on November 13, 2020, at age 79.

Materials

NameCompanyCatalog NumberComments
0.001" thick tungsten wireMidwest Tungsten Service0.001"Emissive probe filament
0.005" thick tantalum sheetMidwest Tungsten Service0.005"Heating filament to generate plasma
1/2" Brass supprting tube
1/4" Brass Ferrule SetSwagelokB-400-SETInterface between stainless probe shaft and swagelok tube fitting
1/4" OD 304 or 315 stainless steel tubeSwagelokSS-T4-S-035-20Used to make the probe shaft, order seamless, sold in 20' lengths
Alumina tubesCOORSTEK65655, single bore 0.156" OD 0.094 IDsingle bore, double bore, quadruple bore, use for support structure for both emissive and Langmuir probes between the probe tip and shaft
Baratron gaugeMKSType 127Display the pressure when there's gas flowing in the chamber
Brass Swagelok Tube FittingSwagelokB-400-1-ORTube fittings used on the probe
Brass Swagelok Tube FittingSwagelokB-810-6Tube fittings used on the probe
Brass Swagelok Tube FittingSwagelokB-810-1-ORTube fittings used on the probe
Ceramic liquidSauereisenNo. 31 Ceramic Encapsulant LiquidMix with No.31 cement power to make the ceramic paste
Ceramic powderSauereisenCement Powder No. 31 Off-WhiteThere are Saureisen cements that cure with water, e.g. No.10 Powder
Gold plated nickel wireSYLVANIA ELECTRIC PRODUCTspod-welded to the probe tip to provide supports
Ion gauge controllerGranville-Phillips270 Gauge controllerHeat up the ion gauge and display pressure inside the chamber
Mechanical pumpLeybold D60 D60ACD60 D60ACBring the pressure down to ~10 mTorr then serve as the backing pump for the turbo pump
needle valveWhiteySS-22RS4Metering Micro-Needle Micrometer Valve 1/4" Tube Swagelok fittings
Power supplyKepcoATE 100-10MVoltage Bias supply of heating filament
Power supplySorensenDCR 20-115BHeating supply of heating filament
shutoff valveKurt J. LeskerNupro SS-4BKKnob handle, for 1/4" tubing, swagelok fittings
Stainless Steel Ultra-Torr Vacuum FittingSwagelokSS-4-UT-A-8Tube fittings used on the probe
Teflon coated wireGeyer SystemsP31546Connect the gold-coated wire to BNC pin
Turbo pumpPFEIFFERTPH 240 CBring the pressure down to 1E-6 Torr
Vacuum greaseAPIEZONL Ultra High Vacuum Grade GreaseVacuum grease used to lubricate the oring
Viton OringsGrainger#031Round #031 Medium Hard Viton O-Ring, 1.739" I.D., 1.879" O.D
Viton OringsGrainger#010Round #010 Medium Hard Viton O-Ring, 0.239" I.D., 0.379"O.D

References

  1. Godyak, V. A., Alexandrovich, B. M. Comparative analyses of plasma probe diagnostics techniques. Journal of Applied Physics. 118, 233302 (2015).
  2. Gurnett, D. A., et al. The Cassini Radio and Plasma wave investigation. Space Science Reviews. 114, 395-463 (2004).
  3. Olson, J., Brenning, N., Wahlund, J. E., Gunell, H. On the interpretation of Langmuir probe data inside a spacecraft sheath. Review of Scientific Instruments. 81, 105106 (2010).
  4. Lebreton, J. P., et al. The ISL Langmuir probe experiment processing onboard DEMETER: Scientific objectives, description and first results. Planetary and Space Science. 54, 472-486 (2006).
  5. Godyak, V. A., Piejak, R. B., Alexandrovich, B. M. Measurements of electron energy distribution in low-pressure RF discharges. Plasma Sources Science and Technology. 1, 36-58 (1992).
  6. You, K. H., et al. Experimental and computational investigations of the effect of the electrode gap on capacitively coupled radio frequency oxygen discharges. Physics of Plasmas. 26, 013503 (2019).
  7. Sobolewski, M. A., Kim, J. H. The effects of radio-frequency bias on electron density in an inductively coupled plasma reactor. Journal of Applied Physics. 102 (11), 113302 (2007).
  8. Godyak, V. A., Piejak, R. B., Alexandrovich, B. M. Electron energy distribution function measurements and plasma parameters in inductively coupled argon plasma. Plasma Sources Science and Technology. 11, 525-543 (2002).
  9. Leonard, A. W. Plasma detachment in divertor tokamaks. Plasma Physics and Controlled Fusion. 60, 044001 (2018).
  10. Loarte, A., et al. Plasma detachment in JET Mark I divertor experiments. Nuclear Fusion. 38, 331-371 (1998).
  11. Matthews, G. F. Tokamak plasma diagnosis by electrical probes. Plasma Physics and Controlled Fusion. 36, 1595-1628 (1994).
  12. Langmuir, I. The pressure effect and other phenomena in gaseous discharges. Journal of the Franklin Institute. 196, 751-762 (1923).
  13. Hutchinson, I. H. . Principles of Plasma Diagnostics. 2nd. Ed. , (2002).
  14. Hershkowitz, N., Auciello, N., Flamm, D. L. How Langmuir Probes Work. Plasma Diagnostics Volume 1 Discharge Parameters and Chemistry. , 114 (1989).
  15. Lee, H. C., Lee, J. K., Chung, W. C. Evolution of the electron energy distribution and E-H mode transition in inductively coupled nitrogen plasma. Physics of Plasmas. 17, 033506 (2010).
  16. Amemiya, H. Plasmas with negative ions-probe measurements and charge equilibrium. Journal of Physics D: Applied Physics. 23, 999 (1990).
  17. Andreu, J., Sardin, G., Esteve, J., Morenza, J. L. Filament discharge plasma of argon with electrostatic confinement. Journal of Physics D: Applied Physics. 18, 1339-1345 (1985).
  18. Bohm, D., Guthrie, A., Wakering, R. K. Minimum Kinetic Energy Requirement for a Stable Sheath. The Characteristics of Electrical Discharges in Magnetic Fields. , (1949).
  19. Chen, F. F. . Introduction to Plasma Physics and Controlled Fusion, 3rd Ed. , (2016).
  20. Sheehan, J. P., Hershkowitz, N. Emissive probes. Plasma Sources Science and Technology. 20, 063001 (2011).
  21. Barnat, E. V., Laity, G. R., Baalrud, S. D. Response of the plasma to the size of an anode electrode biased near the plasma potential. Physics of Plasmas. 21, 103512 (2014).
  22. Mausbach, M. Parametrization of the Laframboise theory for cylindrical Langmuir probe analysis. Journal of Vacuum Science and Technology A. 15, 2923-2929 (1997).
  23. Li, P., Hershkowitz, N., Wackerbarth, E., Severn, G. Experimental studies of the difference between plasma potentials measured by Langmuir probes and emissive probes in presheaths. Plasma Sources Science and Technology. 29, 025015 (2020).
  24. Goeckner, M. J., Goree, J., Sheridan, T. E. Measurements of ion velocity and density in the plasma sheath. Physics of Fluids B: Plasma Physics. 4, 1663 (1992).
  25. Lee, D., Hershkowitz, N., Severn, G. D. Measurements of Ar+ and Xe+ velocities near the sheath boundary of Ar-Xe plasma using two diode lasers. Applied Physics Letters. 91, 041505 (2007).
  26. Yan, S., Kamal, H., Amundson, J., Hershkowitz, N. Use of emissive probes in high pressure plasma. Review of Scientific Instruments. 67 (12), 4130-4137 (1996).
  27. Smith, J. R., Hershkowitz, N., Coakley, P. Inflection-point method of interpreting emissive probe characteristics. Review of Scientific Instruments. 50, 210-218 (1979).
  28. Campanell, M. D., Umansky, M. V. Strongly Emitting Surfaces Unable to Float below Plasma Potential. Physical Review Letters. 116, 085003 (2016).
  29. Kraus, B. F., Raitses, Y. Floating potential of emitting surfaces in plasmas with respect to the space potential. Physics of Plasmas. 25, 030701 (2018).
  30. Yip, C. -. S., Jin, C., Zhang, W., Xu, G. S., Hershkowitz, N. Experimental investigation of sheath effects on I-V traces of strongly electron emitting probes. Plasma Sources Science and Technology. 29, 025025 (2020).

Reprints and Permissions

Request permission to reuse the text or figures of this JoVE article

Request Permission

Explore More Articles

Langmuir ProbesEmissive ProbesPlasma Potential MeasurementsLow Pressure PlasmasVacuum TechniquesElectrostatic ProbesLab MaterialsDiagnosticsProbe ConstructionCeramic PasteStainless Steel TubeBNC HousingNickel WireAlumina TubesTantalum SheetResistance Measurement

This article has been published

Video Coming Soon

JoVE Logo

Privacy

Terms of Use

Policies

Contact Us

Recommend to library

JoVE NEWSLETTERS

Research

Education

Authors

Librarians

ABOUT JoVE

Copyright © 2025 MyJoVE Corporation. All rights reserved